2022-2023学年江苏省兴化市七年级数学第二学期期末监测模拟试题含答案

2022-2023学年江苏省兴化市七年级数学第二学期期末监测模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项:

1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题(每小题3分,共30分)

1．如图，将直径为2cm的半圆水平向左平移2cm，则半圆所扫过的面积（阴影部分）为（　　）

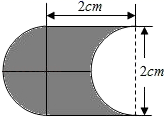
A．πcm2 B．4 cm2 C．cm2 D．cm2

2．已知点A（x1，y1），B（x2，y2），C（x3，y3）都在反比例函数的图象上，且x1＜x2＜x3，（     ）

A．若＜＜，则++＞0 B．若＜＜，则＜0

C．若＜＜，则++＞0 D．若＜＜，则＜0

3．下列长度的三根木棒首尾顺次连接，能组成直角三角形的是（   ）

A．1，2，3 B．4，6，8 C．6，8，10 D．13，14，15

4．对于一次函数y＝﹣2x+4，下列结论错误的是(   )

A．函数的图象不经过第三象限

B．函数的图象与x轴的交点坐标是(2，0)

C．函数的图象向下平移4个单位长度得y＝﹣2x的图象

D．若两点A(x1，y1)，B(x2，y2)在该函数图象上，且x1＜x2，则y1＜y2

5．如果关于x的不等式（a1）x2的解集为x1，则a的值是（    ）．

A．a3 B．a3 C．a3 D．a3

6．计算的结果是（　　）

A．﹣2 B．﹣1 C．1 D．2

7．用配方法解下列方程，其中应在方程左右两边同时加上4的是（　　）

A．x2﹣2x＝5 B．x2+4x＝5 C．2x2﹣4x＝5 D．4x2+4x＝5

8．如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=15，则S2的值是(     )

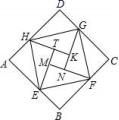
A．3 B． C．5 D．

9．现有甲、乙两个合唱队，队员的平均身高都是175cm，方差分别为，，那么两个队中队员的身高较整齐的是（    ）

A．甲队 B．乙队 C．两队一样高 D．不能确定

10．若从边形的一个顶点出发，最多可以作3条对角线，则该边形的内角和是（    ）

A． B． C． D．

二、填空题(本大题共有6小题，每小题3分，共18分)

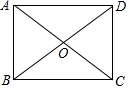
11．如图，矩形ABCD中，对角线AC与BD相交于点O，AB＝3，BC＝4，则△AOB的周长为_____．

12．妈妈做了一份美味可口的菜品，为了了解菜品的咸淡是否适合，于是妈妈取了一点品尝，这应该属于___________（填普查或抽样调查）

13．如图，直线（＞0）与轴交于点（-1,0），关于的不等式＞0的解集是_____________．

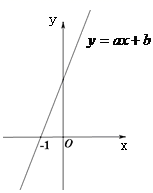
14．直线与轴的交点坐标是________________.

15．对于一个函数，如果它的自变量 x 与函数值 y 满足：当−1≤x≤1 时，−1≤y≤1，则称这个函数为“闭 函数”.例如：y=x，y=−x 均是“闭函数”.  已知 y  ax2 bx  c(a0) 是“闭函数”，且抛物线经过点 A(1，−1)和点 B(−1，1)，则 a 的取值范围是______________.

16．如图，在□ABCD中，对角线AC、BD相交于O，AC＋BD＝10，BC＝3，则△AOD的周长为       ．

三、解下列各题(本大题共8小题，共72分)

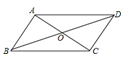
17．（8分）如图,在平行四边形中，点、分别是、上的点，且，，求证：

（1）；

（2）四边形是菱形.

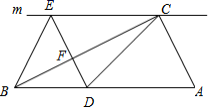
18．（8分）如图，在中，，过点的直线，为边上一点，过点作交直线于点，垂足为点，连结、．

（1）求证：；

（2）当点是中点时，四边形是什么特殊四边形？说明你的理由；

（3）若点是中点，当四边形是正方形时，则大小满足什么条件？

19．（8分）2019年4月25日至27日，第二届“一带一路”国际合作高峰论坛在北京举行，本届论坛期间，中国同30多个国家签署经贸合作协议。我国准备将地的茶叶1000吨和地的茶叶500吨销往“一带一路”沿线的地和地，地和地对茶叶需求分别为900吨和600吨，已知从、两地运茶叶到、两地的运费（元/吨）如下表所示，设地运到地的茶叶为吨，

（1）用含的代数式填空：地运往地的茶叶吨数为___________，地运往地的茶叶吨数为___________，地运往地的茶叶吨数为___________.

（2）用含（吨）的代数式表示总运费（元），并直接写出自变量的取值范围；

（3）求最低总运费，并说明总运费最低时的运送方案.

20．（8分）如图，是等边三角形，是中线，延长至，.

（1）求证：；

（2）请在图中过点作交于，若，求的周长.

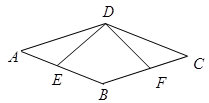
21．（8分）如图，点E、F分别是▱ABCD的边BC、AD上的点，且BE=DF．

（1）试判断四边形AECF的形状；

（2）若AE=BE，∠BAC=90°，求证：四边形AECF是菱形．

22．（10分）我们知道平行四边形有很多性质，现在如果我们把平行四边形沿着它的一条对角线翻折，会发现这其中还有更多的结论．

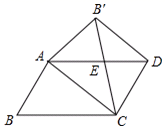
（发现与证明）▱ABCD中，AB≠BC，将△ABC沿AC翻折至△AB`C，连结B`D．

结论1：△AB`C与▱ABCD重叠部分的图形是等腰三角形；结论2：B`D∥AC；

（1）请证明结论1和结论2；

（应用与探究）

（2）在▱ABCD中，已知BC=2，∠B=45°，将△ABC沿AC翻折至△AB`C，连接B`D若以A、C、D、B`为顶点的四边形是正方形，求AC的长（要求画出图形）

23．（10分）当在什么范围内取值时，关于的一元一次方程的解满足？

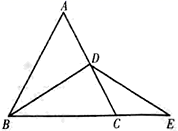
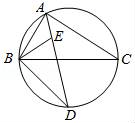
24．（12分）如图，∠BAC的平分线交△ABC的外接圆于点D，∠ABC的平分线交AD于点E．

（1）求证：DE＝DB；

（2）若∠BAC＝90°，BD＝4，求△ABC外接圆的半径．

参考答案

一、选择题(每小题3分,共30分)

1、B

2、B

3、C

4、D

5、C

6、C

7、B

8、C

9、B

10、B

二、填空题(本大题共有6小题，每小题3分，共18分)

11、1

12、抽样调查

13、x＞-1

14、

15、或

16、8

三、解下列各题(本大题共8小题，共72分)

17、 (1)证明见解析；（2）证明见解析．

18、（1）见解析  （2）见解析   （3）

19、（1），，；（2）；（3）由地运往地400吨，运往地600吨；由地运往地500吨时运费最低

20、（1）详见解析；（2）48.

21、（1）四边形AECF为平行四边形；（2）见解析

22、

23、

24、 (1)证明见解析(2)2