


2022-2023学年广东省广州市部分区及学校七下数学期末学业质量监测试题含答案
展开2022-2023学年广东省广州市部分区及学校七下数学期末学业质量监测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1.有100个数据,落在某一小组内的频数与总数之比是0.4,那么在这100个数据中,落在这一小组内的数据的频数是( )
A.100 B.40 C.20 D.4
2.函数![]() 与
与![]() (
(![]() )在同一平面直角坐标系内的图象可能是( )
)在同一平面直角坐标系内的图象可能是( )
A.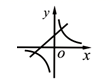 B.
B.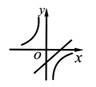 C.
C.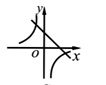 D.
D.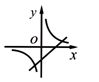
3.下列代数式是分式的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.学校举行演讲比赛,共有15名同学进入决赛,比赛将评出金奖1名,银奖3名,铜奖4名,某选手知道自己的分数后,要判断自己能否获奖,他应当关注有关成绩的( )
A.平均数 B.中位数 C.众数 D.方差
5.使代数式![]() 有意义的x的取值范围( )
有意义的x的取值范围( )
A.x>2 B.x≥2 C.x>3 D.x≥2且x≠3
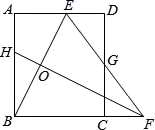
6.如图,已知线段AB=12,点M、N是线段AB上的两点,且AM=BN=2,点P是线段MN上的动点,分别以线段AP、BP为边在AB的同侧作正方形APDC、正方形PBFE,点G、H分别是CD、EF的中点,点O是GH的中点,当P点从M点到N点运动过程中,OM+OB的最小值是( )
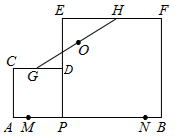
A.10 B.12 C.2 ![]() D.12
D.12![]()
7.下列选择中,是直角三角形的三边长的是( )
A.1,2,3 B.2,5,3 C.3,4,5 D.4,5,6
8.已知四边形 ABCD ,有以下四个条件:① AB ∥ CD ;② BC ∥ AD ;③ AB CD ;④ABC ADC .从这四个条件中任选两个,能使四边形 ABCD 成为平行四边形的选法有( )
A.3 种 B.4 种 C.5 种 D.6 种
9.正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )
A. B.
B. C.
C.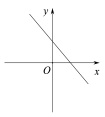 D.
D.
10.中国自主研发的第一台7纳米刻蚀机,是芯片制造和微观加工最核心的设备之一,7纳米就是0.000000007米,数据0.000000007用科学记数法表示为( )
A.0.7×10-8 B.7×10-8 C.7×10-9 D.7×10-10
二、填空题(本大题共有6小题,每小题3分,共18分)
11.已知x+y=﹣1,xy=3,则x2y+xy2=_____.
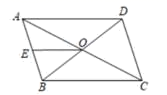
12.如图,在□ABCD中,对角线AC和BD交于点O,点E为AB边上的中点,OE=2.5cm,则AD=________cm。
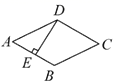
13.如图,菱形ABCD的边长是4 cm,E是AB的中点,且DE⊥AB,则菱形ABCD的面积为__________.
14.如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,则BC的长是___.
15.一组数据-3,x,-2,3,1,6的中位数是1,则其方差为________
16.因式分解:![]() ____.
____.
三、解下列各题(本大题共8小题,共72分)
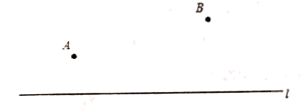
17.(8分)用圆规、直尺作图,不写作法,但要保留作图痕迹.
如图,已知点![]() ,点
,点![]() 和直线
和直线![]() .
.
(1)在直线![]() 上求作一点
上求作一点![]() ,使
,使![]() 最短;
最短;
(2)请在直线![]() 上任取一点
上任取一点![]() (点
(点![]() 与点
与点![]() 不重合),连接
不重合),连接![]() 和
和![]() ,试说明
,试说明![]() .
.
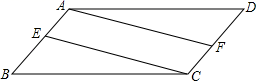
18.(8分)如图,在▱ABCD中,E,F分别是边AB,CD的中点,求证:AF=CE.
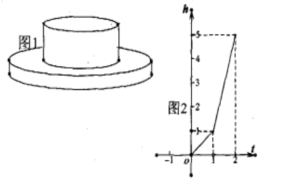
19.(8分)如图1是一个有两个圆柱形构成的容器,最下面的圆柱形底面半径![]() 。匀速地向空容器内注水,水面高度
。匀速地向空容器内注水,水面高度![]() (单位:米)与时间
(单位:米)与时间![]() (单位:小时)的关系如图2所示。
(单位:小时)的关系如图2所示。
(1)求水面高度![]() 与时间
与时间![]() 的函数关系式;
的函数关系式;
(2)求注水的速度(单位:立方米/每小时),并求容器内水的体积![]() 与注水时间
与注水时间![]() 的函数关系式;
的函数关系式;
(3)求上面圆柱的底面半径(壁厚忽略不计)。
20.(8分)在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,5×5正方形方格纸图中,点A,B都在格点处.
(1)请在图中作等腰△ABC,使其底边AC=2![]() ,且点C为格点;
,且点C为格点;
(2)在(1)的条件下,作出平行四边形ABDC,且D为格点,并直接写出平行四边形ABDC的面积.
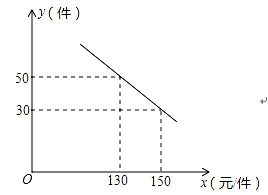
21.(8分)电商时代使得网购更加便捷和普及.小张响应国家号召,自主创业,开了家淘宝店.他购进一种成本为100元/件的新商品,在试销中发现:销售单价x(元)与每天销售量y(件)之间满足如图所示的关系.
(1)求y与x之间的函数关系式;
(2)若某天小张销售该产品获得的利润为1200元,求销售单价x的值.
22.(10分)已知关于x的方程x2-6x+m2-3m-5=0一个根是-1,求方程的另一个根和m的值.
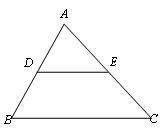
23.(10分)已知:D,E分别为△ABC的边AB,AC的中点.求证:DE∥BC,且DE=![]() BC
BC
24.(12分)我市从 2018 年 1 月 1 日开始,禁止燃油助力车上路,于是电动自 行车的市场需求量日渐增多.某商店计划最多投入 8 万元购进 A、B 两种型号的 电动自行车共 30 辆,其中每辆 B 型电动自行车比每辆 A 型电动自行车多 500 元.用 5 万元购进的 A 型电动自行车与用 6 万元购进的 B 型电动自行车数量一 样.
(1)求 A、B 两种型号电动自行车的进货单价;
(2)若 A 型电动自行车每辆售价为 2800 元,B 型电动自行车每辆售价为 3500 元,设该商店计划购进 A 型电动自行车 m 辆,两种型号的电动自行车全部销售 后可获利润 y 元.写出 y 与 m 之间的函数关系式;
(3)该商店如何进货才能获得最大利润;此时最大利润是多少元.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、D
3、D
4、B
5、D
6、C
7、C
8、B
9、A
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、-1
12、5
13、8![]()
14、7
15、9
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)作图见解析;(2)证明见解析
18、见解析.
19、(1)![]() ;(2)
;(2)![]() ;(3)4
;(3)4
20、 (1)见解析;(2)画图见解析;其面积为8.
21、(1)y=−x+180;(2)120元或160元;
22、方程的另一根是2,m=3或m=3;
23、证明见解析
24、(1)A、B 两种型号电动自行车的进货单价分别为 2500 元 3000 元;(2)y=﹣200m+15000(20≤m≤30);(3)m=20 时,y 有最大值,最大值为 11000 元.
2023-2024学年广东省广州市部分区及学校九上数学期末学业水平测试试题含答案: 这是一份2023-2024学年广东省广州市部分区及学校九上数学期末学业水平测试试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,方程的根为等内容,欢迎下载使用。
广东省深圳市龙岗区石芽岭学校2022-2023学年七下数学期末学业质量监测模拟试题含答案: 这是一份广东省深圳市龙岗区石芽岭学校2022-2023学年七下数学期末学业质量监测模拟试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
广东省广州市南沙区博海学校2022-2023学年七下数学期末监测试题含答案: 这是一份广东省广州市南沙区博海学校2022-2023学年七下数学期末监测试题含答案,共6页。试卷主要包含了一次函数的图象不经过象限,下列说法等内容,欢迎下载使用。












