


2022-2023学年天津市宁河县芦台五中七下数学期末达标检测试题含答案
展开
这是一份2022-2023学年天津市宁河县芦台五中七下数学期末达标检测试题含答案,共7页。
2022-2023学年天津市宁河县芦台五中七下数学期末达标检测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.A、B两点在一次函数图象上的位置如图所示,两点的坐标分别是![]() ,
,![]() ,下列结论正确的是
,下列结论正确的是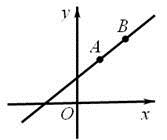 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 2.两次小测验中,李红分别得了64分(满分80分)和82分(满分100分),如果都按满分100分计算,李红两次成绩的平均分为( )A.73 B.81 C.64.8 D.803.在▱ABCD中,∠C=32°,则∠A的度数为( )A.148° B.128° C.138° D.32°4.若a,b,c满足
2.两次小测验中,李红分别得了64分(满分80分)和82分(满分100分),如果都按满分100分计算,李红两次成绩的平均分为( )A.73 B.81 C.64.8 D.803.在▱ABCD中,∠C=32°,则∠A的度数为( )A.148° B.128° C.138° D.32°4.若a,b,c满足![]() 则关于x的方程
则关于x的方程![]() 的解是( )A.1,0 B.-1,0 C.1,-1 D.无实数根5.《九章算术》中的“折竹抵地”问题上:今有竹高一丈,末折抵地,去本六尺。问折高几何?意思是:如图,一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远。问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
的解是( )A.1,0 B.-1,0 C.1,-1 D.无实数根5.《九章算术》中的“折竹抵地”问题上:今有竹高一丈,末折抵地,去本六尺。问折高几何?意思是:如图,一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远。问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( ) A.
A. ![]() B.
B. ![]() C.x2+6=(10-x)2 D.x2+62=(10-x)26.2022年将在北京﹣张家口举办冬季奥运会,北京将成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市.某队要从两名选手中选取一名参加比赛,为此对这两名队员进行了五次测试,测试成绩如图所示:则下列说法中正确的是( )
C.x2+6=(10-x)2 D.x2+62=(10-x)26.2022年将在北京﹣张家口举办冬季奥运会,北京将成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市.某队要从两名选手中选取一名参加比赛,为此对这两名队员进行了五次测试,测试成绩如图所示:则下列说法中正确的是( )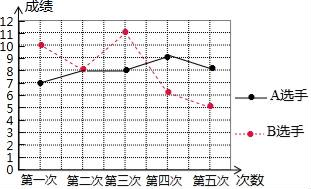 A.SA2>SB2,应该选取B选手参加比赛B.SA2<SB2,应该选取A选手参加比赛C.SA2≥SB2,应该选取B选手参加比赛D.SA2≤SB2,应该选取A选手参加比赛7.等式
A.SA2>SB2,应该选取B选手参加比赛B.SA2<SB2,应该选取A选手参加比赛C.SA2≥SB2,应该选取B选手参加比赛D.SA2≤SB2,应该选取A选手参加比赛7.等式![]() •
•![]() =
=![]() 成立的条件是( )A.
成立的条件是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 8.已知:如图①,长方形ABCD中,E是边AD上一点,且AE=6cm,点P从B出发,沿折线BE-ED-DC匀速运动,运动到点C停止.P的运动速度为2cm/s,运动时间为t(s),△BPC的面积为y(cm2),y与t的函数关系图象如图②,则下列结论正确的有( )①a=7 ②AB=8cm ③b=10 ④当t=10s时,y=12cm2
8.已知:如图①,长方形ABCD中,E是边AD上一点,且AE=6cm,点P从B出发,沿折线BE-ED-DC匀速运动,运动到点C停止.P的运动速度为2cm/s,运动时间为t(s),△BPC的面积为y(cm2),y与t的函数关系图象如图②,则下列结论正确的有( )①a=7 ②AB=8cm ③b=10 ④当t=10s时,y=12cm2 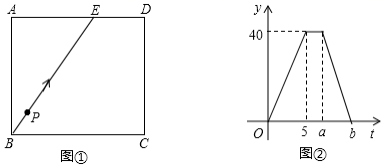 A.1个 B.2个 C.3个 D.4个9.下面的图形是天气预报的图标,其中既是轴对称图形又是中心对称图形的是( )A.
A.1个 B.2个 C.3个 D.4个9.下面的图形是天气预报的图标,其中既是轴对称图形又是中心对称图形的是( )A. B.
B. C.
C. D.
D. 10.直角三角形斜边上的高与中线分别为 5cm 和 6cm,则它的面积为( )cm1.A.30 B.60 C.45 D.1511.已知不等式ax+b>0的解集是x<-2,则函数y=ax+b的图象可能是( )A.
10.直角三角形斜边上的高与中线分别为 5cm 和 6cm,则它的面积为( )cm1.A.30 B.60 C.45 D.1511.已知不等式ax+b>0的解集是x<-2,则函数y=ax+b的图象可能是( )A.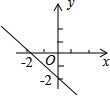 B.
B.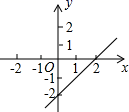 C.
C.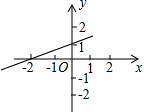 D.
D.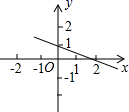 12.约分
12.约分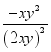 的结果是( )A.
的结果是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(每题4分,满分20分,将答案填在答题纸上)13.当x=4时,二次根式
二、填空题(每题4分,满分20分,将答案填在答题纸上)13.当x=4时,二次根式![]() 的值为______.14.当m=________时,函数y=-(m-2)
的值为______.14.当m=________时,函数y=-(m-2)![]() +(m-4)是关于x的一次函数.15.如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT的长为_____.
+(m-4)是关于x的一次函数.15.如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT的长为_____.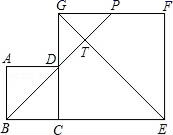 16.一组数据:
16.一组数据:![]() ,则这组数据的方差是__________.17.如图,在坐标系中,有
,则这组数据的方差是__________.17.如图,在坐标系中,有![]() ,且A(﹣1,3),B(﹣3,﹣1),C(﹣3,3),已知
,且A(﹣1,3),B(﹣3,﹣1),C(﹣3,3),已知![]() 是由
是由![]() 旋转得到的.请写出旋转中心的坐标是____,旋转角是____度.
旋转得到的.请写出旋转中心的坐标是____,旋转角是____度.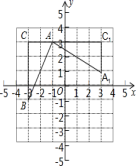 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)阅读下列材料:在因式分解中,把多项式中某些部分看作一个整体,用一个新的字母代替(即换元),不仅可以简化要分解的多项式的结构,而且能使式子的特点更加明显,便于观察如何进行因式分解,我们把这种因式分解的方法称为“换元法”.下面是小涵同学用换元法对多项式(x2﹣4x+1)(x2﹣4x+7)+9进行因式分解的过程.解:设x2﹣4x=y原式=(y+1)(y+7)+9(第一步)=y2+8y+16(第二步)=(y+4)2(第三步)=(x2﹣4x+4)2(第四步)请根据上述材料回答下列问题:(1)小涵同学的解法中,第二步到第三步运用了因式分解的 ;A.提取公因式法 B.平方差公式法 C.完全平方公式法(2)老师说,小涵同学因式分解的结果不彻底,请你写出该因式分解的最后结果: ;(3)请你用换元法对多项式(x2+2x)(x2+2x+2)+1进行因式分解. 19.(5分)某市自来水公司为了鼓励市民节约用水,采取分段收费标准. 若某户居民每月应缴水费y(元)与用水量x(吨)的函数图象如图所示,(1)分别写出x≤5和x>5的函数解析式;(2)观察函数图象,利用函数解析式,回答自来水公司采取的收费标准;(3)若某户居民六月交水费31元,则用水多少吨?
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)阅读下列材料:在因式分解中,把多项式中某些部分看作一个整体,用一个新的字母代替(即换元),不仅可以简化要分解的多项式的结构,而且能使式子的特点更加明显,便于观察如何进行因式分解,我们把这种因式分解的方法称为“换元法”.下面是小涵同学用换元法对多项式(x2﹣4x+1)(x2﹣4x+7)+9进行因式分解的过程.解:设x2﹣4x=y原式=(y+1)(y+7)+9(第一步)=y2+8y+16(第二步)=(y+4)2(第三步)=(x2﹣4x+4)2(第四步)请根据上述材料回答下列问题:(1)小涵同学的解法中,第二步到第三步运用了因式分解的 ;A.提取公因式法 B.平方差公式法 C.完全平方公式法(2)老师说,小涵同学因式分解的结果不彻底,请你写出该因式分解的最后结果: ;(3)请你用换元法对多项式(x2+2x)(x2+2x+2)+1进行因式分解. 19.(5分)某市自来水公司为了鼓励市民节约用水,采取分段收费标准. 若某户居民每月应缴水费y(元)与用水量x(吨)的函数图象如图所示,(1)分别写出x≤5和x>5的函数解析式;(2)观察函数图象,利用函数解析式,回答自来水公司采取的收费标准;(3)若某户居民六月交水费31元,则用水多少吨?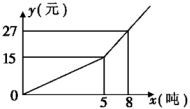 20.(8分)反比例函数
20.(8分)反比例函数![]() 的图像经过
的图像经过![]() 、
、![]() 两点.(1)求m,n的值;(2)根据反比例图像写出当
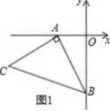
两点.(1)求m,n的值;(2)根据反比例图像写出当![]() 时,y的取值范围. 21.(10分)春节前小王花1200元从农贸市场购进批发价分别为每箱30元与50元的A,B两种水果进行销售,并分别以每箱35元与60元的价格出售,设购进A水果x箱,B水果y箱.(1)让小王将水果全部售出共赚了215元,则小王共购进A、B水果各多少箱?(2)若要求购进A水果的数量不得少于B水果的数量,则应该如何分配购进A, B水果的数量并全部售出才能获得最大利润,此时最大利润是多少? 22.(10分)如图1,
时,y的取值范围. 21.(10分)春节前小王花1200元从农贸市场购进批发价分别为每箱30元与50元的A,B两种水果进行销售,并分别以每箱35元与60元的价格出售,设购进A水果x箱,B水果y箱.(1)让小王将水果全部售出共赚了215元,则小王共购进A、B水果各多少箱?(2)若要求购进A水果的数量不得少于B水果的数量,则应该如何分配购进A, B水果的数量并全部售出才能获得最大利润,此时最大利润是多少? 22.(10分)如图1,![]() ,以
,以![]() 点为顶点、
点为顶点、![]() 为腰在第三象限作等腰
为腰在第三象限作等腰![]() .
.
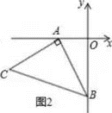 (1)求
(1)求![]() 点的坐标;(2)如图2,在平面内是否存在一点
点的坐标;(2)如图2,在平面内是否存在一点![]() ,使得以
,使得以![]() 为顶点的四边形为平行四边形?若存在,请写出
为顶点的四边形为平行四边形?若存在,请写出![]() 点坐标;若不存在,请说明理由; 23.(12分)解分式方程:(1)
点坐标;若不存在,请说明理由; 23.(12分)解分式方程:(1)![]() ; (2)
; (2)![]() . 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、B2、B3、D4、C5、D6、B7、C8、B9、A10、A11、A12、C 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、014、-215、2
. 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、B2、B3、D4、C5、D6、B7、C8、B9、A10、A11、A12、C 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、014、-215、2 ![]() 16、
16、![]() 17、
17、![]() 1 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)C;(2)(x﹣2)1;(3)(x+1)1.19、 (1)
1 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)C;(2)(x﹣2)1;(3)(x+1)1.19、 (1) ![]() (x≤5),
(x≤5), ![]() (x>5);(2)见解析;(3)9吨.20、(1)
(x>5);(2)见解析;(3)9吨.20、(1)![]() ,
,![]() ;(2)当
;(2)当![]() 时,
时,![]() .21、(1)小王共购进A水果25箱,B水果9箱;(2)应购进A水果15箱、B水果15箱能够获得最大利润,最大利润为225元.22、(1)点
.21、(1)小王共购进A水果25箱,B水果9箱;(2)应购进A水果15箱、B水果15箱能够获得最大利润,最大利润为225元.22、(1)点![]() 的坐标为
的坐标为![]() ;(2)(-4,-6)或(-8,2)或(4,-2).23、(1)
;(2)(-4,-6)或(-8,2)或(4,-2).23、(1)![]() ;(2)原方程无解.
;(2)原方程无解.
相关试卷
这是一份2023-2024学年天津市宁河县芦台五中数学八上期末联考试题含答案,共6页。试卷主要包含了答题时请按要求用笔,的值是,下列表述中,能确定准确位置的是等内容,欢迎下载使用。
这是一份2022-2023学年天津市宁河县名校数学七下期末学业水平测试试题含答案,共7页。
这是一份2022-2023学年天津市重点中学七下数学期末达标检测试题含答案,共7页。









