


2022-2023学年四川省南充市顺庆区数学七年级第二学期期末质量检测模拟试题含答案
展开2022-2023学年四川省南充市顺庆区数学七年级第二学期期末质量检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若正比例函数的图象经过点(2,4),则这个图象也必经过点( )
A.(2,1) B.(﹣1,﹣2) C.(1,﹣2) D.(4,2)
2.对四边形ABCD添加以下条件,使之成为平行四边形,正面的添加不正确的是( )
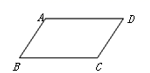
A.AB∥CD,AD=BC B.AB=CD,AB∥CD
C.AB=CD,AD=BC D.AC与BD互相平分
3.已知:以a,b,c为边的三角形满足(a﹣b)(b﹣c)=0,则这个三角形是( )
A.等腰三角形 B.直角三角形
C.等边三角形 D.等腰直角三角形
4.下列等式中,计算正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.下列图形既是中心对称图形又是轴对称图形的是( )
A. B.
B. C.
C. D.
D.
6.已知某一次函数的图象与直线![]() 平行,且过点(3, 7),那么此一次函数为( )
平行,且过点(3, 7),那么此一次函数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.如图,直线![]() 与
与![]() =-x+3相交于点A,若
=-x+3相交于点A,若![]() <
<![]() ,那么( )
,那么( )
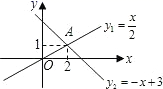
A.x>2 B.x<2 C.x>1 D.x<1
8.生物刘老师对本班50名学生的血型进行了统计,列出如下统计表,则本班O型血的有( )
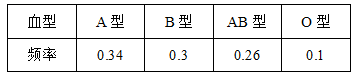
A.17人 B.15人 C.13人 D.5人
9.若样本x1+1,x2+1,…,xn+1的平均数为10,方差为2,则对于样本x1+2,x2+2,…,xn+2,下列结论正确的是( )
A.平均数为10,方差为2 B.平均数为11,方差为3
C.平均数为11,方差为2 D.平均数为12,方差为4
10.如图,在△ABC中,AB=5,AC=3,AD是角平分线,AE是中线,过点C作CG⊥AD于点F,交AB于点G,连接EF,则线段EF的长为( )
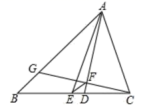
A.![]() B.
B.![]() C.3 D.1
C.3 D.1
11.反比例函数![]() 图象上有三个点
图象上有三个点![]() ,
,![]() ,
,![]() ,若
,若![]() ,则
,则![]() 的大小关系是( )
的大小关系是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.2019年6月19日,重庆轨道十八号线(原5A线)项目加快建设动员大会在项目土建七标段施工现场矩形,预计改线2020年全面建成,届时有效环节主城南部交通拥堵,全线已完成桩点复测,滩子口站到黄桷坪站区间施工通道等9处工点打围,在此过程中,工程队在工作了一段时间后,因雨被迫停工几天,随后工程队加快了施工进度,按时完成了施工通道工点打围。下面能反映该工程施工道路y(米)与时间x(天)的关系的大致图像是( )
A.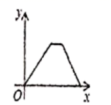 B.
B.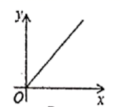 C.
C.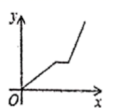 D.
D.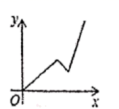
二、填空题(每题4分,满分20分,将答案填在答题纸上)
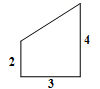
13.在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、3、4,则原直角三角形纸片的斜边长是 .
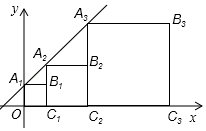
14.正方形A1B1C1O,A2B2C2C1,A3B3C3C2……按如图所示放置,点A1、A2、A3……在直线y=x+1上,点C1、C2、C3……在x轴上,则A2019的坐标是___.
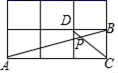
15.如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB,CD相交于点P,则△PBD与△PAC的面积比为_____.
16.中美贸易战以来,强国需更多的中国制造,中芯国际扛起中国芯片大旗,目前我国能制造芯片的最小工艺水平已经达到7纳米,居世界前列,已知1纳米=0.000000001米,用料学记数法将7纳米表示为______米.
17.菱形的两条对角线的长分别为6和8,则这个菱形的周长为_____.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)已知一条直线AB经过点(1,4)和(-1,-2)
(1)求直线AB的解析式.
(2)求直线AB和直线CD:y=x+3的交点M的坐标.
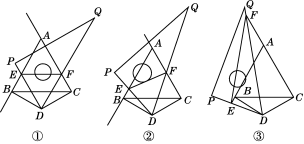
19.(5分)点D是等边三角形ABC外一点,且DB=DC,∠BDC=120°,将一个三角尺60°角的顶点放在点D上,三角尺的两边DP,DQ分别与射线AB,CA相交于E,F两点.
(1)当EF∥BC时,如图①所示,求证:EF=BE+CF.
(2)当三角尺绕点D旋转到如图②所示的位置时,线段EF,BE,CF之间的上述数量关系是否成立?如果成立,请说明理由;如果不成立,写出EF,BE,CF之间的数量关系,并说明理由.
(3)当三角尺绕点D继续旋转到如图③所示的位置时,(1)中的结论是否发生变化?如果不变化,直接写出结论;如果变化,请直接写出EF,BE,CF之间的数量关系.
20.(8分)如图,在▱ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连接BE、BF,使它们分别与AO相交于点G、H.
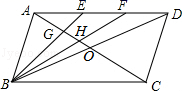
(1)求EG:BG的值;
(2)求证:AG=OG;
(3)设AG=a,GH=b,HO=c,求a:b:c的值.
21.(10分)涡阳某童装专卖店在销售中发现,一款童装每件进价为![]() 元,销售价为
元,销售价为![]() 元时,每天可售出
元时,每天可售出![]() 件,为了迎接“六-一”儿童节,商店决定采取适当的降价措施,以扩大销售增加利润,经市场调查发现,如果每件童装降价
件,为了迎接“六-一”儿童节,商店决定采取适当的降价措施,以扩大销售增加利润,经市场调查发现,如果每件童装降价![]() 元,那么平均可多售出
元,那么平均可多售出![]() 件.
件.
(1)若每件童装降价![]() 元,每天可售出 件,每件盈利 元(用含
元,每天可售出 件,每件盈利 元(用含![]() 的代数式表示);
的代数式表示);
![]() 每件童装降价多少元时,能让利于顾客并且商家平均每天能赢利
每件童装降价多少元时,能让利于顾客并且商家平均每天能赢利![]() 元.
元.
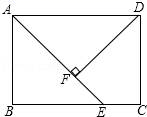
22.(10分)如图,在矩形ABCD,AD=AE,DF⊥AE于点F.求证:AB=DF.
23.(12分)若x、y都是实数,且y=![]() +
+![]() +
+![]() ,求x2y+xy2的值.
,求x2y+xy2的值.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、B
2、A
3、A
4、A
5、A
6、B
7、B
8、D
9、C
10、D
11、A
12、C
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、2![]() 或10.
或10.
14、(22008-1,22008)
15、1:1
16、![]()
17、1
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)y=3x+1;(2)M(1,4).
19、(1)见解析;(2)结论仍然成立.理由见解析;(3)结论发生变化.EF=CF-BE.
20、(1)1:3;(1)见解析;(3)5:3:1.
21、 (1)![]() ;(2)每件童装降价
;(2)每件童装降价![]() 元时,平均每天盈利
元时,平均每天盈利![]() 元.
元.
22、见解析
23、1![]() +1.
+1.
四川省南充市顺庆区2023-2024学年九上数学期末经典试题含答案: 这是一份四川省南充市顺庆区2023-2024学年九上数学期末经典试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,一元二次方程的根为,《孙子算经》中有一道题等内容,欢迎下载使用。
2023-2024学年四川省南充市顺庆区数学八上期末达标检测试题含答案: 这是一份2023-2024学年四川省南充市顺庆区数学八上期末达标检测试题含答案,共7页。试卷主要包含了答题时请按要求用笔,若分式的值为零,则x的值为等内容,欢迎下载使用。
四川省南充市阆中学2022-2023学年七年级数学第二学期期末复习检测模拟试题含答案: 这是一份四川省南充市阆中学2022-2023学年七年级数学第二学期期末复习检测模拟试题含答案,共6页。试卷主要包含了考生要认真填写考场号和座位序号,因式分解的正确结果是等内容,欢迎下载使用。













