2022-2023学年吉林省长春市净月高新区七下数学期末经典模拟试题含答案

2022-2023学年吉林省长春市净月高新区七下数学期末经典模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

考生须知：

1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。

2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。

3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、选择题(每小题3分,共30分)

1．当1＜a＜2时，代数式＋|1－a|的值是(     )

A．－1 B．1 C．2a－3 D．3－2a

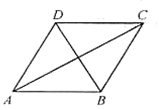
2．如图，已知某广场菱形花坛的周长是24米，，则此花坛的面积等于（    ）

A．平方米 B．24平方米 C．平方米 D．平方米

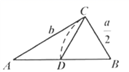
3．欧几里得的《原本》记载，形如的方程的图解法是：画，使，，，再在斜边上截取.则该方程的一个正根是（   ）

A．的长 B．的长 C．的长 D．的长

4．如图为某城市部分街道示意图，四边形ABCD为正方形，点G在对角线BD上，GE⊥CD，GF⊥BC，AD=1500m，小敏行走的路线为B→A→G→E，小聪行走的路线为B→A→D→E→F，若小敏行走的路程为3100m，则小聪行走的路程为（　　）m．

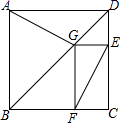
A．3100 B．4600 C．3000 D．3600

5．方程2x2﹣3x﹣5=0的二次项系数、一次项系数、常数项分别为（　　）

A．3、2、5    B．2、3、5    C．2、﹣3、﹣5    D．﹣2、3、5

6．如图，已知菱形ABCD的边长为2，∠DAB=60°，则对角线BD的长是（ ）

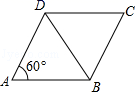
A．1 B． C．2 D．

7．设a= ，b= ，c=，则a，b，c的大小关系是（    ）

A．b>c>a                               B．b>a>c                               C．c＞a＞b                               D．a＞c＞b

8．如图，在△ABC 中， AB 的垂直平分线交 BC 于 D，AC 的中垂线交 BC 于 E，∠BAC=112°，则∠DAE 的度数为（　）

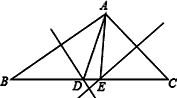
A．68° B．56° C．44° D．24°

9．下列分式中，是最简分式的是

A． B． C． D．

10．不等式组的正整数解的个数有（ ）

A．1个 B．2个 C．3个 D．4个

二、填空题(本大题共有6小题，每小题3分，共18分)

11．使为整数的的值可以是________（只需填一个）.

12．《九章算术》卷九“勾股”中记载：今有立木，系索其末，委地三尺．引索却行，去本八尺而索尽，问索长几何？译文：今有一竖立着的木柱，在木柱的上端系有绳索，绳索从木柱上端顺木柱下垂后，堆在地面的部分尚有3尺．牵着绳索（绳索头与地面接触）退行，在距木根部8尺处时绳索用尽．问绳索长是多少？设绳索长为x尺，可列方程为_____．

13．已知一组数据1,2,0,-1,x,1的平均数是1,则这组数据的极差为____.

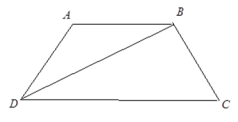
14．如图，在等腰梯形中，∥ ，，⊥，则∠=________．

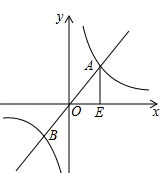
15．如图，已知函数y=2x和函数y=的图象交于A、B两点，过点A作AE⊥x轴于点E，若△AOE的面积为4，P是坐标平面上的点，且以点B、O、E、P为顶点的四边形是平行四边形，则k=_____，满足条件的P点坐标是_________________．

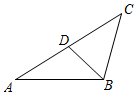
16．如图，已知△ABC∽△ADB，若AD＝2，CD＝2，则AB的长为_____．

三、解下列各题(本大题共8小题，共72分)

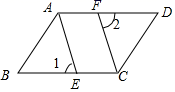
17．（8分）如图，在▱ABCD中，E、F分别是BC、AD边上的点，且∠1=∠1．求证：四边形AECF是平行四边形．

18．（8分）如图，在中，对角线AC，BD交于点O，E是AD上任意一点，连接EO并延长，交BC于点F，连接AF，CE.

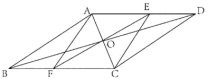
（1）求证：四边形AFCE是平行四边形；

（2）若，°，.

①直接写出的边BC上的高h的值；

②当点E从点D向点A运动的过程中，下面关于四边形AFCE的形状的变化的说法中，正确的是

A．平行四边形→矩形→平行四边形→菱形→平行四边形

B．平行四边形→矩形→平行四边形→正方形→平行四边形

C．平行四边形→菱形→平行四边形→菱形→平行四边形

D．平行四边形→菱形→平行四边形→矩形→平行四边形

19．（8分）如图，已知正方形ABCD的边长为6，点E、F分别在BC、DC上，CE=DF=2，DE与AF相交于点G，点H为AE的中点，连接GH．

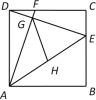
（1）求证：△ADF≌△DCE；

（2）求GH的长．

20．（8分）直线与轴、轴分别交于两点，以为边向外作正方形，对角线交于点，则过两点的直线的解析式是__________．

21．（8分）阅读材料：各类方程的解法

求解一元一次方程，根据等式的基本性质，把方程转化为x=a的形式．求解二元一次方程组，把它转化为一元一次方程来解；类似的，求解三元一次方程组，把它转化为解二元一次方程组．求解一元二次方程，把它转化为两个一元一次方程来解．求解分式方程，把它转化为整式方程来解，由于“去分母”可能产生增根，所以解分式方程必须检验．各类方程的解法不尽相同，但是它们有一个共同的基本数学思想转化，把未知转化为已知．

用“转化”的数学思想，我们还可以解一些新的方程．例如，一元三次方程x3+x2-2x=0，可以通过因式分解把它转化为x(x2+x-2)=0，解方程x=0和x2+x-2=0，可得方程x3+x2-2x=0的解．

（1）问题：方程x3+x2-2x=0的解是x1=0,x2=       ，x3=    ；

（2）拓展：用“转化”思想求方程的解；

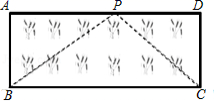
（3）应用：如图，已知矩形草坪ABCD的长AD=8m，宽AB=3m，小华把一根长为10m的绳子的一端固定在点B，沿草坪边沿BA，AD走到点P处，把长绳PB段拉直并固定在点P，然后沿草坪边沿PD、DC走到点C处，把长绳剩下的一段拉直，长绳的另一端恰好落在点C．求AP的长．

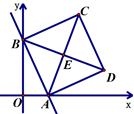
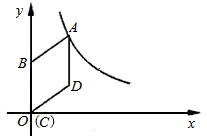
22．（10分）如图，在平面直角坐标系中，菱形的顶点与原点重合，点在轴的正半轴上，点在函数的图象上，点的坐标为.

(1)求的值.

(2)将点沿轴正方向平移得到点，当点在函数的图象上时，求的长.

23．（10分）某市团委举办“我的中国梦”为主题的知识竞赛，甲、乙两所学校参赛人数相等，比赛结束后，发现学生成绩分别为70分，80分，90分，100分，并根据统计数据绘制了如下不完整的统计图表：

乙校成绩统计表

（1）在图①中，“80分”所在扇形的圆心角度数为；

（2）请你将图②补充完整；

（3）求乙校成绩的平均分；

（4）经计算知S甲2=135，S乙2=175，请你根据这两个数据，对甲、乙两校成绩作出合理评价．

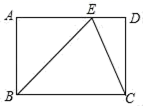
24．（12分）如图，在矩形ABCD中，点E在AD上，EC平分∠BED

（1）判断△BEC的形状，并加以证明；

（2）若∠ABE＝45°，AB＝2时，求BC的长．

参考答案

一、选择题(每小题3分,共30分)

1、B

2、C

3、B

4、B

5、C

6、C

7、B

8、C

9、D

10、C

二、填空题(本大题共有6小题，每小题3分，共18分)

11、1．

12、（x﹣3）2+64＝x2

13、4

14、60°

15、8    P1（0，-4），P2（-4，-4），P3（4，4）   

16、2．

三、解下列各题(本大题共8小题，共72分)

17、详见解析

18、（1）见解析；（2）①；②D

19、（1）详见解析；（2）

20、

21、 (1)-2，1；（2）x=3；（3）4m.

22、 (1)k＝12；(2)DD′=.

23、（1）54°；（2）见解析；（3）85；（4）甲班20同名同学的成绩比较整齐．

24、（1）详见解析；（2）