2022-2023学年吉林省大安市第三中学七下数学期末监测试题含答案

2022-2023学年吉林省大安市第三中学七下数学期末监测试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验，它们的平均亩产量分别是=610千克，=608千克，亩产量的方差分别是="29." 6，="2." 7. 则关于两种小麦推广种植的合理决策是 （ ）

A．甲的平均亩产量较高，应推广甲

B．甲、乙的平均亩产量相差不多，均可推广

C．甲的平均亩产量较高，且亩产量比较稳定，应推广甲

D．甲、乙的平均亩产量相差不多，但乙的亩产量比较稳定，应推广乙

2．如图，正方形ABCD的边长为8，点M在DC上，且DM=2，N是AC上一动点，则DN+MN的最小值为（）

A．8 B． C． D．10

3．如图，在△ABC中，点D，E分别是边AB，AC的中点，已知DE＝3，则BC的长为（　　）

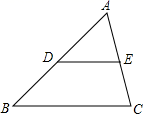
A．3 B．4 C．6 D．5

4．下表记录了甲、乙、丙、丁四名同学最近几次数学考试成绩的平均数与方差：

要选择一名成绩好且发挥稳定的同学参加数学比赛，应该选择（　　）

A．甲 B．乙 C．丙 D．丁

5．下列调查中，不适合普查但适合抽样调查的是（   ）

A．调查年级一班男女学生比例 B．检查某书稿中的错别字

C．调查夏季冷饮市场上冰淇凌的质量 D．调查载人航天飞船零件部分的质量

6．有11名同学参加100米赛跑，预赛成绩各不相同，要取前6名参加决赛，小明已经知道了自己的成绩，他想知道自己能否进入决赛，还需要知道这11名同学成绩的（    ）

A．中位数 B．平均数 C．众数 D．方差

7．估计的结果在（   ）.

A．8至9之间 B．9至10之间 C．10至11之间 D．11至12之间

8．方程的根是　　

A． B． C．， D．，

9．如图，在正方形ABCD中，点F为CD上一点，BF与AC交于点E．若∠CBF＝20°，则∠DEF的度数是(   )

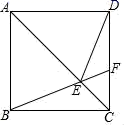
A．25° B．40° C．45° D．50°

10．一个正比例函数的图象经过点，则它的解析式为（　　）

A． B． C． D．

11．如图，在平行四边形中，对角线交于点，并且，点是边上一动点，延长交于点，当点从点向点移动过程中（点与点，不重合），则四边形的变化是（    ）

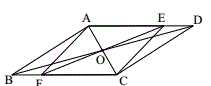
A．平行四边形→菱形→平行四边形→矩形→平行四边形

B．平行四边形→矩形→平行四边形→菱形→平行四边形

C．平行四边形→矩形→平行四边形→正方形→平行四边形

D．平行四边形→矩形→菱形→正方形→平行四边形

12．若关于x的分式方程无解，则m的值为（ ）

A．一l.5 B．1 C．一l.5或2 D．一0.5或一l.5

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．使有意义的x的取值范围是_____．

14．若点在轴上，则点的坐标为__________．

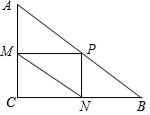
15．如图，在R△ABC中，∠C＝90°，AC＝3，BC＝4，点P是AB上的一个动点，过点P作PM⊥AC于点M，PN⊥BC于点N，连接MN，则MN的最小值为_____．

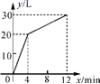
16．一个有进水管和出水管的容器，从某时刻开始4 min内只进水不出水，在随后的8 min内既进水又出水，每分钟的进水量和出水量是两个常数，容器内的水量y(L)与时间x(min)之间的关系如图所示，则每分钟的出水量为________________

17．已知点M（-1，），N（，-2）关于x轴对称，则=_____

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）如图，等腰△ABC中，已知AC＝BC＝2， AB＝4，作∠ACB的外角平分线CF，点E从点B沿着射线BA以每秒2个单位的速度运动，过点E作BC的平行线交CF于点F．

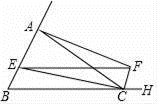
（1）求证：四边形BCFE是平行四边形；   

（2）当点E是边AB的中点时，连接AF，试判断四边形AECF的形状，并说明理由；   

（3）设运动时间为t秒，是否存在t的值，使得以△EFC的其中两边为邻边所构造的平行四边形恰好是菱形？不存在的，试说明理由；存在的，请直接写出t的值．答：t＝________．

19．（5分）如图，在菱形中，.请根据下列条件，仅用无刻度的直尺过顶点作菱形的边上的高。

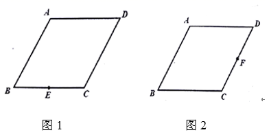
（1）在图1中，点为中点；

（2）在图2中，点为中点.

20．（8分）如图，4×6的正方形网格中，每个小正方形的顶点称为格点，A，B，C均为格点.在下列各图中画出四边形ABCD，使点D也为格点，且四边形ABCD分别符合下列条件: 

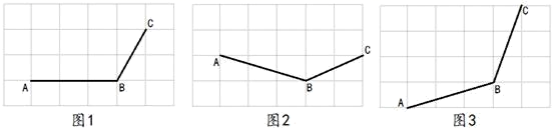
（1）是中心对称图形(画在图1中)   

（2）是轴对称图形(画在图2中)   

（3）既是轴对称图形，又是中心对称图形(画在图3中)

21．（10分）解不等式组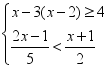：，并将解集在数轴上表示出来．

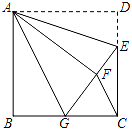
22．（10分）如图，正方形ABCD中，CD=6，点E在边CD上，且CD=3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．

（1）求证：△ABG≌△AFG；

（2）求GC的长．

23．（12分）如图，在四边形中，，，对角线，交于点，平分，过点作交的延长线于点，连接．

（1）求证：四边形是菱形；

（2）若，，求的长．

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、D

2、D

3、C

4、B

5、C

6、A

7、C

8、C

9、D

10、C

11、A

12、D

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、x≥2

14、

15、2.1

16、L

17、1

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1）见解析；（2）四边形AECF是矩形，理由见解析；（3）秒或5秒或2秒

19、（1）见解析；（2）见解析.

20、（1）详见解析；（2）详见解析；（3）详见解析；

21、-7＜≤1.数轴见解析.

22、（1）证明见解析；（2）3.

23、（1）证明见解析；（2）2.