


2022-2023学年北京市高级中学等学校数学七年级第二学期期末学业质量监测试题含答案
展开2022-2023学年北京市高级中学等学校数学七年级第二学期期末学业质量监测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.函数y=ax﹣a与y=![]() (a≠0)在同一直角坐标系中的图象可能是( )
(a≠0)在同一直角坐标系中的图象可能是( )
A.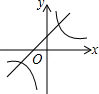 B.
B.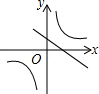
C.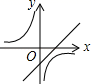 D.
D.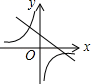
2.等腰三角形的两条边长分别为3和4,则其周长等于( )
A.10 B.11 C.10或11 D.不确定
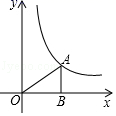
3.如图,点A在函数y=![]() (x>0)的图象上,且OA=4,过点A作AB⊥x轴于点B,则△ABO的周长为( )
(x>0)的图象上,且OA=4,过点A作AB⊥x轴于点B,则△ABO的周长为( )
A.2![]() B.2
B.2![]() C.2
C.2![]() +4 D.2
+4 D.2![]() +4
+4
4.下列不等式的变形中,不正确的是( )
A.若![]() ,则
,则![]() B.若
B.若![]() ,则
,则![]()
C.若![]() ,则
,则![]() D.若
D.若![]() ,则
,则![]()
5.从![]() ,0,π,3.14,6这5个数中随机抽取一个数,抽到有理数的概率是( )
,0,π,3.14,6这5个数中随机抽取一个数,抽到有理数的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知多项式![]() 是一个关于
是一个关于![]() 的完全平方式,则
的完全平方式,则![]() 的值为( )
的值为( )
A.3 B.6 C.3或-3 D.6或-6
7.下列各式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中分式有( )
,其中分式有( )
A.2个 B.3个 C.4个 D.5个
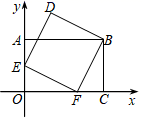
8.如图,在平面直角坐标系xOy中,点A、C、F在坐标轴上,E是OA的中点,四边形AOCB是矩形,四边形BDEF是正方形,若点C的坐标为(3,0),则点D的坐标为( )
A.(1,2.5) B.(1,1+ ![]() ) C.(1,3) D.(
) C.(1,3) D.(![]() ﹣1,1+
﹣1,1+ ![]() )
)
9.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,则
,则![]() 的周长为( )
的周长为( )
A.12 B.14 C.15 D.20
10.漳州市政府为了鼓励市民绿色出行,投资了一批城市公共自行车,收费如下:第1小时内免费,1小时以上,每半小时收费0.5元(不到半小时按半小时计).马小跳刷卡时显示收费1.5元,则马小跳租车时间x的取值范围为( )
A.1<x≤1.5 B.2<x≤2.5 C.2.5<x≤3 D.3<x≤4
11.若不等式组![]() 的解集为
的解集为![]() ,则
,则![]() 的值等于( )
的值等于( )
A.![]() B.
B.![]() C.2 D.4
C.2 D.4
12.下列调查中,最适合采用全面调查(普查)方式的是( )
A.对重庆市初中学生每天阅读时间的调查
B.对端午节期间市场上粽子质量情况的调查
C.对某批次手机的防水功能的调查
D.对某校九年级3班学生肺活量情况的调查
二、填空题(每题4分,满分20分,将答案填在答题纸上)
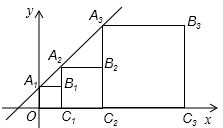
13.正方形A1B1C1O,正方形A2B2C2C1,正方形A3B3C3C2,按如图所示的方式放置在平面直角坐标系中,若点A1、A2、A3和C1、C2、C3…分别在直线y=x+1和x轴上,则点B2019的坐标是_____.
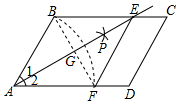
14.如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() BF的相同长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为16,∠C=60°,则四边形ABEF的面积是___.
BF的相同长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为16,∠C=60°,则四边形ABEF的面积是___.
15.在▱ABCD中,AD=BD,BE是AD边上的高,∠EBD=20°,则∠A的度数为 .
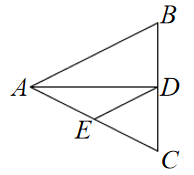
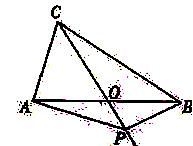
16.如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为 .
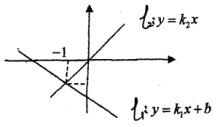
17.直线![]() 与直线
与直线![]() 在同一平面直角坐标系中如图所示,则关于x的不等式
在同一平面直角坐标系中如图所示,则关于x的不等式![]() 的解为________________.
的解为________________.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)在平面直角坐标系中,已知点![]() ,
,![]() ,
,![]() ,点
,点![]() 与
与![]() 关于
关于![]() 轴对称.
轴对称.
(1)写出点![]() 所在直线的函数解析式;
所在直线的函数解析式;
(2)连接![]() ,若线段
,若线段![]() 能构成三角形,求
能构成三角形,求![]() 的取值范围;
的取值范围;
(3)若直线![]() 把四边形
把四边形![]() 的面积分成相等的两部分,试求
的面积分成相等的两部分,试求![]() 的值.
的值.
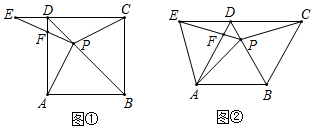
19.(5分)如图![]() ,在正方形ABCD中,P是对角线BD上的一点,点E在CD的延长线上,且
,在正方形ABCD中,P是对角线BD上的一点,点E在CD的延长线上,且![]() ,PE交AD于点F.
,PE交AD于点F.
![]() 求证:
求证:![]() ;
;
![]() 求
求![]() 的度数;
的度数;
![]() 如图
如图![]() ,把正方形ABCD改为菱形ABCD,其它条件不变,当
,把正方形ABCD改为菱形ABCD,其它条件不变,当![]() ,连接AE,试探究线段AE与线段PC的数量关系,并给予证明.
,连接AE,试探究线段AE与线段PC的数量关系,并给予证明.
20.(8分)在四边形ABCD中,E、F分别是边BC、CD的中点,连接AE,AF.
(1)如图1,若四边形ABCD的面积为5,则四边形AECF的面积为____________;
(2)如图2,延长AE至G,使EG=AE,延长AF至H,使FH=AF,连接BG、GH、HD、DB.
求证:四边形BGHD是平行四边形;
(3)如图3,对角线 AC、BD相交于点M, AE与BD交于点P, AF与BD交于点N. 直接写出BP、PM、MN、ND的数量关系.

21.(10分)如图,已知火车站的坐标为(2,2),文化宫的坐标为(-1,3).
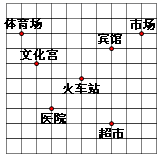
(1)请你根据题目条件,画出平面直角坐标系;
(2)写出体育场,市场,超市的坐标;
(3)已知游乐场A,图书馆B,公园C的坐标分别为(0,5),(-2,-2),(2,-2),请在图中标出A,B,C的位置.
22.(10分)甲、乙两列火车分别从A、B两城同时匀速驶出,甲车开往B城,乙车开往A城.由于墨迹遮盖,图中提供的是两车距B城的路程S甲(千米)、S乙(千米)与行驶时间t(时)的函数图象的一部分.

(1)分别求出S甲、S乙与t的函数关系式(不必写出t的取值范围);
(2)求A、B两城之间的距离,及t为何值时两车相遇;
(3)当两车相距300千米时,求t的值.
23.(12分)某校美术社团为练习素描,他们第一次用120元买了若干本资料,第二次又用240元在同一商家买同样的资料,这次商家每本优惠4元,结果比上次多买了20本.求第一次买了多少本资料?
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、D
2、C
3、D
4、D
5、C
6、D
7、B.
8、C
9、B
10、B
11、B
12、D
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]() .
.
14、8![]() .
.
15、55°或35°.
16、1或1![]() 或1
或1![]()
17、![]() ;
;
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)![]() ;(2)
;(2)![]() 时,线段
时,线段![]() 能构成三角形;(3)当
能构成三角形;(3)当![]() 时,
时,![]() 把四边形
把四边形![]() 的面积分成相等的两部分.
的面积分成相等的两部分.
19、![]() 证明见解析
证明见解析![]() 证明见解析
证明见解析![]() ,
,
20、(1)![]() (2)证明见解析(3)
(2)证明见解析(3)![]() .
.
21、(1)图形见解析(2)体育场(-2,5)市场(6,5)超市(4,-1)(3)图形见解析
22、(1)S甲=-180t+600,S乙=120t;(2)A、B两城之间的距离是600千米,t为2时两车相遇;(1)当两车相距100千米时,t的值是1或1.
23、第一次买了11本资料.
北京市北京昌平临川育人学校2023-2024学年八上数学期末学业质量监测模拟试题含答案: 这是一份北京市北京昌平临川育人学校2023-2024学年八上数学期末学业质量监测模拟试题含答案,共8页。试卷主要包含了考生要认真填写考场号和座位序号,9的平方根是,点P关于y轴对称的点的坐标是,有下列五个命题,下列说法正确的是,是一个完全平方式,则k等于,计算的结果是等内容,欢迎下载使用。
北京市怀柔区2022-2023学年数学七年级第二学期期末学业质量监测试题含答案: 这是一份北京市怀柔区2022-2023学年数学七年级第二学期期末学业质量监测试题含答案,共8页。试卷主要包含了考生要认真填写考场号和座位序号等内容,欢迎下载使用。
北京市部分区2022-2023学年七下数学期末学业质量监测模拟试题含答案: 这是一份北京市部分区2022-2023学年七下数学期末学业质量监测模拟试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,下列计算错误的是等内容,欢迎下载使用。













