


2022-2023学年北京市丰台区数学七下期末统考模拟试题含答案
展开2022-2023学年北京市丰台区数学七下期末统考模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.
一、选择题(每小题3分,共30分)
1.某校九年级体育模拟测试中,六名男生引体向上的成绩如下(单位:个):
10,6,9,11,8,10. 下列关于这组数据描述正确的是 ( )
A.中位数是10 B.众数是10 C.平均数是9.5 D.方差是16
2.如图,若要使▱ABCD成为矩形,需添加的条件是( )
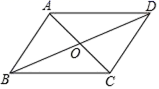
A.AB=BC B.∠ABD=∠DBC C.AO=BO D.AC⊥BD
3.如图,用一根绳子检查一个书架的侧边是否和上、下底都垂直,只需要用绳子分别测量比较书架的两条对角线![]() 就可以判断,其数学依据是( )
就可以判断,其数学依据是( )
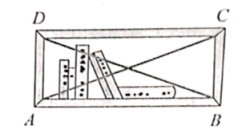
A.三个角都是直角的四边形是矩形
B.对角线互相平分的四边形是平行四边形
C.对角线相等的平行四边形是矩形
D.对角线互相垂直平分的四边形是菱形
4.已知等腰△ABC的两边长分别为2和3,则等腰△ABC的周长为( )
A.7 B.8 C.6或8 D.7或8
5.如图,![]() 、
、![]() 两点在反比例函数
两点在反比例函数![]() 的图象上,
的图象上,![]() 、
、![]() 两点在反比例函数
两点在反比例函数![]() 的图象上,
的图象上,![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 的值是( )
的值是( )
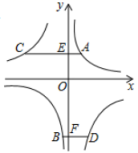
A.8 B.6 C.4 D.10
6.如图,正方形ABCD的边长为3,E在BC上,且BE=2,P在BD上,则PE+PC的最小值为( )
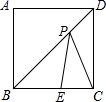
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.下列电视台的台标,是中心对称图形的是( )
A. B.
B. C.
C. D.
D.
8.如果点![]() 在正比例函数
在正比例函数![]() 的图像上,那么下列等式一定成立的是( )
的图像上,那么下列等式一定成立的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
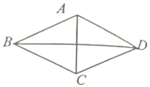
9.如图,菱形![]() 中,
中,![]() ,这个菱形的周长是( )
,这个菱形的周长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.如图,∠1,∠2,∠3,∠4,∠5是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=75°,则∠AED的度数是( )

A.120° B.110° C.115° D.100°
二、填空题(本大题共有6小题,每小题3分,共18分)
11.一个平行四边形的一条边长为3,两条对角线的长分别为4和![]() ,则它的面积为______.
,则它的面积为______.
12.因式分解:x2﹣9y2= .
13.点M(a,﹣5)与点N(﹣2,b)关于x轴对称,则a+b=________.
14.甲、乙两人进行射击测试,每人10次射击成绩的平均数都是8.5环,方差分别是:S甲2=2,S乙2=1.5,则射击成绩较稳定的是 (填“甲”或“乙“).
15.一组数据2,3,4,5,3的众数为__________.
16.某车间6名工人日加工零件数分别为6,10,8,10,5,8,则这组数据的中位数是_____________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)定义:点![]() 关于原点的对称点为
关于原点的对称点为![]() ,以
,以![]() 为边作等边
为边作等边![]() ,则称点
,则称点![]() 为
为![]() 的“等边对称点”;
的“等边对称点”;
(1)若![]() ,求点
,求点![]() 的“等边对称点”的坐标;
的“等边对称点”的坐标;
(2)若![]() 点是双曲线
点是双曲线![]() 上动点,当点
上动点,当点![]() 的“等边对称点”点
的“等边对称点”点![]() 在第四象限时,
在第四象限时,
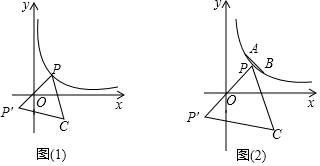
①如图(1),请问点![]() 是否也会在某一函数图象上运动?如果是,请求出此函数的解析式;如果不是,请说明理由;
是否也会在某一函数图象上运动?如果是,请求出此函数的解析式;如果不是,请说明理由;
②如图(2),已知点![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上的动点,点
上的动点,点![]() 在
在![]() 轴上,若以
轴上,若以![]() 、
、![]() 、
、![]() 、
、![]() 这四个点为顶点的四边形是平行四边形时,求点
这四个点为顶点的四边形是平行四边形时,求点![]() 的纵坐标
的纵坐标![]() 的取值范围.
的取值范围.
18.(8分)2008年6月1日起,我国实施“限塑令”,开始有偿使用环保购物袋.为了满足市场需求,某厂家生产![]() 两种款式的布质环保购物袋,每天共生产4500个,两种购物袋的成本和售价如下表,设每天生产
两种款式的布质环保购物袋,每天共生产4500个,两种购物袋的成本和售价如下表,设每天生产![]() 种购物袋
种购物袋![]() 个,每天共获利
个,每天共获利![]() 元.
元.
| 成本(元/个) | 售价(元/个) |
| 2 | 2.3 |
| 3 | 3.5 |
(1)求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)如果该厂每天最多投入成本10000元,那么每天最多获利多少元?
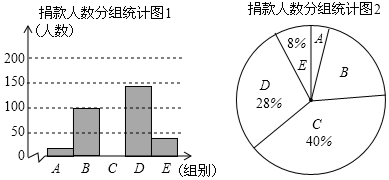
19.(8分)昆明市某校学生会干部对校学生会倡导的“牵手滇西”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).已知A、B两组捐款人数的比为1:1.
组别 | 捐款额x/元 | 人数 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 |
|
D | 30≤x<40 |
|
E | 40≤x<10 |
|
请结合以上信息解答下列问题.
(1)a= ,本次调查样本的容量是 ;
(2)先求出C组的人数,再补全“捐款人数分组统计图1”;
(3)根据统计情况,估计该校参加捐款的4100名学生有多少人捐款在20至40元之间.
20.(8分)甲乙两位同学参加数学综合素质测试,各项成绩如下表:(单位:分)
| 数与代数 | 空间与图形 | 统计与概率 | 综合与实践 |
学生甲 | 93 | 93 | 89 | 90 |
学生乙 | 94 | 92 | 94 | 86 |
(1)分别计算甲、乙同学成绩的中位数;
(2)如果数与代数,空间与图形,统计与概率,综合与实践的成绩按4:3:1:2计算,那么甲、乙同学的数学综合素质成绩分别为多少分?
21.(8分)计算
(1)![]() ×
×![]()
(2)(![]() )0+
)0+![]() -(-
-(-![]() )-2
)-2
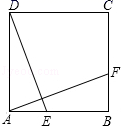
22.(10分)如图,正方形ABCD中,E、F分别是AB、BC边上的点,且AE=BF,求证:AF⊥DE.
23.(10分)如图,在▱ABCD中,AC、BD交于点O,BD⊥AD于点D,将△ABD沿BD翻折得到△EBD,连接EC、EB.
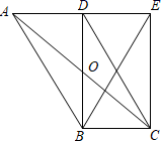
(1)求证:四边形DBCE是矩形;
(2)若BD=4,AD=3,求点O到AB的距离.
24.(12分)为提高市民的精神生活美化城市环境,城市管理局从外地新进一批绿化树苗,现有两种运输方式可供选择,
方式一:使用快递公司的邮车运输,装卸收费500元,另外每公里再加收5元;
方式二:使用铁路运输公司的火车运输,装卸收费900元,另外每公里再加收3元.
(1)请分别写出邮车、火车运输的总费用为![]() (元)、
(元)、![]() (元)与运输路程
(元)与运输路程![]() (公里)之间的函数关系式;
(公里)之间的函数关系式;
(2)你认为选用哪种运输方式较好,为什么?
参考答案
一、选择题(每小题3分,共30分)
1、B
2、C
3、C
4、D
5、A
6、B
7、D
8、D
9、C
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、4![]()
12、![]() .
.
13、2
14、乙
15、1.
16、1.
三、解下列各题(本大题共8小题,共72分)
17、(1)![]() 或
或![]() ;(2)①
;(2)①![]() ;②
;②![]() 或
或![]()
18、(1)![]() ;(2)1.
;(2)1.
19、 (1)20,100;(2)见解析;(3)3060人
20、(1)甲的中位数91.5,乙的中位数93;(2)甲的数学综合成绩92,乙的数学综合成绩91.1.
21、(1)![]() ;(2)2
;(2)2![]() -1
-1
22、证明见解析
23、(1)见解析;(2)点O到AB的距离为![]() .
.
24、(1)![]() ,
,![]() ;(2)当运输路程等于200千米时,
;(2)当运输路程等于200千米时,![]() ,用两种运输方式一样;当运输路程小于200千米时,
,用两种运输方式一样;当运输路程小于200千米时,![]() ,用邮车运输较好;当运输路程大于200千米时,
,用邮车运输较好;当运输路程大于200千米时,![]() ,用火车运输较好.
,用火车运输较好.
北京市西城区2022-2023学年七下数学期末统考模拟试题含答案: 这是一份北京市西城区2022-2023学年七下数学期末统考模拟试题含答案,共7页。试卷主要包含了一组数,分式的计算结果是,若分式的值为0,则,在中,若是的正比例函数,则值为等内容,欢迎下载使用。
北京市海淀区名校2022-2023学年数学七下期末统考模拟试题含答案: 这是一份北京市海淀区名校2022-2023学年数学七下期末统考模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,下列判断中,错误的是,函数与等内容,欢迎下载使用。
北京市昌平区新道临川学校2022-2023学年七下数学期末统考模拟试题含答案: 这是一份北京市昌平区新道临川学校2022-2023学年七下数学期末统考模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,点A等内容,欢迎下载使用。













