2022-2023学年北京大兴北臧村中学七年级数学第二学期期末考试试题含答案

2022-2023学年北京大兴北臧村中学七年级数学第二学期期末考试试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．直角三角形的两条直角边长分别为a和b，斜边长为c，已知c＝13，b＝5，则a＝（　　）

A．1 B．5 C．12 D．25

2．以下说法正确的是(    )

A．在367人中至少有两个人的生日相同；

B．一次摸奖活动的中奖率是l%，那么摸100次奖必然会中一次奖；

C．一副扑克牌中，随意抽取一张是红桃K，这是必然事件；

D．一个不透明的袋中装有3个红球，5个白球，任意摸出一个球是红球的概率是

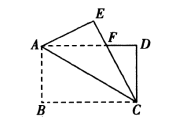
3．如图，矩形纸片中，，将沿折叠，使点落在点处，交于点，则的长等于(    )

A． B． C． D．

4．一元二次方程的根是（        ）

A． B． C．， D．无实数根

5．已知,,且,若,，则的长为（   ）

A．4 B．9 C． D．

6．下列数字中，不是不等式的解的是（  ）

A． B．0 C． D．4

7．若一个三角形三个内角度数的比为，且最大的边长为，那么最小的边长为（    ）

A．1 B． C．2 D．

8．有位同学参加歌咏比赛，所得的分数互不相同，取得分前位同学进入决赛，小明知道自己的分数后，要判断自己能否进入决赛，他只需知道这位同学得分的（    ）

A．平均数 B．中位数 C．众数 D．方差

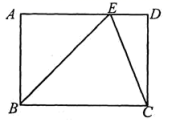
9．如图，在矩形ABCD中，点E在AD上，且EC平分∠BED，AB=1，∠ABE=45°，则BC的长为（    ）

A． B．1．5 C． D．2

10．下列实数中，是方程的根的是（     ）

A．1 B．2 C．3 D．4

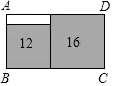
11．如图，在矩形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片，则图中空白部分的面积为(    )cm2.

A．16- B．-12+ C．8- D．4-

12．在数学活动课上，老师要求同学们判断一个四边形门框是否为矩形，下面是某合作学习小组的四位同学拟定的方案，其中正确的是（    ）

A．测量对角线是否相互平分 B．测量两组对边是否分别相等

C．测量一组对角是否都为直角 D．测量四边形其中的三个角是否都为直角

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．如果一组数据：5，，9，4的平均数为6，那么的值是_________

14．已知等腰三角形两条边的长为4和9，则它的周长______.

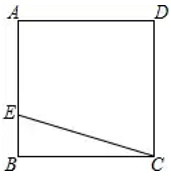
15．如图，四边形是一块正方形场地，小华和小芳在边上取定一点，测量知，，这块场地的对角线长是________．

16．一名主持人站在舞台的黄金分割点处最自然得体，如果舞台AB长为20m，这名主持人现在站在A处（如图所示），则它应至少再走_____m才最理想．(可保留根号).

17．某车间6名工人日加工零件数分别为6，10，8，10，5，8，则这组数据的中位数是_____________．

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）阅读材料：各类方程的解法

求解一元一次方程，根据等式的基本性质，把方程转化为x=a的形式．求解二元一次方程组，把它转化为一元一次方程来解；类似的，求解三元一次方程组，把它转化为解二元一次方程组．求解一元二次方程，把它转化为两个一元一次方程来解．求解分式方程，把它转化为整式方程来解，由于“去分母”可能产生增根，所以解分式方程必须检验．各类方程的解法不尽相同，但是它们有一个共同的基本数学思想转化，把未知转化为已知．

用“转化”的数学思想，我们还可以解一些新的方程．例如，一元三次方程x3+x2-2x=0，可以通过因式分解把它转化为x(x2+x-2)=0，解方程x=0和x2+x-2=0，可得方程x3+x2-2x=0的解．

（1）问题：方程x3+x2-2x=0的解是x1=0,x2=       ，x3=    ；

（2）拓展：用“转化”思想求方程的解；

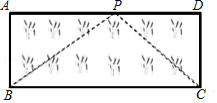
（3）应用：如图，已知矩形草坪ABCD的长AD=8m，宽AB=3m，小华把一根长为10m的绳子的一端固定在点B，沿草坪边沿BA，AD走到点P处，把长绳PB段拉直并固定在点P，然后沿草坪边沿PD、DC走到点C处，把长绳剩下的一段拉直，长绳的另一端恰好落在点C．求AP的长．

19．（5分）某文具店准备购进A、B两种型号的书包共50个进行销售，两种书包的进价、售价如下表所示：

购进这50个书包的总费用不超过7300元，且购进B型书包的个数不大于A型书包个数的．

（1）该文具店有哪几种进货方案？

（2）若该文具店购进的50个书包全部售完，则该文具店采用哪种进货方案，才能获得最大利润？最大利润是多少？（利润＝售价﹣进价）

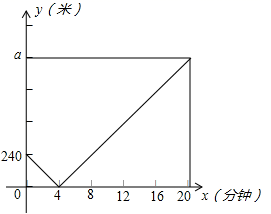
20．（8分）周末，小明、小刚两人同时各自从家沿直线匀速步行到科技馆参加科技创新活动，小明家、小刚家、科技馆在一条直线上．已知小明到达科技馆花了20分钟．设两人出发（分钟）后，小明离小刚家的距离为（米），与的函数关系如图所示．

（1）小明的速度为        米/分，       ，小明家离科技馆的距离为     米；

（2）已知小刚的步行速度是40米/分，设小刚步行时与家的距离为（米），请求出与之间的函数关系式，并在图中画出 （米）与 （分钟）之间的函数关系图象；

（3）小刚出发几分钟后两人在途中相遇？

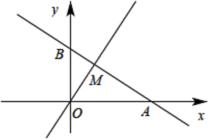
21．（10分）如图，直线与轴，轴分别交于点，点，与函数的图象交于点．

（1）直接写出k，b的值和不等式的解集；

（2）在轴上有一点，过点作轴的垂线，分别交函数和的图象于点，点．若，求点的坐标．

22．（10分）宝安区某街道对长为20千米的路段进行排水管道改造后，需对该段路面全部重新进行修整，甲、乙两个工程队将参与施工，已知甲队每天的工作效率是乙队的2倍，若由甲、乙两队分别单独修整长为800米的路面，甲队比乙队少用5天．

（1）求甲队每天可以修整路面多少米？

（2）若街道每天需支付给甲队的施工费用为0.4万元，乙队为0.25万元，如果本次路面修整预算55万元，为了不超出预算，至少应该安排甲队参与工程多少天？

23．（12分）如图，在边长为1个单位长度的小正方形组成的两个中，点都是格点．

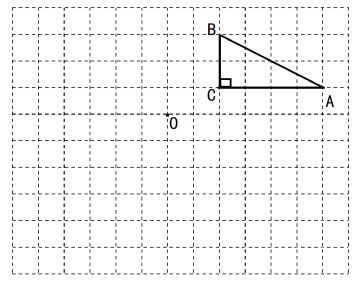
（1）将向左平移6个单位长度得到．请画出；

（2）将绕点按逆时针方向旋转得到，请画出．

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、C

2、A

3、B

4、C

5、B

6、A

7、B

8、B

9、A

10、B

11、B

12、D

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、6

14、1

15、40m

16、（30﹣10）

17、1．

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、 (1)-2，1；（2）x=3；（3）4m.

19、（1）有4种进货方案，分别是：①A，20个，B，30个；②A，21个，B，29个；③A，22个，B28个；④A，1个，B27个；（2）购进A型1个，B型27个获利最大，最大利润为3元．

20、（1）60；960；1200；（2）＝40（0≤≤24）；见解析；（3）12分钟．

21、（1）不等式的解集为；（2）点的坐标为 ，或，．

22、（1）1米；（2）2天

23、（1）图见详解；（1）图见详解．