2022-2023学年上海市廊下中学数学七年级第二学期期末经典试题含答案

2022-2023学年上海市廊下中学数学七年级第二学期期末经典试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项:

1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

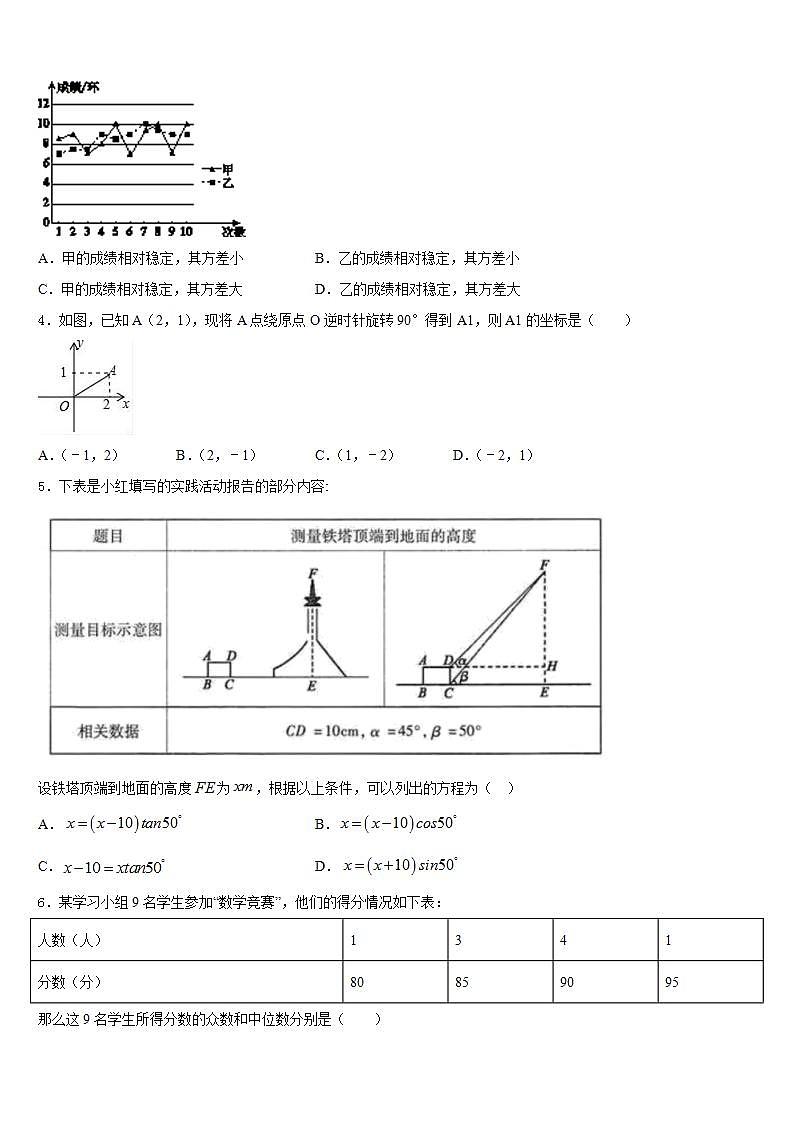
1．随着“中国诗词大会”节目的热播，《唐诗宋词精选》一书也随之热销．如果一次性购买10本以上，超过10本的那部分书的价格将打折，并依此得到付款金额y（单位：元）与一次性购买该书的数量x（单位：本）之间的函数关系如图所示，则下列结论错误的是（　　）

A．一次性购买数量不超过10本时，销售价格为20元/本

B．a＝520

C．一次性购买10本以上时，超过10本的那部分书的价格打八折

D．一次性购买20本比分两次购买且每次购买10本少花80元

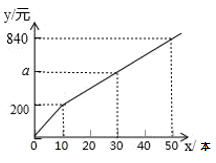
2．如图，已知四边形ABCD是平行四边形，下列结论中错误的是（　　）

A．当AB=BC时，它是菱形 B．当AC⊥BD时，它是菱形

C．当AC=BD时，它是矩形 D．当∠ABC=90°时，它是正方形

3．甲、乙两位射击运动员的10次射击练习成绩的折线统计图如图所示，则下列关于甲、乙这10次射击成绩的说法中正确的是（    ）

A．甲的成绩相对稳定，其方差小 B．乙的成绩相对稳定，其方差小

C．甲的成绩相对稳定，其方差大 D．乙的成绩相对稳定，其方差大

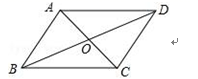
4．如图，已知A（2，1），现将A点绕原点O逆时针旋转90°得到A1，则A1的坐标是（　　）

A．（﹣1，2） B．（2，﹣1） C．（1，﹣2） D．（﹣2，1）

5．下表是小红填写的实践活动报告的部分内容:

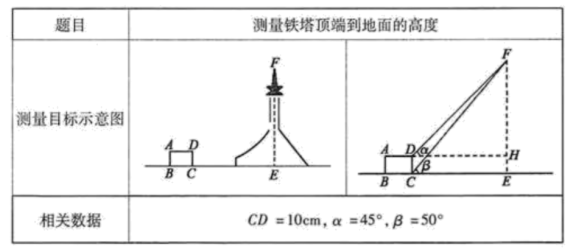
设铁塔顶端到地面的高度为，根据以上条件，可以列出的方程为（  ）

A． B．

C． D．

6．某学习小组9名学生参加“数学竞赛”，他们的得分情况如下表：

那么这9名学生所得分数的众数和中位数分别是（    ）

A．90，87.5 B．90，85 C．90，90 D．85，85

7．下列命题中，有几个真命题 (　      　)

①同位角相等   ②直角三角形的两个锐角互余

③平行四边形的对角线互相平分且相等     ④对顶角相等

A．1个 B．2个 C．3个 D．4个

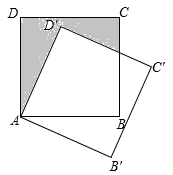
8．如图，边长为1的正方形ABCD绕点A顺时针旋转30°到AB′C′D′的位置，则图中阴影部分的面积为(　　)

A． B． C． D．

9．有位同学参加歌咏比赛，所得的分数互不相同，取得分前位同学进入决赛，小明知道自己的分数后，要判断自己能否进入决赛，他只需知道这位同学得分的（    ）

A．平均数 B．中位数 C．众数 D．方差

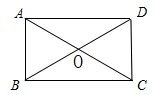
10．如图，在矩形ABCD中，AB=2，∠AOD=120°，则对角线AC等于（　　）

A．3 B．4 C．5 D．6

11．已知、是一次函数图象上的两个点，则与的大小关系为(   )

A． B． C． D．不能确定与的大小

12．一元二次方程x2-9=0的解为（    ）

A．x1=x2=3 B．x1=x2=-3 C．x1=3，x2=-3 D．x1=，x2=-

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．已知命题：全等三角形的对应角相等.这个命题的逆命题是：__________．

14．正六边形的每个内角等于______________°．

15．反比例函数的图象过点P（2，6），那么k的值是       ．

16．已知反比例函数的图像经过点、，则k的值等于_____.

17．用科学记数法表示______．

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）（2005•荆门）某校初中三年级270名师生计划集体外出一日游，乘车往返，经与客运公司联系，他们有座位数不同的中巴车和大客车两种车型可供选择，每辆大客车比中巴车多15个座位，学校根据中巴车和大客车的座位数计算后得知，如果租用中巴车若干辆，师生刚好坐满全部座位；如果租用大客车，不仅少用一辆，而且师生坐完后还多30个座位．

（1）求中巴车和大客车各有多少个座位？

（2）客运公司为学校这次活动提供的报价是：租用中巴车每辆往返费用350元，租用大客车每辆往返费用400元，学校在研究租车方案时发现，同时租用两种车，其中大客车比中巴车多租一辆，所需租车费比单独租用一种车型都要便宜，按这种方案需要中巴车和大客车各多少辆？租车费比单独租用中巴车或大客车各少多少元？

19．（5分）如图，在中，，、分别是、的中点，连接，过作交的延长线于．

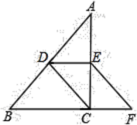
（1）证明：四边形是平行四边形；

（2）若四边形的周长是，的长为，求线段的长度．

20．（8分）等腰直角三角形OAB中，∠OAB＝90°，OA＝AB，点D为OA中点，DC⊥OB，垂足为C，连接BD，点M为线段BD中点，连接AM、CM，如图①．

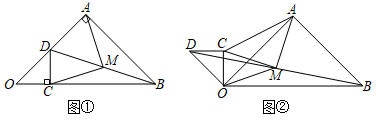
（1）求证：AM＝CM；

（2）将图①中的△OCD绕点O逆时针旋转90°，连接BD，点M为线段BD中点，连接AM、CM、OM，如图②．

①求证：AM＝CM，AM⊥CM；

②若AB＝4，求△AOM的面积．

21．（10分）已知二次函数的最大值为4，且该抛物线与轴的交点为，顶点为.

（1）求该二次函数的解析式及点，的坐标；

（2）点是轴上的动点，

①求的最大值及对应的点的坐标；

②设是轴上的动点，若线段与函数的图像只有一个公共点，求的取值范围.

22．（10分）知y+3与5x+4成正比例，当x=1时，y=—18，

（1）求y关于x的函数关系。

（2）若点（m，—8）在此图像上，求m的值。

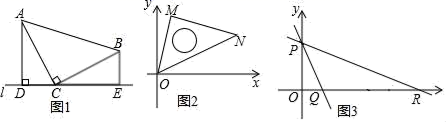
23．（12分）（1）探索发现：如图1，已知Rt△ABC中，∠ACB＝90°，AC＝BC，直线l过点C，过点A作AD⊥l，过点B作BE⊥l，垂足分别为D、E．求证：AD＝CE，CD＝BE．

（2）迁移应用：如图2，将一块等腰直角的三角板MON放在平面直角坐标系内，三角板的一个锐角的顶点与坐标原点O重合，另两个顶点均落在第一象限内，已知点M的坐标为（1，3），求点N的坐标．

（3）拓展应用：如图3，在平面直角坐标系内，已知直线y＝﹣3x+3与y轴交于点P，与x轴交于点Q，将直线PQ绕P点沿逆时针方向旋转45°后，所得的直线交x轴于点R．求点R的坐标．

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、D

2、D

3、B

4、A

5、A

6、C

7、B

8、C

9、B

10、B

11、C

12、C

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、对应角相等的三角形全等

14、120

15、1．

16、6

17、

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1）每辆中巴车有座位45个，每辆大客车有座位60个．（1）租用中巴车1辆和大客车3辆，比单独租用中巴车的租车费少100元，比单独租用大客车的租车费少100元．

19、（1）见解析；（2）.

20、（1）见解析；（1）①见解析，②1

21、（1），点坐标为，顶点的坐标为；（2）①最大值是，的坐标为，②的取值范围为或或.

22、 (1) y=x；
(2) m=.

23、（1）见解析（2）（4，2）（3）（6，0）