


2022-2023学年临汾市重点中学七下数学期末综合测试模拟试题含答案
展开
这是一份2022-2023学年临汾市重点中学七下数学期末综合测试模拟试题含答案,共7页。
2022-2023学年临汾市重点中学七下数学期末综合测试模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗. 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列直线与一次函数![]() 的图像平行的直线是( )A.
的图像平行的直线是( )A.![]() ; B.
; B.![]() ; C.
; C.![]() ; D.
; D.![]() .2.下列命题中,原命题和逆命题都是真命题的个数是( )①两条对角线互相平分的四边形是平行四边形;②两条对角线相等的四边形是矩形;③菱形的两条对角线成互相垂直平分;④两条对角线互相垂直且相等的四边形是正方形.A.4 B.3 C.2 D.13.函数
.2.下列命题中,原命题和逆命题都是真命题的个数是( )①两条对角线互相平分的四边形是平行四边形;②两条对角线相等的四边形是矩形;③菱形的两条对角线成互相垂直平分;④两条对角线互相垂直且相等的四边形是正方形.A.4 B.3 C.2 D.13.函数![]() 与
与![]() 在同一坐标系中的图象可能是( )A.
在同一坐标系中的图象可能是( )A.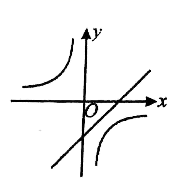 B.
B.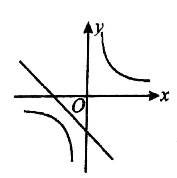 C.
C.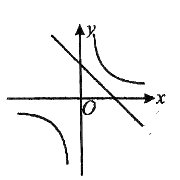 D.
D.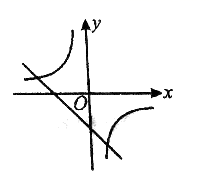 4.如图,在△ABC中,AB=AC=10,BC=12,点D是BC上一点,DE∥AC,DF∥AB,则△BED与△DFC的周长的和为( )
4.如图,在△ABC中,AB=AC=10,BC=12,点D是BC上一点,DE∥AC,DF∥AB,则△BED与△DFC的周长的和为( )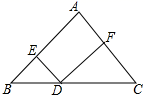 A.34 B.32 C.22 D.205.一组数据11、12、15、12、11,下列说法正确的是( )A.中位数是15 B.众数是12C.中位数是11、12 D.众数是11、126.下列各式由左边到右边的变形中,属于分解因式的是( )A.
A.34 B.32 C.22 D.205.一组数据11、12、15、12、11,下列说法正确的是( )A.中位数是15 B.众数是12C.中位数是11、12 D.众数是11、126.下列各式由左边到右边的变形中,属于分解因式的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 7.如图所示.在△ABC中,AC=BC,∠C=90°,AD平分∠CAB交BC于点D,DE⊥AB于点E,若AB=6 cm,则△DEB的周长为( )
7.如图所示.在△ABC中,AC=BC,∠C=90°,AD平分∠CAB交BC于点D,DE⊥AB于点E,若AB=6 cm,则△DEB的周长为( )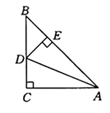 A.12 cm B.8 cm C.6 cm D.4 cm8.如图,直线y1=kx+2与直线y2=mx相交于点P(1,m),则不等式mx<kx+2的解集是( )
A.12 cm B.8 cm C.6 cm D.4 cm8.如图,直线y1=kx+2与直线y2=mx相交于点P(1,m),则不等式mx<kx+2的解集是( )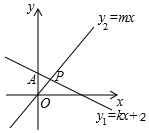 A.x<0 B.x<1 C.0<x<1 D.x>19.等式
A.x<0 B.x<1 C.0<x<1 D.x>19.等式![]() 成立的条件是( )A.
成立的条件是( )A.![]() B.
B.![]() C.x>2 D.
C.x>2 D.![]() 10.在同一平面直角坐标系中,函数
10.在同一平面直角坐标系中,函数![]() 与
与![]() 的图象大致是( )A.
的图象大致是( )A.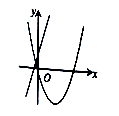 B.
B.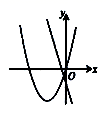 C.
C.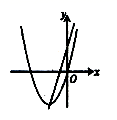 D.
D.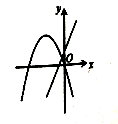 11.如图,在
11.如图,在![]() ABCD中,DE,BF分别是∠ADC和∠ABC的平分线,添加一个条件,仍无法判断四边形BFDE为菱形的是( )
ABCD中,DE,BF分别是∠ADC和∠ABC的平分线,添加一个条件,仍无法判断四边形BFDE为菱形的是( )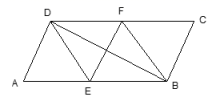 A.∠A=60˚ B.DE=DF C.EF⊥BD D.BD 是∠EDF的平分线12.如图,
A.∠A=60˚ B.DE=DF C.EF⊥BD D.BD 是∠EDF的平分线12.如图,![]() ,
,![]() 垂直平分线段
垂直平分线段![]() 于点
于点![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() 等于( )
等于( )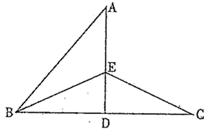 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,在平行四边形纸片ABCD中,AB=3,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形,则图中重叠部分的面积为_____.
二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,在平行四边形纸片ABCD中,AB=3,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形,则图中重叠部分的面积为_____.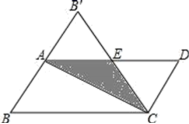 14.已知E是正方形ABCD的对角线AC上一点,AE=AD,过点E作AC的垂线,交边CD于点F,那么∠FAD=________度.15.如图,在边长为1的正方形网格中,两格点
14.已知E是正方形ABCD的对角线AC上一点,AE=AD,过点E作AC的垂线,交边CD于点F,那么∠FAD=________度.15.如图,在边长为1的正方形网格中,两格点![]() 之间的距离为
之间的距离为![]() __________1.(填“
__________1.(填“![]() ”,“
”,“ ![]() ”或“
”或“![]() ”).
”).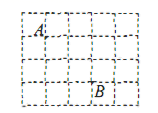 16.Rt△ABC中,∠C=90°,∠B=30°,则AC与AB两边的关系是_____.17.若点
16.Rt△ABC中,∠C=90°,∠B=30°,则AC与AB两边的关系是_____.17.若点![]() 与点
与点![]() 关于原点对称,则
关于原点对称,则![]() _______________.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
_______________.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.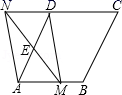 (1)求证:四边形AMDN是平行四边形.(2)当AM的值为何值时,四边形AMDN是矩形,请说明理由. 19.(5分)如图,在四边形ABCD中,∠D=90°,AB=13,BC=12,CD=4,AD=3.
(1)求证:四边形AMDN是平行四边形.(2)当AM的值为何值时,四边形AMDN是矩形,请说明理由. 19.(5分)如图,在四边形ABCD中,∠D=90°,AB=13,BC=12,CD=4,AD=3.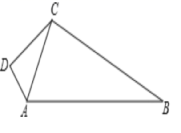 求:(1)AC的长度;(2)判断△ACB是什么三角形?并说明理由?(3)四边形ABCD的面积。 20.(8分)已知正比例函数
求:(1)AC的长度;(2)判断△ACB是什么三角形?并说明理由?(3)四边形ABCD的面积。 20.(8分)已知正比例函数![]() 与反比例函数
与反比例函数![]() .(1)证明:直线与双曲线没有交点;(2)若将直线
.(1)证明:直线与双曲线没有交点;(2)若将直线![]() 向上平移4个单位后与双曲线恰好有且只有一个交点,求反比例函数的表达式和平移后的直线表达式;(3)将(2)小题平移后的直线代表的函数记为
向上平移4个单位后与双曲线恰好有且只有一个交点,求反比例函数的表达式和平移后的直线表达式;(3)将(2)小题平移后的直线代表的函数记为![]() ,根据图象直接写出:对于负实数
,根据图象直接写出:对于负实数![]() ,当
,当![]() 取何值时
取何值时![]() 21.(10分)我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
21.(10分)我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)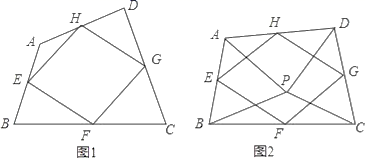 22.(10分)先化简再求值:(
22.(10分)先化简再求值:(![]() )÷
)÷![]() ,其中x=11﹣
,其中x=11﹣![]() . 23.(12分)一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示:销售方式
. 23.(12分)一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示:销售方式
粗加工后销售
精加工后销售
每吨获利(元)
1000
2000
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?(2)如果先进行精加工,然后进行粗加工.①试求出销售利润![]() 元与精加工的蔬菜吨数
元与精加工的蔬菜吨数![]() 之间的函数关系式;②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间? 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、B2、C3、D4、B5、D6、B7、C8、B9、C10、C11、A12、A 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、
之间的函数关系式;②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间? 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、B2、C3、D4、B5、D6、B7、C8、B9、C10、C11、A12、A 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、![]() .14、
.14、![]() 15、<16、AB=2AC.17、
15、<16、AB=2AC.17、![]() 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)证明见解析;(2)AM=1.理由见解析.19、(1)5(2)直角三角形,理由见解析(3)3620、(1)方程组无解即没有公共解,也就是两函数图象没有交点(交点即公共点);(2)当
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)证明见解析;(2)AM=1.理由见解析.19、(1)5(2)直角三角形,理由见解析(3)3620、(1)方程组无解即没有公共解,也就是两函数图象没有交点(交点即公共点);(2)当![]() 时,
时,![]()
![]() 当
当![]() 时,
时,![]()
![]() ;(3)当
;(3)当![]() 或
或![]() 时满足
时满足![]() .21、(1)证明见解析;(2)四边形EFGH是菱形,证明见解析;(3)四边形EFGH是正方形.22、12﹣
.21、(1)证明见解析;(2)四边形EFGH是菱形,证明见解析;(3)四边形EFGH是正方形.22、12﹣![]() .23、(1)应安排4天进行精加工,8天进行粗加工(2)①
.23、(1)应安排4天进行精加工,8天进行粗加工(2)①![]() =
=![]() ②安排1天进行精加工,9天进行粗加工,可以获得最多利润为
②安排1天进行精加工,9天进行粗加工,可以获得最多利润为![]() 元
元
相关试卷
这是一份黄南市重点中学2022-2023学年数学七下期末综合测试模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,一元二次方程配方后可变形为等内容,欢迎下载使用。
这是一份酒泉市重点中学2022-2023学年数学七下期末综合测试试题含答案,共7页。
这是一份衢州市重点中学2022-2023学年数学七下期末综合测试模拟试题含答案,共7页。试卷主要包含了下列说法中,错误的是,下列各组长度的线段等内容,欢迎下载使用。










