2021届江苏省淮安市淮阴中学高三上学期期中模拟测试数学试题

淮阴中学2020/2021学年度第一学期期中模拟试卷

高三数学

一、选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的。

１.已知集合，则等于（    ）

A．           B．

C．　　　   　 D．

2．已知向量，则等于 （    ）

A．         B．         C．25           D．5

３．长方体的长、宽、高分别为3、2、1，则从A到沿长方体的表面的最短距离为              （    ）

A．　　　　B．　 C．　 D．

４.已知函数，则对任意，若，下列不等式成立的是                                                              （    ）

A.            B. 

C.            D. 

５．三个共面向量、、两两所成的角相等，且，，，则 等于                                                     （    ）

A．            B．6           C．或6    D．3或6

６．正方形的边长为2，点、分别在边、上，且，，将此正方形沿、折起，使点、重合于点，则三棱锥的体积是

A．            B．       C．     D．

７.函数的零点所在的区间为            (    )

A．    B．(     C．     D．

８.设点P是椭圆上的一点，点M、N分别是两圆：和上的点，则的最小值、最大值分别为                (    )

  A. 4，8        B.2，6          C)  6，8      D.8，12

二、多项选择题：本题共４小题，每小题５分，共２０分，在每小题给出的选项中，有多项符合要求，全部选对的得５分，部分选对的得３分，有选错的得０分）

９.若函数f(x)具有性质:,则称f(x)是满足“倒负”变换的函数.下列四个函数: 其中,满足“倒负”变换的所有函数的选项是            (    )

A.(a>0且a≠1);        B.(a>0且a≠1);

C.;                      D..

10.定义在上的偶函数在[—1，0]上是增函数，给出下列关于的判断: 其中正确的选项是            (    )

A．关于直线对称；　　　　　　　　　B．是[0，1]上是增函数；

Ｃ．在[1，2]上是减函数；　　　　　　　　　Ｄ．．

11．设、是不同的直线，、、是不同的平面，有以下四个命题：

A ．      B．

C．      D．，其中正确的选项是         (    )

（A）（1）（2） （B）（1）（3）　  

（C）（2）（3） （D）（2）（4） 

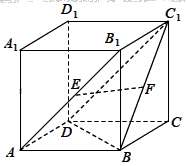
12.如图所示，在长方体，若，，分别是，的中点，则下列结论中不成立的是（    ）

A. 与垂直 B. 平面

C. 与所成的角为45° D. 平面

三、填空题：本大题共４小题，每小题5分，共２0分，请将答案填在题中横线上

1３．已知  则的最小值是______． 

14．已知F是双曲线的左焦点，是双曲线右支上的动点，则的最小值为          .

15．用0，1，2，3，4这五个数字组成无重复数字的五位数，其中恰有一个偶数夹在两个奇数之间的五位数共有       

16．圆柱形容器的内壁底半径是cm，有一个实心铁球浸没于容器的水中，若取出这个铁球，测得容器的水面下降了cm，则这个铁球的表面积为          .

四、解答题：本大题共６个小题 共70分

17． 设条件：实数满x2—4ax+3a2<0(a>0)条件：实数满足; 已知q是p的必要不充分条件，求实数的取值范围。

18已知向量（＞0），函数的最小正周期为。

（I）求函数的单调增区间；

（II）如果△ABC的三边a、b、c所对的角分别为A、B、C，且满足求的值。

19.某地有三个村庄，分别位于等腰直角三角形ABC的三个顶点处，已知AB=AC=18km，现计划在BC边的高AO上一点P处建造一个变电站. 记P到三个村庄的距离之和为y ，（1）设，把y表示成的函数关系式；（2）变电站建于何处时，它到三个小区的距离之和最小？

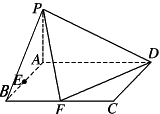20. 已知四棱锥底面ABCD是矩形，PA⊥平面ABCD，AD＝2，AB＝1，E．F分别是线段AB，BC的中点，

（Ⅰ）证明：PF⊥FD；

（Ⅱ）在PA上找一点G，使得EG∥平面PFD；．

（Ⅲ）若与平面所成的角为，求二面角的余弦值．

21.已知函数,(其中).

（Ⅰ）求曲线在处的切线方程;

（Ⅱ）若是函数的极值点，求实数的值;

（Ⅲ）若对任意的，（为自然对数的底数，）都有，求实数的取值范围.

22.已知数列的前n项和为，且满足，．

（Ⅰ）问：数列是否为等差数列？并证明你的结论；

（Ⅱ）求和；

（Ⅲ）求证：．

参考答案

选择题答案

01-05 CDCDC    06-08 BBA   09 ACD  10 AD  11 AC  12ＡＢＤ

填空题答案

13  5      14    9    15  28    16   100π

解答题

17. 解：设，可解得：，

    设可解得：，

  ∵q是的必要不充分条件

 。

18.

 解析：（I）

∵的最小正周期为，且＞0。

∴∴

∴

由≤≤

得的增区间为

（II）由∴

又由

∴在中，

∴

19、解：（1）由等腰直角三角形ABC中AB=AC=18km得： =OA=km， 

又，所以.

 所以点P到A、B、C的距离之和为

故所求函数关系式为.   ()  

答：变电站建于距O点3km处时，它到三个小区的距离之和最小.

20. 解：（Ⅰ）证明：连接AF，则AF＝，DF＝，

又AD＝2，∴DF2＋AF2＝AD2，

∴DF⊥AF．又PA⊥平面ABCD，

∴DF⊥PA，又PA∩AF＝A，

（Ⅱ）过点E作EH∥FD交AD于点H，则EH∥平面PFD且AH＝A 

再过点H作HG∥DP交PA于点G，则HG∥平面PFD且AG＝AP，

∴平面EHG∥平面PF 

∴EG∥平面PF D．

从而满足AG＝AP的点G为所求．                      

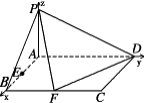
（Ⅲ）建立如图所示的空间直角坐标系，因为PA⊥平面ABCD ，所以是与平面所成的角．

又有已知得，所以，所以

．

设平面的法向量为，由

得，令，解得：．

所以．

又因为，

所以是平面的法向量，

易得，

所以．

由图知，所求二面角的余弦值为．   

21. 解：（Ⅰ）

定义域

，

法一：令，解得，

又，，

经验证符合条件.

法二：令，，

，，为极值点，

，解得，又，，

（Ⅱ）对任意的都有成立，

等价于对任意的都有成立，

当，，在上单调递增，

. ，，

（1）若，，

在单调递增，

， ，解得.

（2）若

当，则

当，则

在递减，在递增，，

，又，

（3）当时， 在递减，

，恒成立.  

综上所述.

22．