高考数学一轮复习课时作业：68 离散型随机变量及其分布列 Word版含解析

课时作业68　离散型随机变量及其分布列

一、选择题

1．袋中装有10个红球、5个黑球．每次随机抽取1个球后，若取得黑球则另换1个红球放回袋中，直到取到红球为止．若抽取的次数为X，则表示“放回5个红球”事件的是(　C　)

A．X＝4  B．X＝5

C．X＝6  D．X≤5

解析：事件“放回5个红球”表示前5次摸到黑球，且第6次摸到红球，所以X＝6.

2．设随机变量Y的分布列为

则“≤Y≤”的概率为(　C　)

A.   B.

C.   D.

解析：依题意知，＋m＋＝1，则m＝.故P＝P(Y＝2)＋P(Y＝3)＝＋＝.

3．已知离散型随机变量X的分布列为

则P(∈Z)＝(　A　)

A．0.9  B．0.8

C．0.7  D．0.6

解析：由分布列性质得0.5＋1－2q＋q＝1，解得q＝0.3，∴P(∈Z)＝P(X＝0)＋P(X＝1)＝0.5＋1－2×0.3＝0.9.故选A.

4．若P(X≤x2)＝1－β，P(X≥x1)＝1－α，其中x1<x2，则P(x1≤X≤x2)等于(　B　)

A．(1－α)(1－β)  B．1－(α＋β)

C．1－α(1－β)  D．1－β(1－α)

解析：显然P(X>x2)＝β，P(X<x1)＝α.由概率分布列的性质可知P(x1≤X≤x2)＝1－P(X>x2)－P(X<x1)＝1－α－β.

5．已知在10件产品中可能存在次品，从中抽取2件检查，其次品数为ξ，已知P(ξ＝1)＝，且该产品的次品率不超过40%，则这10件产品的次品率为(　B　)

A．10%  B．20%

C．30%  D．40%

解析：设10件产品中有x件次品，则P(ξ＝1)＝＝＝，∴x＝2或8.∵次品率不超过40%，∴x＝2，∴次品率为＝20%.

6．一只袋内装有m个白球，n－m个黑球，连续不放回地从袋中取球，直到取出黑球为止，设此时取出了X个白球，下列概率等于的是(　D　)

A．P(X＝3)  B．P(X≥2)

C．P(X≤3)  D．P(X＝2)

解析：由超几何分布知P(X＝2)＝.

二、填空题

7．甲、乙两队在一次对抗赛的某一轮中有3个抢答题，比赛规定：对于每一个题，没有抢到题的队伍得0分，抢到题并回答正确的得1分，抢到题但回答错误的扣1分(即得－1分)．若X是甲队在该轮比赛获胜时的得分(分数高者胜)，则X的所有可能取值是－1,0,1,2,3.

解析：X＝－1，甲抢到一题但答错了．

X＝0，甲没抢到题，或甲抢到2题，回答时一对一错．

X＝1时，甲抢到1题且答对或甲抢到3题，且一错两对．

X＝2时，甲抢到2题均答对．

X＝3时，甲抢到3题均答对．

8．从4名男生和2名女生中任选3人参加演讲比赛，则所选3人中女生人数不超过1人的概率是.

解析：设所选女生人数为X，则X服从超几何分布，其中N＝6，M＝2，n＝3，则P(X≤1)＝P(X＝0)＋P(X＝1)＝＋＝.

9．(2019·石家庄调研)为检测某产品的质量，现抽取5件产品，测量产品中微量元素x，y的含量(单位：毫克)，测量数据如下：

如果产品中的微量元素x，y满足x≥175且y≥75时，该产品为优等品．

现从上述5件产品中，随机抽取2件，则抽取的2件产品中优等品数X的分布列为

解析：5件抽测品中有2件优等品，则X的可能取值为0,1,2.

P(X＝0)＝＝0.3，

P(X＝1)＝＝0.6，

P(X＝2)＝＝0.1.

故优等品数X的分布列为

三、解答题

10．某小组共10人，利用假期参加义工活动，已知参加义工活动次数为1,2,3的人数分别为3,3,4.现从这10人中随机选出2人作为该组代表参加座谈会．

(1)设A为事件“选出的2人参加义工活动次数之和为4”，求事件A发生的概率．

(2)设X为选出的2人参加义工活动次数之差的绝对值，求随机变量X的分布列．

解：(1)由已知事件A：选出的2人参加义工活动次数之和为4，则P(A)＝＝.

(2)随机变量X可能的取值为0,1,2，

P(X＝0)＝＝，

P(X＝1)＝＝，

P(X＝2)＝＝，

则X的分布列为：

11．为推动乒乓球运动的发展，某乒乓球比赛允许不同协会的运动员组队参加．现有来自甲协会的运动员3名，其中种子选手2名；乙协会的运动员5名，其中种子选手3名．从这8名运动员中随机选择4人参加比赛．

(1)设A为事件“选出的4人中恰有2名种子选手，且这2名种子选手来自同一个协会”，求事件A发生的概率；

(2)设X为选出的4人中种子选手的人数，求随机变量X的分布列．

解：(1)由已知，有P(A)＝＝.所以事件A发生的概率为.

(2)随机变量X的所有可能取值为1,2,3,4.

P(X＝k)＝(k＝1,2,3,4)．

故P(X＝1)＝＝，

P(X＝2)＝＝，

P(X＝3)＝＝，

P(X＝4)＝＝，

所以随机变量X的分布列为

12．设ξ为随机变量，从棱长为1的正方体的12条棱中任取两条，当两条棱相交时，ξ＝0；当两条棱平行时，ξ的值为两条棱之间的距离；当两条棱异面时，ξ＝1，则随机变量ξ的分布列是

 .

解析：若两条棱相交，则交点必为正方体8个顶点中的1个，过任意1个顶点恰有3条棱，所以共有8C对相交棱，因此P(ξ＝0)＝＝＝.

若两条棱平行，则它们的距离为1或，其中距离为的共有6对，故P(ξ＝)＝＝，于是P(ξ＝1)＝1－P(ξ＝0)－P(ξ＝)＝1－－＝，

所以随机变量ξ的分布列是

13.(2019·河南豫南九校联考)为创建国家级文明城市，某城市号召出租车司机在高考期间至少进行一次“爱心送考”，该城市某出租车公司共200名司机，他们进行“爱心送考”的次数统计如图所示．

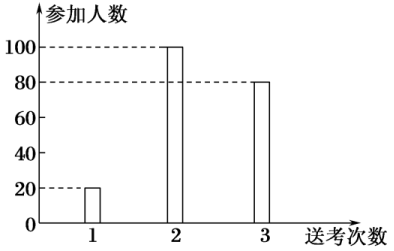
(1)求该出租车公司的司机进行“爱心送考”的人均次数；

(2)从这200名司机中任选两人，设这两人进行送考次数之差的绝对值为随机变量X，求X的分布列及数学期望．

解：(1)由统计图得200名司机中送考1次的有20人，送考2次的有100人，送考3次的有80人，

∴该出租车公司的司机进行“爱心送考”的人均次数为＝2.3.

(2)从该公司任选两名司机，记“这两人中一人送考1次，另一人送考2次”为事件A，

“这两人中一人送考2次，另一人送考3次”为事件B，

“这两人中一人送考1次，另一人送考3次”为事件C，

“这两人送考次数相同”为事件D，

由题意知X的所有可能取值为0,1,2，

P(X＝1)＝P(A)＋P(B)

＝＋＝，

P(X＝2)＝P(C)＝＝，

P(X＝0)＝P(D)＝＝，

∴X的分布列为

E(X)＝0×＋1×＋2×＝.

14．甲、乙两人为了响应政府“节能减排”的号召，决定各购置一辆纯电动汽车．经了解目前市场上销售的主流纯电动汽车，按行驶里程数R(单位：公里)可分为三类车型，A：80≤R<150，B：150≤R<250，C：R≥250.甲从A，B，C三类车型中挑选，乙从B，C两类车型中挑选，甲、乙二人选择各类车型的概率如下表：

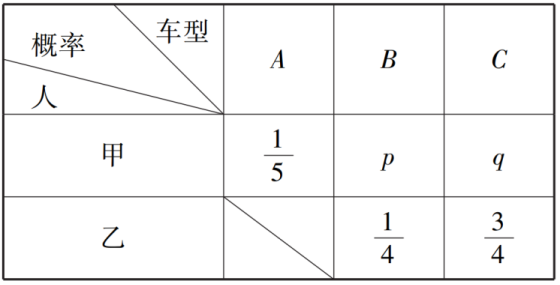
若甲、乙都选C类车型的概率为.

(1)求p，q的值；

(2)求甲、乙选择不同车型的概率；

(3)某市对购买纯电动汽车进行补贴，补贴标准如下表：

记甲、乙两人购车所获得的财政补贴和为X，求X的分布列．

解：(1)由题意可知

解得p＝，q＝.

(2)设“甲、乙选择不同车型”为事件A，则P(A)＝＋×＋×＝，所以甲、乙选择不同车型的概率是.

(3)X可能取值为7,8,9,10.

P(X＝7)＝×＝，

P(X＝8)＝×＋×＝，

P(X＝9)＝×＋×＝，

P(X＝10)＝×＝.

所以X的分布列为：