尺规作图-(-中考数学复习)课件PPT

这是一份尺规作图-(-中考数学复习)课件PPT，共43页。

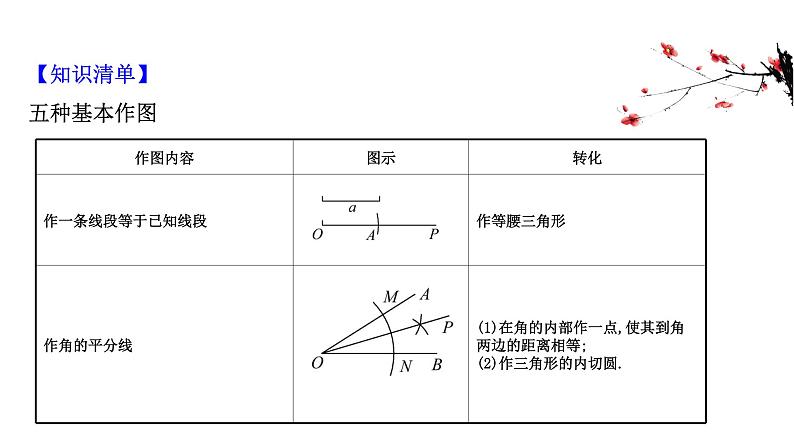
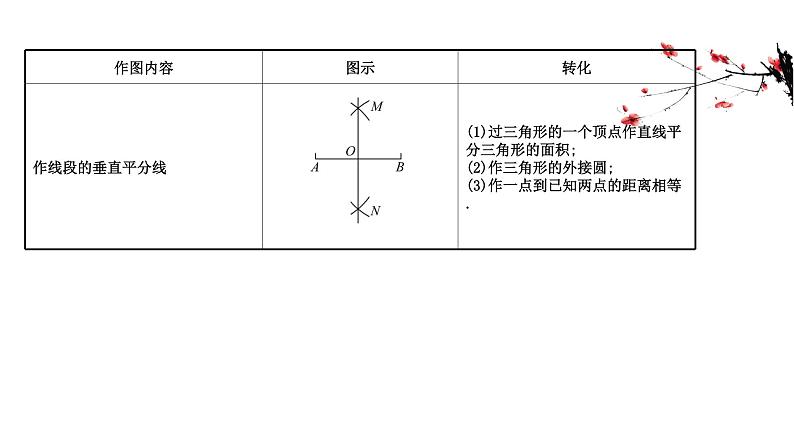
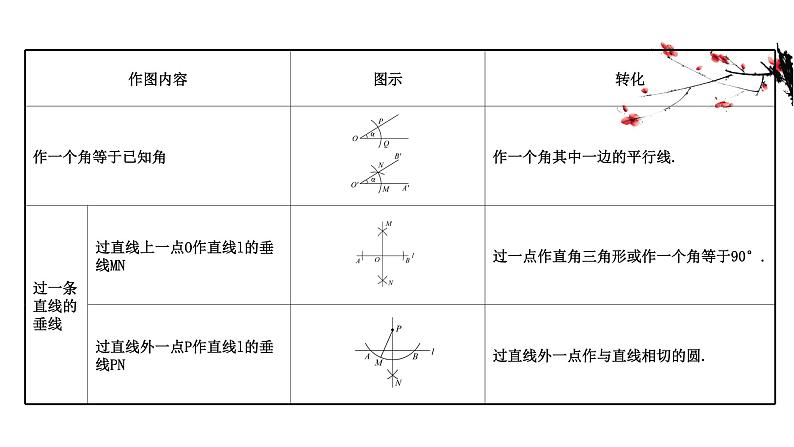
【知识清单】五种基本作图
【特别提醒】常用的作图语言:(1)过点×,×作线段或射线、直线;(2)连接两点×,×;(3)在线段××或射线××上截取××=××;(4)以点×为圆心,以××的长为半径作圆(或画弧),交××于点×;(5)分别以点×,点×为圆心,以××,××的长为半径作弧,两弧相交于点×;(6)延长××到点×,使××=××.
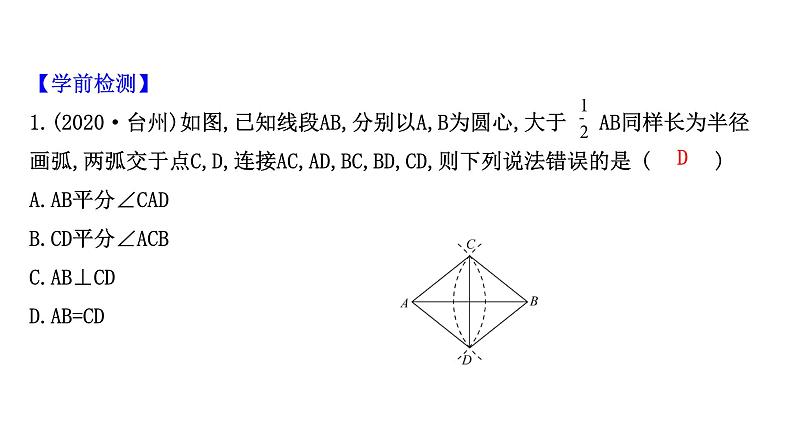
【学前检测】 1.(2020·台州)如图,已知线段AB,分别以A,B为圆心,大于 AB同样长为半径画弧,两弧交于点C,D,连接AC,AD,BC,BD,CD,则下列说法错误的是(　 　)A.AB平分∠CADB.CD平分∠ACBC.AB⊥CDD.AB=CD
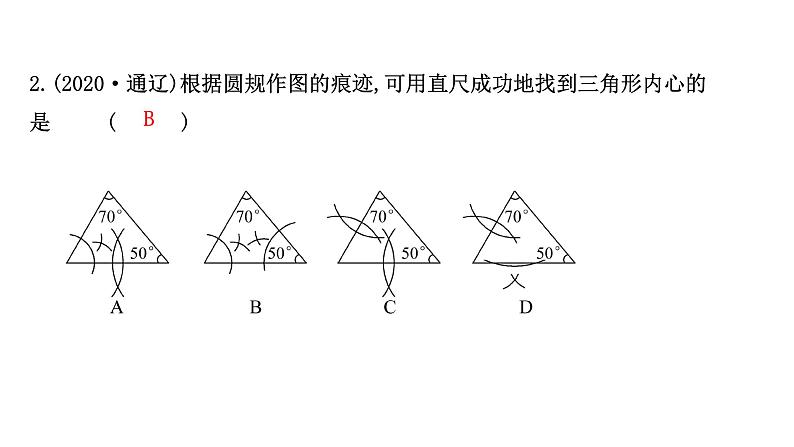
2.(2020·通辽)根据圆规作图的痕迹,可用直尺成功地找到三角形内心的是(　 　)
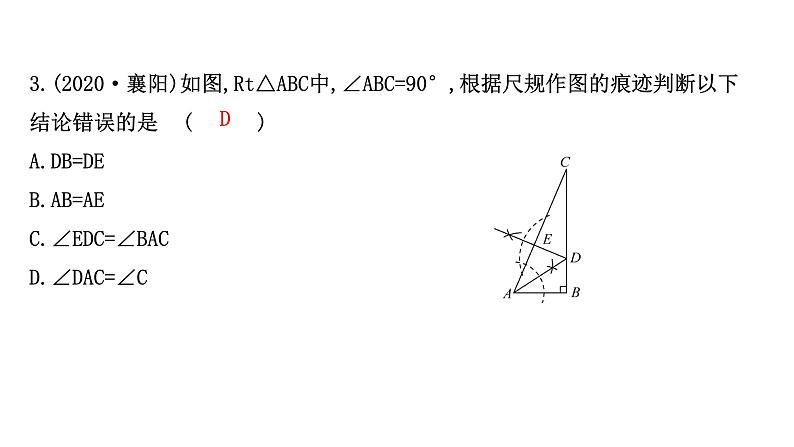
3.(2020·襄阳)如图,Rt△ABC中,∠ABC=90°,根据尺规作图的痕迹判断以下结论错误的是(　 　)A.DB=DEB.AB=AEC.∠EDC=∠BACD.∠DAC=∠C
4.(2020·贵阳)如图,Rt△ABC中,∠C=90°,利用尺规在BC,BA上分别截取BE,BD,使BE=BD;分别以D,E为圆心、以大于 DE的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G.若CG=1,P为AB上一动点,则GP的最小值为(　 　)A.无法确定B. C.1D.2
5.(2020·河北)如图1,已知∠ABC,用尺规作它的角平分线.如图2,步骤如下,第一步:以B为圆心,以a为半径画弧,分别交射线BA,BC于点D,E;第二步:分别以D,E为圆心,以b为半径画弧,两弧在∠ABC内部交于点P;第三步:画射线BP.射线BP即为所求.下列正确的是(　 　)A.a,b均无限制B.a>0,b> DE的长C.a有最小限制,b无限制D.a≥0,b< DE的长
【联系课标】【课标要求】(1)会用尺规作一条线段等于已知线段,尺规作图题会写已知,求作和作法(不要求证明)(2)会用尺规作一个角等于已知角,作角的平分线(3)会用尺规作已知线段的垂直平分线(4)会利用基本作图作三角形:已知两边及其夹角作三角形;已知两角及其夹边作三角形;已知三边作三角形(5)会用尺规作图:已知底边及底边上的高作等腰三角形
【考点剖析】 【考点1】尺规作图、计算及证明例1.(2020·扬州)如图,在△ABC中,按以下步骤作图:①以点B为圆心,任意长为半径作弧,分别交AB,BC于点D,E;②分别以点D,E为圆心,大于 DE的同样长为半径作弧,两弧交于点F;③作射线BF交AC于点G.如果AB=8,BC=12,△ABG的面积为18,求△CBG的面积.
【解析】如图,过点G作GM⊥AB于点M,GN⊥BC于点N,根据作图过程可知:BG是∠ABC的平分线,∴GM=GN,∵△ABG的面积为18,∴ AB×GM=18,∴4GM=18,∴GM= ,∴△CBG的面积为: BC×GN= ×12× =27.
变式1.(2020·辽阳)如图,在Rt△ABC中,∠ACB=90°,AC=2BC,分别以点A和B为圆心,以大于 AB的长为半径作弧,两弧相交于点M和N,作直线MN,交AC于点E,连接BE,若CE=3,求BE的长.
【解析】由作图可知,MN垂直平分线段AB,∴AE=EB,设AE=EB=x,∵EC=3,AC=2BC,∴BC= (x+3),在Rt△BCE中,∵BE2=BC2+EC2,∴x2=32+ ,解得,x=5或-3(舍弃),∴BE=5.
变式2.(2020·长沙)人教版初中数学教科书八年级上册第48页告诉我们一种作已知角的平分线的方法:已知:∠AOB.求作:∠AOB的平分线.作法:(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N;(2)分别以点M,N为圆心,大于 MN的长为半径画弧,两弧在∠AOB的内部相交于点C;
(3)画射线OC,射线OC即为所求(如图).请你根据提供的材料完成下面问题.(1)这种作已知角的平分线的方法的依据是　　　　;(填序号) ①SSS;②SAS;③AAS;④ASA.(2)请你证明OC为∠AOB的平分线.
【解析】(1)这种作已知角的平分线的方法的依据是①SSS.答案:①(2)由基本作图方法可得:OM=ON,OC=OC,MC=NC,则在△OMC和△ONC中, ∴△OMC≌△ONC(SSS),∴∠AOC=∠BOC,即OC为∠AOB的平分线.反思:利用尺规作图的基本方法,寻找相等的线段、角.
【考点2】网格中的作图例2.(2020·哈尔滨)如图,方格纸中每个小正方形的边长均为1,线段AB和线段CD的端点均在小正方形的顶点上.
(1)在图中画出以AB为边的正方形ABEF,点E和点F均在小正方形的顶点上;(2)在图中画出以CD为边的等腰三角形CDG,点G在小正方形的顶点上,且△CDG的周长为10+ .连接EG,请直接写出线段EG的长.
【解析】(1)如图,正方形ABEF即为所求.(2)如图,△CDG即为所求.连接EG,EG= .
变式1.(2020·武汉)在8×5的网格中建立如图的平面直角坐标系,四边形OABC的顶点坐标分别为O(0,0),A(3,4),B(8,4),C(5,0).仅用无刻度的直尺在给定网格中按下列步骤完成画图,并回答问题:
(1)将线段CB绕点C逆时针旋转90°,画出对应线段CD;(2)在线段AB上画点E,使∠BCE=45°(保留画图过程的痕迹);(3)连接AC,画点E关于直线AC的对称点F,并简要说明画法.
【解析】(1)如图所示:线段CD即为所求;(2)如图所示:∠BCE即为所求;(3)连接(5,0),(0,5),可得与OA的交点F,点F即为所求,如图所示:
变式2.(2020·吉林)图①、图②、图③都是3×3的正方形网格,每个小正方形的顶点称为格点.A,B,C均为格点.在给定的网格中,按下列要求画图:
(1)在图①中,画一条不与AB重合的线段MN,使MN与AB关于某条直线对称,且M,N为格点.(2)在图②中,画一条不与AC重合的线段PQ,使PQ与AC关于某条直线对称,且P,Q为格点.(3)在图③中,画一个△DEF,使△DEF与△ABC关于某条直线对称,且D,E,F为格点.
【解析】(1)如图①,MN即为所求;(2)如图②,PQ即为所求;(3)如图③,△DEF即为所求.
反思:1.对称作图的基本步骤:找出原图形的关键点⇨作出关键点关于对称轴(或对称中心)的对应点⇨按照原图形依次连接得到的各关键点的对应点,得到对称后的图形.2.平移作图的基本步骤:确定平移方向和平移距离⇨找出原图形的关键点⇨按平移方向和平移距离,平移各个关键点,得到各关键点的对应点⇨按原图形依次连接得到的各关键点的对应点,得到平移后的图形.3.旋转作图的基本步骤:确定旋转的方向和旋转的角度⇨找出原图形的关键点⇨连接关键点与旋转中心,按旋转方向与旋转角将它们旋转,得到各关键点的对应点⇨按原图形依次连接得到的各关键点的对应点,得到旋转后的图形.
【考点3】尺规作图拓展应用例3.(2020·苏州)如图,已知∠MON是一个锐角,以点O为圆心,任意长为半径画弧,分别交OM,ON于点A,B,再分别以点A,B为圆心,大于 AB长为半径画弧,两弧交于点C,画射线OC.过点A作AD∥ON,交射线OC于点D,过点D作DE⊥OC,交ON于点E.设OA=10,DE=12,求sin ∠MON的值.
【解析】如图,连接AB交OD于点H,过点A作AG⊥ON于点G,由尺规作图步骤,可得:OD是∠MON的平分线,OA=OB,∴OH⊥AB,AH=BH,∵DE⊥OC,∴DE∥AB,∵AD∥ON,∴四边形ABED是平行四边形,∴AB=DE=12,∴AH=6,∴OH= =8,∵OB·AG=AB·OH,∴AG= ,∴sin ∠MON= .
变式1.(2020·郴州)如图,在矩形ABCD中,AD=4,AB=8.分别以点B,D为圆心,以大于 BD的长为半径画弧,两弧相交于点E和F.作直线EF分别与DC,DB,AB交于点M,O,N,则MN=_______. 
变式2.(2020·泰州)如图,已知线段a,点A在平面直角坐标系xOy内.(1)用直尺和圆规在第一象限内作出点P,使点P到两坐标轴的距离相等,且与点A的距离等于a.(保留作图痕迹,不写作法)(2)在(1)的条件下,若a≈2 ,A点的坐标为(3,1),求P点的坐标.
【解析】(1)如图,点P即为所求;
(2)由(1)可得OP是角平分线,设点P(x,x),过点P作PE⊥x轴于点E,过点A作AF⊥x轴于点F,AD⊥PE于点D,∵PA=a≈2 ,A点的坐标为(3,1),∴PD=x-1,AD=x-3,根据勾股定理,得PA2=PD2+AD2,∴(2 )2=(x-1)2+(x-3)2,解得x1=5,x2=-1(舍去).所以P点的坐标为(5,5).反思:利用尺规作图的基本方法,得出相等的线段、角进行推理计算.
【学后检测】 1.(2020·北部湾)如图,在△ABC中,BA=BC,∠B=80°,观察图中尺规作图的痕迹,则∠DCE的度数为(　 　)A.60°B.65°C.70°D.75°
2.(2020·新疆)如图,在x轴,y轴上分别截取OA,OB,使OA=OB,再分别以点A,B为圆心,以大于 AB长为半径画弧,两弧交于点P.若点P的坐标为(a,2a-3),则a的值为______. 
3.(2020·宁夏)如图,在△ABC中,∠C=84°,分别以点A,B为圆心,以大于 AB的长为半径画弧,两弧分别交于点M,N,作直线MN交AC于点D;以点B为圆心,适当长为半径画弧,分别交BA,BC于点E,F,再分别以点E,F为圆心,大于 EF的长为半径画弧,两弧交于点P,作射线BP,此时射线BP恰好经过点D,则∠A=_______度. 
4.(2020·北京)已知:如图,△ABC为锐角三角形,AB=AC,CD∥AB.求作:线段BP,使得点P在直线CD上,且∠ABP= ∠BAC.作法:①以点A为圆心,AC长为半径画圆,交直线CD于C,P两点;②连接BP.线段BP就是所求作线段.(1)使用直尺和圆规,依作法补全图形.(保留作图痕迹)
(2)完成下面的证明.证明:∵CD∥AB,∴∠ABP=　　　　. ∵AB=AC,∴点B在☉A上.又∵∠BPC= ∠BAC(　　　　)(填推理依据) ∴∠ABP= ∠BAC.
【解析】(1)如图所示, (2)∠BPC　在同圆或等圆中同弧所对的圆周角等于它所对圆心角的一半
5.(2020·福建)如图,C为线段AB外一点.(1)求作四边形ABCD,使得CD∥AB,且CD=2AB;(要求:尺规作图,不写作法,保留作图痕迹)(2)在(1)的四边形ABCD中,AC,BD相交于点P,AB,CD的中点分别为M,N,求证:M,P,N三点在同一条直线上.
【解析】(1)则四边形ABCD就是所求作的四边形.