
2023年黑龙江省大庆市中考数学试卷(含解析)
展开2023年黑龙江省大庆市中考数学试卷
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1. 实数2023的相反数是( )
A. 2023 B. −2023 C. 12023 D. −12023
2. 搭载神舟十六号载人飞船的长征二号F遥十六运载火箭于2023年5月30日成功发射升空,景海鹏、朱杨柱、桂海潮3名航天员开启“太空出差”之旅,展现了中国航天科技的新高度.下列图标中,其文字上方的图案是中心对称图形的是( )
A. B.
C. D.
3. 大庆油田发现预测地质储量12.68亿吨的页岩油,这标志着我国页岩油勘探开发取得重大战略突破.数字1268000000用科学记数法表示为( )
A. 1.268×109 B. 1.268×108 C. 1.268×107 D. 1.268×106
4. 一个长方体被截去一部分后,得到的几何体如图水平放置,其俯视图是( )
A.
B.
C.
D.
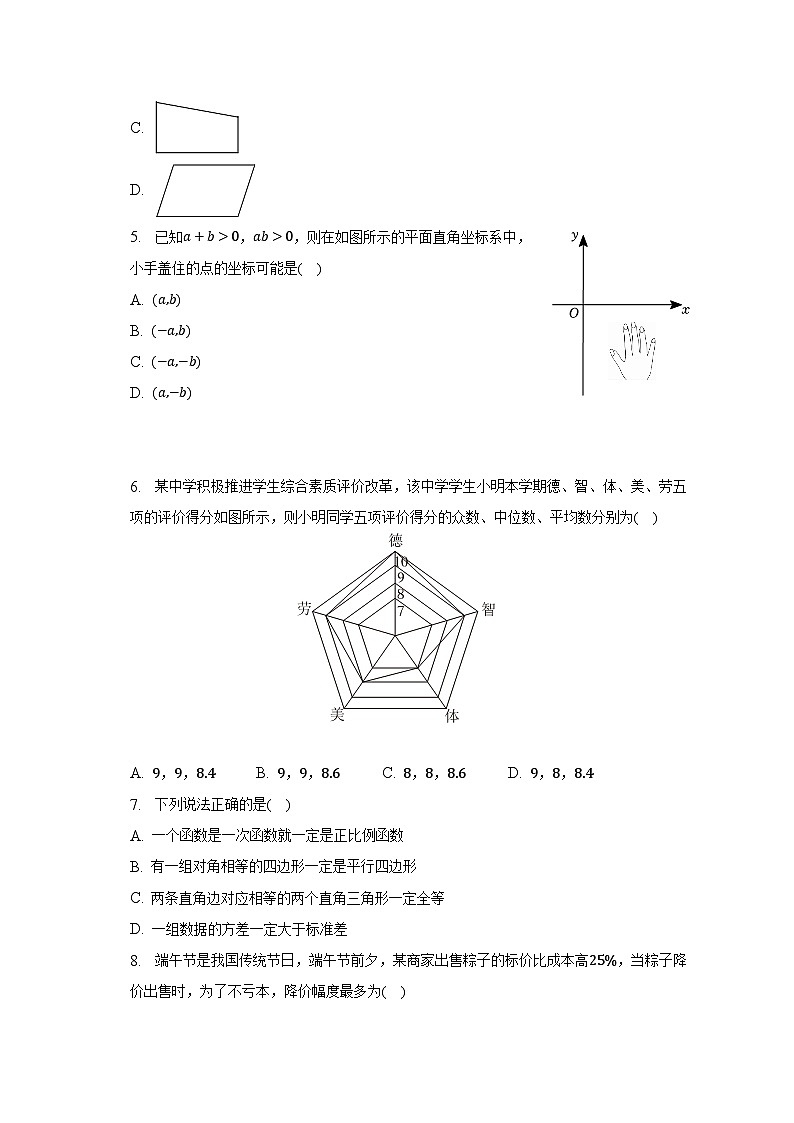
5. 已知a+b>0,ab>0,则在如图所示的平面直角坐标系中,小手盖住的点的坐标可能是( )
A. (a,b)
B. (−a,b)
C. (−a,−b)
D. (a,−b)
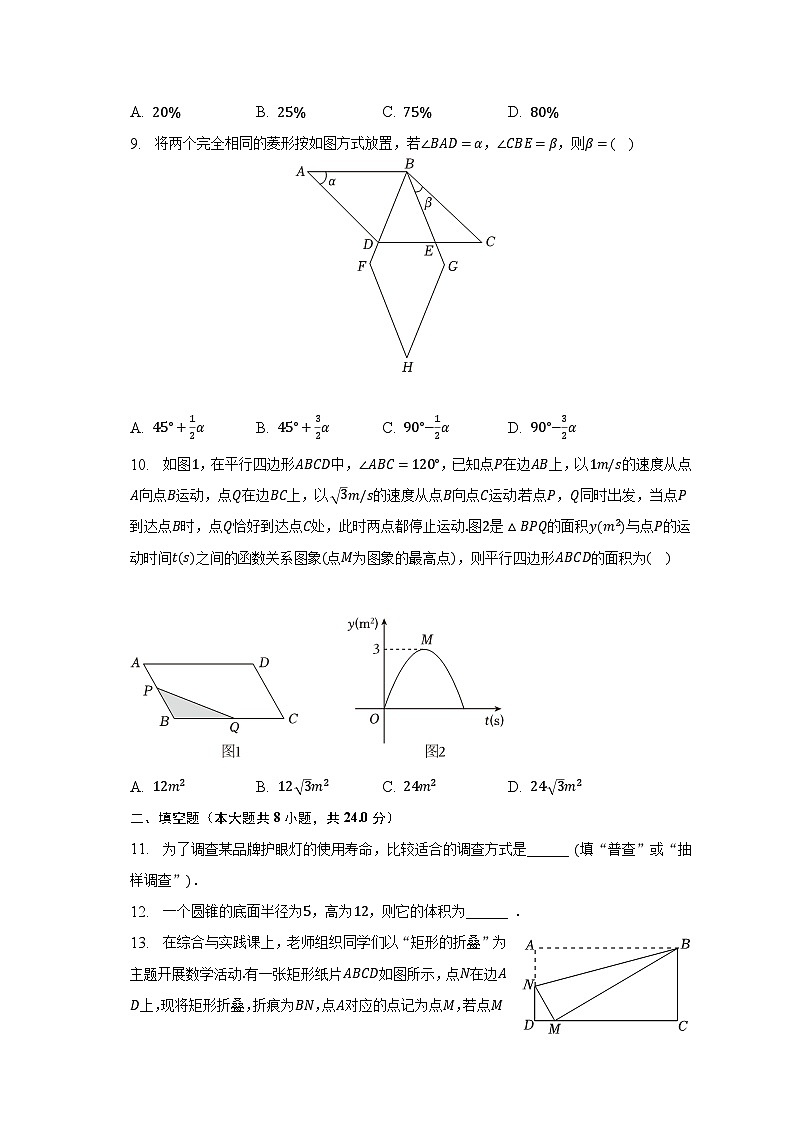
6. 某中学积极推进学生综合素质评价改革,该中学学生小明本学期德、智、体、美、劳五项的评价得分如图所示,则小明同学五项评价得分的众数、中位数、平均数分别为( )
A. 9,9,8.4 B. 9,9,8.6 C. 8,8,8.6 D. 9,8,8.4
7. 下列说法正确的是( )
A. 一个函数是一次函数就一定是正比例函数
B. 有一组对角相等的四边形一定是平行四边形
C. 两条直角边对应相等的两个直角三角形一定全等
D. 一组数据的方差一定大于标准差
8. 端午节是我国传统节日,端午节前夕,某商家出售粽子的标价比成本高25%,当粽子降价出售时,为了不亏本,降价幅度最多为( )
A. 20% B. 25% C. 75% D. 80%
9. 将两个完全相同的菱形按如图方式放置,若∠BAD=α,∠CBE=β,则β=( )
A. 45°+12α B. 45°+32α C. 90°−12α D. 90°−32α
10. 如图1,在平行四边形ABCD中,∠ABC=120°,已知点P在边AB上,以1m/s的速度从点A向点B运动,点Q在边BC上,以 3m/s的速度从点B向点C运动.若点P,Q同时出发,当点P到达点B时,点Q恰好到达点C处,此时两点都停止运动.图2是△BPQ的面积y(m2)与点P的运动时间t(s)之间的函数关系图象(点M为图象的最高点),则平行四边形ABCD的面积为( )
A. 12m2 B. 12 3m2 C. 24m2 D. 24 3m2
二、填空题(本大题共8小题,共24.0分)
11. 为了调查某品牌护眼灯的使用寿命,比较适合的调查方式是______ (填“普查”或“抽样调查”).
12. 一个圆锥的底面半径为5,高为12,则它的体积为______ .
13. 在综合与实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动.有一张矩形纸片ABCD如图所示,点N在边AD上,现将矩形折叠,折痕为BN,点A对应的点记为点M,若点M恰好落在边DC上,则图中与△NDM一定相似的三角形是______ .
14. 若x满足(x−2)x+1=1,则整数x的值为______ .
15. 新高考“3+1+2”选科模式是指,除语文、数学、外语3门科目以外,学生应在历史和物理2门首选科目中选择1科,在思想政治、地理、化学、生物学4门再选科目中选择2科.某同学从4门再选科目中随机选择2科,恰好选择地理和化学的概率为______ .
16. 若关于x的不等式组3(x−1)>x−68−2x+2a≥0有三个整数解,则实数a的取值范围为______ .
17. 1261年,我国宋朝数学家杨辉在其著作《详解九章算法》中提到了如图所示的数表,人们将这个数表称为“杨辉三角”.
观察“杨辉三角”与右侧的等式图,根据图中各式的规律,(a+b)7展开的多项式中各项系数之和为______ .
18. 如图,在△ABC中,将AB绕点A顺时针旋转α至AB′,将AC绕点A逆时针旋转β至AC′(0°<α<180°,0°<β<180°),得到△AB′C′,使∠BAC+∠B′AC′=180°,我们称△AB′C′是△ABC的“旋补三角形“,△AB′C′的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.下列结论正确的有______ .
①△ABC与△AB′C′面积相同;
②BC=2AD;
③若AB=AC,连接BB′和CC′,则∠B′BC+∠CC′B′=180°;
④若AB=AC,AB=4,BC=6,则B′C′=10.
三、解答题(本大题共10小题,共66.0分。解答应写出文字说明,证明过程或演算步骤)
19. (本小题4.0分)
计算:|1− 2|−2cos45°+(12)−1.
20. (本小题4.0分)
先化简,再求值:2xx+2−xx−2+4xx2−4,其中x=1.
21. (本小题5.0分)
为营造良好体育运动氛围,某学校用800元购买了一批足球,又用1560元加购了第二批足球,且所购数量是第一批购买数量的2倍,但单价降了2元,请问该学校两批共购买了多少个足球?
22. (本小题6.0分)
某风景区观景缆车路线如图所示,缆车从点A出发,途经点B后到达山顶P,其中AB=400米,BP=200米,且AB段的运行路线与水平方向的夹角为15°,BP段的运行路线与水平方向的夹角为30°,求垂直高度PC.(结果精确到1米,参考数据:sin15°≈0.259,cos15°≈0.966,tan15°≈0.268)
23. (本小题7.0分)
为了解我校学生本学期参加志愿服务的情况,随机调查了我校的部分学生,根据调查结果,绘制出如图统计图.若我校共有1000名学生,请根据相关信息,解答下列问题:
(1)本次接受调查的学生人数为______ ,扇形统计图中的m= ______ ;
(2)求所调查的学生本学期参加志愿服务次数的平均数;
(3)学校为本学期参加志愿服务不少于7次的学生颁发“志愿者勋章”,请估计我校获“志愿者勋章”的学生人数.
24. (本小题7.0分)
如图,在平行四边形ABCD中,E为线段CD的中点,连接AC,AE,延长AE,BC交于点F,连接DF,∠ACF=90°.
(1)求证:四边形ACFD是矩形;
(2)若CD=13,CF=5,求四边形ABCE的面积.
25. (本小题7.0分)
一次函数y=−x+m与反比例函数y=kx的图象交于A,B两点,点A的坐标为(1,2).
(1)求一次函数和反比例函数的表达式;
(2)求△OAB的面积;
(3)过动点T(t,0)作x轴的垂线l,l与一次函数y=−x+m和反比例函数y=kx的图象分别交于M,N两点,当M在N的上方时,请直接写出t的取值范围.
26. (本小题8.0分)
某建筑物的窗户如图所示,上半部分△ABC是等腰三角形,AB=AC,AF:BF=3:4,点G、H、F分别是边AB、AC、BC的中点;下半部分四边形BCDE是矩形,BE//IJ//MN//CD,制造窗户框的材料总长为16米(图中所有黑线的长度和),设BF=x米,BE=y米.
(1)求y与x之间的函数关系式,并求出自变量x的取值范围;
(2)当x为多少时,窗户透过的光线最多(窗户的面积最大),并计算窗户的最大面积.
27. (本小题9.0分)
如图,AB是⊙O的直径,点C是圆上的一点,CD⊥AD于点D,AD交⊙O于点F,连接AC,若AC平分∠DAB,过点F作FG⊥AB于点G,交AC于点H,延长AB,DC交于点E.
(1)求证:CD是⊙O的切线;
(2)求证:AF⋅AC=AE⋅AH;
(3)若sin∠DEA=45,求AHFH的值.
28. (本小题9.0分)
如图,二次函数y=ax2+bx+c的图象与x轴交于A,B两点,且自变量x的部分取值与对应函数值y如下表:
x
…
−1
0
1
2
3
4
…
y
…
0
−3
−4
−3
0
5
…
(1)求二次函数y=ax2+bx+c的表达式;
(2)若将线段AB向下平移,得到的线段与二次函数y=ax2+bx+c的图象交于P,Q两点(P在Q左边),R为二次函数y=ax2+bx+c的图象上的一点,当点Q的横坐标为m,点R的横坐标为m+ 2时,求tan∠RPQ的值;
(3)若将线段AB先向上平移3个单位长度,再向右平移1个单位长度,得到的线段与二次函数y=1t(ax2+bx+c)的图象只有一个交点,其中t为常数,请直接写出t的取值范围.
答案和解析
1.【答案】B
【解析】解:由题意得,
实数2023的相反数是−2023,
故选:B.
运用知识点:实数a的相反数是−a进行求解.
此题考查了实数相反数的求解能力,关键是能准确理解并运用相反数的定义进行求解.
2.【答案】C
【解析】解:选项A、B、D都不能找到一个点,使图形绕某一点旋转180°后与原来的图形重合,所以不是中心对称图形.
选项C能找到一个点,使图形绕某一点旋转180°后与原来的图形重合,所以是中心对称图形.
故选:C.
根据中心对称图形的概念判断.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形
本题考查的是中心对称图形,中心对称图形是要寻找对称中心,旋转180度后与自身重合.
3.【答案】A
【解析】解:1268000000=1.268×109.
故选:A.
将一个数表示成a×10n的形式,其中1≤|a|<10,n为整数,这种记数方法叫做科学记数法,据此即可得出答案.
本题考查科学记数法—表示较大的数,科学记数法是基础且重要知识点,必须熟练掌握.
4.【答案】A
【解析】解:从上面看,是一个矩形.
故选:A.
找到从上面看所得到的图形即可,注意看见的棱用实线表示.
本题考查了三视图的知识,俯视图是从物体的上面看得到的视图.
5.【答案】D
【解析】解:∵a+b>0,ab>0,
∴以a>0,b>0,
A、(a,b)在第一象限,因为小手盖住的点在第四象限,故此选项不符合题意;
B、(−a,b)在第二象限,因为小手盖住的点在第四象限,故此选项不符合题意;
C、(−a,−b)在第三象限,因为小手盖住的点在第四象限,故此选项不符合题意;
D、(a,−b)在第四象限,因为小手盖住的点在第四象限,故此选项符合题意.
故选:D.
因为ab>0,所以a、b同号,又a+b>0,所以a>0,b>0,观察图形判断出小手盖住的点在第四象限,然后解答即可.
本题考查了点的坐标,记住各象限内点的坐标的符号是解题的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(−,+);第三象限(−,−);第四象限(+,−).
6.【答案】B
【解析】解:该同学五项评价得分从小到大排列分别为7,8,9,9,10,
出现次数最多的数是9,所以众数为9,
位于中间位置的数是8,所以中位数是9,
平均数为15×(7+8+9+9+10)=8.6
故选:B.
利用众数、中位数及平均数的定义写出答案即可.
本题考查了统计的知识,掌握众数、中位数及平均数的定义是关键.
7.【答案】C
【解析】解:A、一个函数是一次函数不一定是正比例函数,故本选项不符合题意;
B、有两组对角相等的四边形一定是平行四边形,故本选项不符合题意;
C、两条直角边对应相等的两个直角三角形一定全等,故本选项符合题意;
D、一组数据的方差不一定大于这组数据的标准差,故本选项不符合题意;
故选:C.
根据正比例函数的定义、平行四边形的判定、直角三角形全等的判定、标准差的概念对各选项进行判断,选出正确答案即可.
本题考查了正比例函数的定义、平行四边形的判定、直角三角形全等的判定、标准差的概念等知识点,属于基础题,解答本题的关键是熟练掌握各知识点的概念.
8.【答案】A
【解析】解:设成本为m,标价为(1+25%)m,
设降价幅度为x,
∴粽子降价出售的售价为:(1+25%)m(1−x),
为了不亏本,即售价大于等于成本,
(1+25%)m(1−x)≥m,
解得x≤20%,
故选:A.
设降价幅度为x,降价后的价格大于等于成本列式.
本题考查销售问题,解题的关键是商品的售价表示方法与成本间的比较.
9.【答案】D
【解析】解:∵四边形ABCD和四边形BGHF是完全相同的菱形,
∴∠DBE=∠BAD=α,AB=AD,∠ABD=∠CBD=∠CBE+∠DBE=β+α,
∴∠ADB=∠ABD=β+α,
∵∠BAD+∠ADB+∠ABD=180°,
∴α+β+α+β+α=180°,
∴β=90°−32α,
故选:D.
由菱形的性质得∠DBE=∠BAD=α,AB=AD,∠ABD=∠CBD=β+α,再由等腰三角形的性质得∠ADB=∠ABD=β+α,然后由三角形内角和定理即可得出结论.
本题考查了菱形的性质、等腰三角形的性质、三角形内角和定理得知识,熟练掌握菱形的性质是解题的关键.
10.【答案】C
【解析】解:由题意可知:AB:BC=1: 3,设AB=a,则BC= 3a,
如图,过点P作PE垂直于CB的延长线于点E,
∵PA=t,则PB=a−t,BQ= 3t,
在Rt△PBE中,∠PBE=180°−∠ABC=60°,
∴PE= 32(a−t),
则y=12× 3t× 32(a−t),化简得:y=−34t2+34at.
由二次函数图象可知,函数的顶点纵坐标为3,
∴0−(34a)24×(−34)=316a2=3,
∴a2=16,
∵a为正数,
∴a=4,
∴AB=4,则BC=4 3,
如图,过点A作AF垂直于CB的延长线于点F,
在Rt△ABF中,∠ABF=60°,
∴AF= 32×4=2 3,
∴S▱ABCD=BC×AF=2 3×4 3=24m2.
故答案为:C.
首先根据题意知道AB:BC=1: 3,设AB=a,则BC= 3a,从而可用a和t表示出△PBQ的面积,即为图2中二次函数的关系式;再根据图象可知顶点纵坐标为3,根据顶点公式可求出a的值,从而得到了AB和BC的值;最后再根据∠ABC=120°这一条件,求出平行四边形的高,从而得到面积.
本题属于运动综合题,将动点问题的函数图象与解三角形、图形面积结合起来考查.解题的关键是审清题意,找出平行四边形两邻边的关系,并通过设参数的形式列出动点的函数关系式,并对照函数图象上已知的顶点纵坐标求出平行四边形的边长,从而求出平行四边形面积.
11.【答案】抽样调查
【解析】解:调查某品牌护眼灯的使用寿命,具有破坏性,适合采用的调查方式是抽样调查.
故答案为:抽样调查.
根据全面调查与抽样调查的特点解答即可.
本题考查全面调查与抽样调查,理解全面调查与抽样调查的意义是正确判断的关键.
12.【答案】100π
【解析】解:底面半径为5,高为12的圆锥的体积=13×52π×12=100π,
故答案为:100π.
根据圆锥的体积公式即可得到结论.
本题考查了圆锥的体积的计算,熟练掌握圆锥的体积公式是解题的关键.
13.【答案】△MCB
【解析】解:∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°,
∴∠DNM+∠DMN=90°,由折叠的性质可知,∠BMN=∠A=90°,
∴∠DMN+∠CBM=90°,
∴∠DNM=∠CMB,
∴△NDM∽△MCB,
故答案为:△MCB.
利用矩形的性质得到∠D=∠C=90°,然后利用折叠的性质推导出∠BMN=∠A=90°,进而得到∠DNM=∠CMB,由此推断出△NDM∽△MCB.
本题主要考查了相似三角形的判定、矩形的性质以及翻折变换(折叠问题),熟练掌握相似三角形的判定方法是解答本题的关键:两角法:有两组角对应相等的两个三角形相似.
14.【答案】−1或3或1
【解析】解:由题意得:
①x+1=0,
解得:x=−1;
②x−2=1,
解得:x=3;
③x−2=−1,x+1为偶数,
解得:x=1,
故答案为:−1或3或1.
根据零指数幂可得x+1=0,根据有理数的乘方可得x−2=1;x−2=−1,x+1为偶数,再解即可.
此题主要考查了零指数幂,以及有理数的乘方,关键是注意要分类讨论,不要漏解.
15.【答案】16
【解析】解:画树状图如图所示,
由图可知,共有12种等可能结果,其中该同学恰好选中地理和化学两科的有2种结果,
所以该同学恰好选中化学、生物两科的概率为212=16.
故答案为:16.
画树状图得出所有等可能结果,从中找到恰好选中地理和化学两科的结果数,再利用概率公式计算可得.
本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式求事件A或B的概率.
16.【答案】−3≤a<−2
【解析】解:解不等式3(x−1)>x−6,得:x>−1.5,
解不等式8−2x+2a≥0,得:x≤a+4,
∵不等式组有三个整数解,
∴不等式组的整数解为−1,0、1,
则1≤a+4<2,
解得−3≤a<−2.
故答案为:−3≤a<−2.
首先解不等式组求得解集,然后根据不等式组有三个整数解,确定整数解,则可以得到一个关于a的不等式组求得a的范围.
本题考查不等式组的解法及整数解的确定.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.
17.【答案】128
【解析】解:∵(a+b)0=1,系数之和是20=1;
(a+b)1=a+b,系数之和是21=2;
(a+b)2=a2+2ab+b2,系数之和是22;
……
(a+b)n,展开各项系数之和是2n.
∴(a+b)7展开各项的系数之和为27=128.
故答案为:128.
根据图示可得出一般规律,利用规律计算即可.
本题考查了完全平方公式的延伸应用,属于规律性探究题型,从特殊到一般规律的推出是数学探究的常用方法.
18.【答案】①②③
【解析】证明:延长AD至E,使DE=AD,连接B′E,C′E,
∵AD是中线,
∴B′D=C′D,
∴四边形AC′EB′是平行四边形,
∴B′E//AC′,B′E=AC′,S△B′C′A=12S▱B′EC′A=S△AB′E,
∴∠B′AC′+∠AB′E=180°,
∵∠BAC+∠B′AC′=180°,
∴∠BAC=∠AB′E,
∵将AB绕点A顺时针旋转α至AB′,将AC绕点A逆时针旋转β至AC′,
∴AB=AB′,AC=AC′=B′E,
在△BAC和△AB′E中,
BA=AB′∠BAC=∠AB′ECA=B′E,
∴△BAC≌△AB′E(SAS),
∴BC=AE,S△ABC=S△AB′E,
∴S△ABC=S△B′C′A,故①正确;
∵AE=2AD,
∴BC=2AD,故②正确;
∵AB=AC,
∴AB′=AC′=AB=AC,
∴∠ABC=∠ACB,∠ABB′=∠AB′B,∠ACC′=∠AC′C,∠AB′C′=∠AC′B′,
∵∠BAC+∠B′AC′=180°,
∴α+β=180°,∠B′C′A+∠ABC=90°,
∴∠ABB′+∠AC′C=90°,
∴∠B′BC+∠CC′B′=180°;故③正确;
∵BC=6,
∴AD=3,
∵AB′=AC′=AB=AC=4,
∴平行四边形AC′EB′是菱形,
∴B′C′⊥AE,B′D=C′D,
∴B′D= B′A2−AD2= 16−9= 7,
∴B′C′=2 7,故④错误,
故答案为:①②③.
由“SAS”可证△BAC≌△AB′E,可得BC=AE,S△ABC=S△AB′E,可求S△ABC=S△B′C′A,BC=2AD,故①②正确;由等腰三角形的性质和三角形内角和定理可求∠B′BC+∠CC′B′=180°;故③正确;通过证明平行四边形AC′EB′是菱形,可得B′C′⊥AE,B′D=C′D,由勾股定理可求B′C′的长,即可判断④,即可求解.
本题是三角形综合题,考查了全等三角形的判定和性质,等腰三角形的性质,勾股定理,平行四边形的判定和性质,菱形的判定和性质,灵活运用这些性质解决问题是解题的关键.
19.【答案】解:|1− 2|−2cos45°+(12)−1
= 2−1−2× 22+2
= 2−1− 2+2
=1.
【解析】先化简各式,然后再进行计算即可解答.
本题考查了实数的运算,负整数指数幂,特殊角的三角函数值,准确熟练地化简各式是解题是关键.
20.【答案】解:原式=2x(x−2)(x+2)(x−2)−x(x+2)(x+2)(x−2)+4x(x+2)(x−2)
=2x2−4x−x2−2x+4x(x+2)(x−2)
=x2−2x(x+2)(x−2)
=x(x−2)(x+2)(x−2)
=xx+2,
当x=1时,原式=11+2=13.
【解析】先通分,再计算加减,再把x的值代入进行计算即可.
本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.
21.【答案】解:设第一批足球单价为x元,则第二批足球的单价为(x−2)元,
由题意得:800x×2=1560x−2,
解得:x=80,
经检验,x=80是原方程的解,且符合题意,
则x−2=78,
80080+156078=30,
答:该学校两批共购买了30个足球.
【解析】设第一批足球单价为x元,则第二批足球的单价为(x−2)元,根据学校用800元购买了一批足球,又用1560元加购了第二批足球,且所购数量是第一批购买数量的2倍列方程即可得结论.
本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
22.【答案】解:过点B作BD⊥PC,垂足为D,过点B作BE⊥AC,垂足为E,
由题意得:CD=BE,
在Rt△ABE中,∠A=15°,AB=400米,
∴BE=AB⋅sin15°≈400×0.259=103.6(米),
∴CD=BE=103.6米,
在Rt△BDP中,∠PBD=30°,BP=200米,
∴DP=12BP=100(米),
∴PC=PD+DC≈204(米),
∴垂直高度PC约为204米.
【解析】过点B作BD⊥PC,垂足为D,过点B作BE⊥AC,垂足为E,根据题意可得:CD=BE,然后分别在Rt△ABE和Rt△BDP中,利用锐角三角函数的定义求出BE和DP的长,从而利用线段的和差关系进行计算,即可解答.
本题考查了解直角三角形的应用−坡度坡角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
23.【答案】40 25
【解析】解:(1)4÷10%=40(人),
10÷40×100%=25%,即m=25,
故答案为:40,25;
(2)5×4+6×8+7×15+8×10+9×340=7(次),
故所调查的学生本学期参加志愿服务次数的平均数为7次;
(3)1000×(37.5+25%+7.5%)=700(名),
答:估计我校获“志愿者勋章”的学生人数大约有700名.
(1)由两个统计图可得样本参加志愿服务为5次的有4人,占调查人数的10%,由频率可求出调查人数,进而求出参加志愿服务为8次所占的百分比,得出m的值;
(2)根据加权平均数公式进行计算即可;
(3)用样本中的“参加志愿服务7次”的学生所占的百分比去估计全校1000名学生“参加志愿服务7次”所占的百分比,再根据频率进行计算即可.
本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
24.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠ADE=∠FCE,∠DAE=∠CFE,
∵E为线段CD的中点,
∴DE=CE,
∴△ADE≌△FCE(AAS),
∴AE=FE,
∴四边形ACFD是平行四边形,
∵∠ACF=90°,
∴四边形ACFD是矩形;
(2)解:∵CD=13,CF=5,
∴BC=CF=5,
∵四边形ACFD是矩形,
∴∠CFD=90°,AC=DF,
∴DF= CD2−CF2= 132−52=12,
∵△ADE≌△FCE,
∴四边形ABCE的面积=平行四边形ABCD=BF⋅AC=10×12=120.
【解析】(1)证明△ADE≌△FCE(AAS),得AE=FE,所以四边形ACFD是平行四边形,再根据有一个角是直角的平行四边形是矩形即可解决问题;
(2)根据矩形的性质和勾股定理求出DF的值,由△ADE≌△FCE,可得四边形ABCE的面积=平行四边形ABCD,进而可以解决问题.
本题考查了矩形的判定与性质,平行四边形的判定与性质,全等三角形的判定与性质,解决本题的关键是掌握矩形的性质.
25.【答案】解:(1)∵一次函数y=−x+m与反比例函数y=kx的图象交于A,B两点,点A的坐标为(1,2),
∴2=−1+m,2=k1,
∴m=3,k=2,
∴一次函数表达式为y=−x+3,反比例函数的表达式为y=2x;
(2)由y=−x+3y=2x,解得x=1y=2或x=2y=1,
∴B(2,1),
设一次函数y=−x+3与x轴的交点为C,则C(3,0),
∴S△AOB=S△AOC−S△BOC=12×3×2−12×3×1=32;
(3)观察图象,当M在N的上方时,t的取值范围是t<0或1
(2)解析式联立,解方程组求得点B的坐标,利用S△AOB=S△AOC−S△BOC求得即可;
(3)根据图象即可求得.
本题是反比例函数与一次函数的交点问题,考查了待定系数法求函数的解析式,三角形的面积,数形结合是解题的关键.
26.【答案】解:(1)∵△ABC是等腰三角形,F是BC的中点,
∴BF=CF,AF⊥BC,AB=AC,
∵BF=x米,
∴CF=x米,BC=2BF=2x米,
∵AF:BF=3:4,
∴AF=34x米,
在Rt△AFB中,由勾股定理得AB= AF2+BF2= (34x)2+x2=54x米,
∴AC=AB=54x米,
∵点G、H分别是边AB、AC的中点,∠AFB=∠AFC=90°,
∴FG=12AB=58x米,FH=12AC=58x米,
∵四边形BCDE是矩形,
∴ED=BC=2x米,BE=CD=y米,
∵BE//IJ//MN//CD,
∴BE=IJ=MN=CD=y米,
∵制造窗户框的材料总长为16米,
∴AB+AC+FG+FH+AF+BC+ED+BE+IJ+MN+CD=16米,
∴54x+54x+58x+58x+34x+2x+2x+4y=16,
整理得y=−178x+4;
由题意得x>0−178x+4>0,
解得0
设窗户的面积为W平方米,
则W=S△ABC+S矩形BCDE
=34x2−174x2+8x
=−72x2+8x
=−72(x−87)2+327,
∵−72<0,
∴W有最大值,
当x=87米时,W最大,最大值为327平方米.
【解析】(1)根据等腰三角形的性质求出CF的长,即可求出BC的长,根据AF:BF=3:4即可求出AF的长,再根据勾股定理求出AB的长,AC的长,再根据直角三角形斜边上的中线等于斜边的一半求出FG、FH的长,根据矩形的性质求出ED=BC=2x米,BE=IJ=MN=CD=y米,最后根据制造窗户框的材料总长为16米列出方程即可得到y与x之间的函数关系式;
(2)根据窗户的面积等于△ABC的面积加上矩形BCDE的面积计算,再根据配方法求二次函数的顶点坐标即可.
本题考查了等腰三角形的性质,矩形的性质,二次函数的应用,根据材料总长用含x的式子表示y,从而运用函数性质求最大值是解题的关键.
27.【答案】(1)证明:连接OC,
∵AC平分∠DAB,
∴∠DAC=∠EAC,
∵∠OCA=∠EAC,
∴∠DAC=∠OCA,
∴OC//AD,
∵CD⊥AD,
∴OC⊥AD,
∵OC是半径,
∴CD是⊙O的切线;
(2)证明:∵AC平分∠DAB,
∴∠DAC=∠EAC,
又∵CD⊥AD,FG⊥AB,
∴∠AGF=∠D=90°,
∴∠AFG+∠DAG=90°,∠E+∠DAE=90°,
∴∠AFG=∠DEA,
∴△AHF∽△ACE,
∴AHAC=AFAE,
即AF⋅AC=AE⋅AH;
(3)过H作HM⊥AD,如图:
由(2)知∠AFG=∠DEA,
∴sin∠DEA=45=sin∠ADG=AGAD,
设AG=5x,AD=4x,则DG=3x,
∵AC平分∠DAB,
∴MH=GH,AG=AM=3x,
∴MF=x,
设GH=MH=a,
∴tan∠AFG=AGGF=MHMF,
∴4x3x=ax,
∴a=43x,
∴FH=3x−43x=83x,
AH= AG2+GH2= (4x)2+(43x)2=4 103x,
∴AHFH=4 103x83x= 102.
【解析】(1)连接OC,证明OC//AD即可得证;
(2)证明△AHF∽△ACE即可得证;
(3)过H作HM⊥AD,由∠DEA=∠ADG可得sin∠DEA=45=sin∠ADG,设AG=5x,AD=4x,则DG=3x,AM=3x,MF=x,由角平分线的性质可得MH=GH,设GH=MH=a,则MF=再说明△MHF∽△GAF,从而得出对边成比例即可表示出a=43x,从而可表示出FH,再由勾股定理表示出AH即可解答.
本题考查了切线的判定,相似三角形的判定和性质,锐角三角函数,正确作出辅助线是解题关键.
28.【答案】解:(1)∵二次函数y=ax2+bx+c的图象经过A(−1,0),B(3,0),(0,−3)三个点,
∴a−b+c=09a+3b+c=0c=−3,
∴a=1b=−2c=−3,
∴二次函数的表达式为:y=x2−2x−3.
(2)过R作RT⊥PQ,垂足为T,
∵点Q的横坐标为m,点R的横坐标为m+ 2,
∴QT= 2,
∵二次函数y=x2−2x−3的对称轴为直线x=1,
∴点P,Q关于直线x=1对称,
∵Q到x=1的距离是m−1,
∴PQ=2(m−1)=2m−2,
∴PT=2m−2+ 2,
∵yR=(m+ 2)2−2(m+ 2)−3,yT=yQ=m2−2m−3,
∴RT=yR−yT=2 2m−2 2+2,
∴在Rt△RPT中,tan∠RPQ=RTPT=2 2 m−2 2+22m−2+ 2= 2.
(3)线段AB先向上平移3个单位长度,再向右平移1个单位长度,得到的线段设为A′B′,则A′(0,3),B′(4,3),
二次函数y=1t(x2−2x−3)与x轴交于A(−1,0),B(3,0)两点,对称轴为直线x=1,二次函数y=1t(x2−2x−3)与二次函数y=(x2−2x−3)只是开口大小和方向发生了变化,并且|1t|越大,开口越小.若线段A′B′与二次函数y=1t(x2−2x−3)的图象只有一个交点,分以下三种情况:
①当t>0时,开口向上,如图,线段A′B′与二次函数y=1t(x2−2x−3)的图象只有一个交点,当抛物线经过B′(4,3)时开口最大,1t最小,t最大,把(4,3)代入y=1t(x2−2x−3)得t=53,
∴0
②当t<0时,开口向下,如图,线段A′B′与二次函数y=1t(x2−2x−3)的图象只有一个交点(1,3),代入y=1t(x2−2x−3)得t=−43.
③当t<0时,开口向下,如图,线段A′B′与二次函数y=1t(x2−2x−3)的图象只有一个交点,当抛物线经过A′(0,3)时开口最大,|1t|最小,t最小,把(0,3)代入y=1t(x2−2x−3)得t=−1,
∴−1
综上,t的取值范围是:t=−43或−1
(2)构造直角三角形,把∠RPQ放在直角三角形中,用m表示tan∠RPQ的值并化简;
(3)二次函数y=1t(x2−2x−3)与x轴交于A(−1,0),B(3,0)两点,对称轴为直线x=1,二次函数y=1t(x2−2x−3)与二次函数y=(x2−2x−3)只是开口大小和方向发生了变化,并且|1t|越大,开口越小,所以利用数形结合寻求线段与抛物线的交点问题.
本题考查了用待定系数法求二次函数表达式,解直角三角形,渗透了分类和数形结合的思想,对于第(3)问,关键是研究二次函数y=1t(x2−2x−3)的性质,找到分类标准.
2020年黑龙江省大庆市中考数学试卷: 这是一份2020年黑龙江省大庆市中考数学试卷,共29页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022届黑龙江省大庆市肇源县中考联考数学试卷含解析: 这是一份2022届黑龙江省大庆市肇源县中考联考数学试卷含解析,共19页。试卷主要包含了下列哪一个是假命题等内容,欢迎下载使用。
2022年黑龙江省大庆市中考数学试卷解析版: 这是一份2022年黑龙江省大庆市中考数学试卷解析版,共46页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












