

2022-2023学年湖北省武汉外国语学校高二(下)期末数学试卷(含解析)
展开2022-2023学年湖北省武汉外国语学校高二(下)期末数学试卷
1. (1−2x)8展开式中第4项的二项式系数为( )
A. −448 B. 1120 C. 56 D. 70
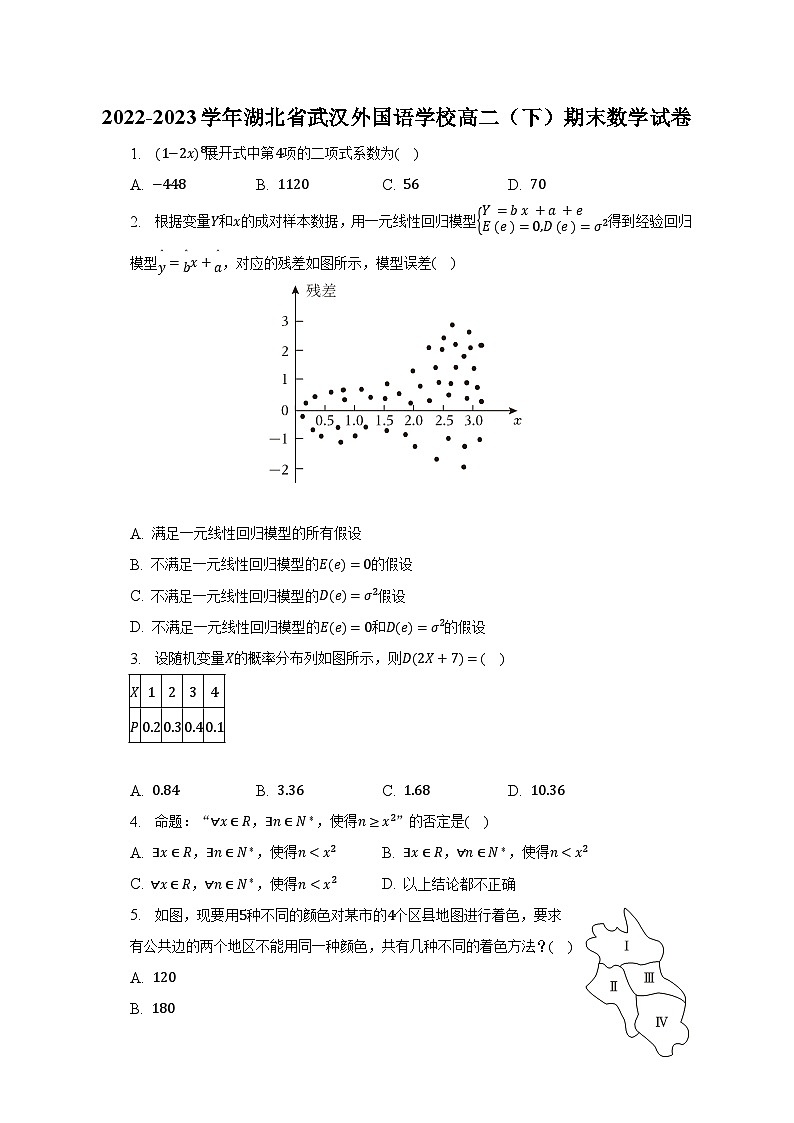
2. 根据变量Y和x的成对样本数据,用一元线性回归模型Y=bx+a+eE(e)=0,D(e)=σ2得到经验回归模型y =b x+a ,对应的残差如图所示,模型误差( )
A. 满足一元线性回归模型的所有假设
B. 不满足一元线性回归模型的E(e)=0的假设
C. 不满足一元线性回归模型的D(e)=σ2假设
D. 不满足一元线性回归模型的E(e)=0和D(e)=σ2的假设
3. 设随机变量X的概率分布列如图所示,则D(2X+7)=( )
X
1
2
3
4
P
0.2
0.3
0.4
0.1
A. 0.84 B. 3.36 C. 1.68 D. 10.36
4. 命题:“∀x∈R,∃n∈N*,使得n≥x2”的否定是( )
A. ∃x∈R,∃n∈N*,使得n
A. 120
B. 180
C. 221
D. 300
6. 设随机变量X~N(0,1),则X的密度函数为( )
A. f(x)=1 2πe−x22 B. f(x)=1 2πe−(x−1)22
C. f(x)=1 2πe−x22 D. f(x)=1 2πe−(x−1)22
7. 设随机变量X~B(n,p),记pk=Cnkpk(1−p)n−k,k=0,1,2,…,n,下列说法正确的是( )
A. 当k由0增大到n时,pk先增后减,在某一个(或两个)k值处达到最大.二项分布当p=0.5时是对称的,当p<0.5时向右偏倚,当p>0.5时向左偏倚
B. 如果(n+1)p为正整数,当且仅当k=(n+1)p时,pk取最大值
C. 如果(n+1)p为非整数,当且仅当k取(n+1)p的整数部分时,pk取最大值
D. E(X)=np(1−p)
8. 已知函数f(x)=x2+x−1ex,则方程f(f(x))=−1的根的个数是( )
A. 2 B. 4 C. 5 D. 6
9. 设离散型随机变量X,非零常数a,b,下列说法正确的有( )
A. E(aX+b)=aE(X+ba) B. D(aX+b)=a2D(X+ba)
C. D(X)=E(X2)−E(X) D. D(X)=E(X2)−(E(X))2
10. 下列说法正确的有( )
A. 命题:“∀x∈R,1x>0”的否定是:“∃x∈R,1x≤0”
B. 命题:“若x>1,则2x+1>5”的否定是:“若x>1,则2x+1≤5”
C. 已知x,y∈R,则“x或y为有理数”是“xy为有理数”的既不充分也不必要条件
D. 如果x,y是实数,则“x≠y”是“cosx≠cosy”的必要不充分条件
11. 已知定义在(0,+∞)上的函数f(x)满足:对∀x,y∈(0,+∞),都有f(xy)=f(x)+f(y),则对于∀x,y∈(0,+∞),n∈N*,下式成立的有( )
A. f(x+y)=f(x)f(y) B. f(xy)=f(x)−f(y)
C. f(xn)=nf(x) D. f(nx)=1nf(x)
12. 下列不等式中成立的有( )
A. log43>log65
B. 当x>0时,x(ex−1+2)>x2+2lnx+2
C. 当x>−m,且m≤2时,ex>ln(x+m)
D. x∈R时,sinx≤x
13. 函数f(x)=ex(2x−1)x−1的单调减区间为______ .
14. 2160有______ 个不同的正因数.
15. 已知某商品进价为a元/件,根据以往经验,当售价是b(b≥43a)元/件时,可卖出c件,市场调查表明,当售价下降10%时,销量可增加40%.现决定一次性降价,为获得最大利润,售价应定为______ 元/件.(用含a,b的式子表示)
16. 已知n∈N*,n≥2,计算Cn1+22Cn2+32Cn3+…+n2Cnn= ______ .
17. 如图,△ABC和△DBC所在平面垂直,且AB=BC=BD,∠CBA=∠DBC=120°,求:
(1)直线AD与平面BDC所成角的大小;
(2)平面ABD和平面BDC夹角的余弦值.
18. (1)设集合A={x|x2−(a+1)x+a=0,a∈R},B={x|x2−5x+4=0},求:A∩B,A∪B.
(2)已知x,y,z都是正数,且满足x32+y32+z32=32,求证:xy+z+yz+x+zx+y≤34 xyz.
19. 已知数列{an}是等比数列,其前n项和为Sn,若a3=32,S3=92.
(1)求数列{an}的通项公式;
(2)已知数列{bn}是等差数列,b1=2,如果等差数列{cn}的通项cn满足cn=n2bn(n∈N+).令xn=an⋅bncn(n∈N+),求数列{xn}的前n项和Tn.
20. 甲、乙、丙三人相互做传球训练,第1次由甲将球传出,每次传球时,传球者都等可能地将球传给另外两个人中的任何一人.
(1)求n(n∈N+)次传球后球在甲手中的概率;
(2)求n(n∈N+)次传球后球在乙手中的概率;
(3)已知:若随机变量Xi服从两点分布,且P(Xi=1)=1−P(Xi=0)=qi,i=1,2,…,n,则E(i=1nXi)=i=1nqi,记前n次传球后(即从第1次传球到第n次传球后)球在甲手中的次数为Y,求E(Y).
21. 平面内与两定点A1(−a,0),A2(a,0)(a>0)连线的斜率之积等于非零常数m的点的轨迹,加上A1,A2两点所成的曲线记为曲线C.
(1)求曲线C的方程,并讨论C的形状与m值的关系;
(2)若m=−1时,对应的曲线为C1;对给定的m∈(−1,0)∪(0,+∞),对应的曲线为C2.设F1,F2是C2的两个焦点,试问:在C1上是否存在点N,使得△F1NF2的面积S=|m|a2,并证明你的结论.
22. 已知矩形ABCD(AB>AD)的周长为6.
(1)把△ABC沿AC向△ADC折叠,AB折过去后交DC于点P,求△ADP的最大面积;
(2)若AB=2,AD=1,如图,AB,AD分别在x轴,y轴的正半轴上,A点与坐标原点重合,将矩形ABCD折叠,使A点落在线段DC上,设折痕所在直线的斜率为k,问当k为何值时,折痕的长度取最大值.
答案和解析
1.【答案】C
【解析】解:根据二项式系数的定义可知,二项式各项二项式系数为:C80,C81,C82,C83,…C88,
所以(1−2x)8的展开式中第4项的二项式系数是C83=56.
故选:C.
根据已知条件,结合二项式系数的定义,即可求解.
本题考查二项展开式中二项式系数的计算,注意二项展开式项的系数与二项式系数的区别,是基础题,
2.【答案】C
【解析】解:用一元线性回归模型Y=bx+a+eE(e)=0,D(e)=σ2得到经验回归模型y =b x+a ,
根据对应的残差图,残差的均值E(e)=0可能成立,
但明显残差的x轴上方的数据更分散,D(e)=σ2不满足一元线性回归模型,正确的只有C.
故选:C.
根据一元线性回归模型Y=bx+a+eE(e)=0,D(e)=σ2有关概念即可判断.
本题考查了一元线性回归模型的含义,属于中档题.
3.【答案】B
【解析】解:由题意知:E(X)=1×0.2+2×0.3+3×0.4+4×0.1=2.4.
所D(X)=(1−24)2×0.2+(2−0.4)2×0.3+(3−0.4)2×0.4+(4−0.4)2×0.1=0.84,
D(2X+7)=4D(X)=4×0.84=3.36.
故选:B.
先计算出E(X),即可计算出D(X),即可计算D(2X+7).
本题考查排列组合的应用,属于中档题.
4.【答案】B
【解析】解:命题命题“∀x∈R,∃n∈N*,使得n⩾x2”,
则命题的否定为:∃x∈R,∀n∈N*,使得n
根据含有量词的命题的否定即可得到结论.
本题主要考查含有量词的命题的否定,比较基础.
5.【答案】B
【解析】解:先排I,Ⅱ,Ⅲ共有A53=60种,Ⅳ有C31=3种,
故不同的着色方法数有60×3=180种.
故选:B.
先排I,Ⅱ,Ⅲ最后排Ⅳ,由此求得不同着色方法数.
本题考查排列组合的应用,属于基础题.
6.【答案】A
【解析】解:随机变量X~N(0,1),
所以μ=0,σ=1,
则X的密度函数为f(x)=1 2πe−x22.
故选:A.
根据X的密度函数,代入即可求得答案.
本题考查正态分布,属于基础题.
7.【答案】C
【解析】解:根据题意,依次分析选项:
对于A,二项分布当p=0.5时是对称的,当p>0.5时向右偏倚,当p<0.5时向左偏倚,A错误;
对于B,如果(n+1)p为正整数,当k=(n+1)p或k=(n+1)p−1时,pk取最大值,B错误;
对于C,如果(n+1)p为非整数,当且仅当k取(n+1)p的整数部分时,pk取最大值,C正确;
对于D,E(X)=np,D错误.
故选:C.
根据题意,由二项分步的性质依次分析选项,即可得答案.
本题考查二项分布的性质,涉及其概率最大值的性质,属于基础题.
8.【答案】B
【解析】解:f′(x)=−x2+x+2ex=−(x−2)(x+1)ex,
可得f(x)在(−∞,−1)递减,在(−1,2)递增,在(2,+∞)递减,
且f(x)=0时,x=−1± 52,f(−1)=−e,
f(x)的草图如下:
根据图象可得方程f(t)=−1有两个实根t1,t2,且t1=0,t2∈(−1− 52,−1),
又方程f(x)=0有两个根,f(x)=t2有两个根,
所以方程f(f(x))=−1的根的个数是4.
故选:B.
利用导数求得函数f(x)的单调性,画出f(x)的图象,分别求得方程f(t)=−1,f(x)=t的根即可.
本题考查了函数的零点与方程的根,考查了数形结合数学,属于中档题.
9.【答案】ABD
【解析】解:对于A,E(aX+b)=aE(X+ba),故A正确;
对于B,D(aX+b)=a2D(X)=a2D(X+ba),故B正确;
对于C,D,D(X)=E(X2)−(E(X))2,故C错误;D正确.
故选:ABD.
根据已知条件,结合期望与方差的线性公式,即可求解.
本题主要考查期望与方差的线性公式,属于基础题.
10.【答案】CD
【解析】解:对于A,命题“∀x∈R,1x>0”的否定为“∃x∈R,1x≤0”或“x=0”,A错误;
对于B,命题“若x>1,则2x+1>5”的否定为“存在x>1,使2x+1≤5”,B错误;
对于C,x,y∈R,则“x或y为有理数”是“xy为有理数”的既不充分也不必要条件,
比如x=1,y=π,满足“x或y为有理数”,但xy=π是无理数,所以”x或y为有理数”是“xy为有理数”的不充分条件,再比如x= 2,y= 2,满足“xy为有理数”,但x,y都不是有理数,所以”x或y为有理数”是“xy为有理数”的不必要条件,所以“x或y为有理数”是“xy为有理数”的既不充分也不必要条件,C正确;
对于D,由于余弦函数为周期函数,所以若“x≠y”,不一定有“cosx≠cosy”,
“x≠y”是“cosx≠cosy”不充分条件,
若“cosx≠cosy”,则x,y必不相等,所以“x≠y”是“cosx≠cosy”的必要条件,
所以如果x,y是实数,则“x≠y”是“cosx≠cosy”的必要不充分条件,D正确.
故选:CD.
命题的否定是对命题结论的否定,相当于找命题的漏洞,由此分析各选项即可.
本题主要考查命题否定的概念以及充要条件,属中档题.
11.【答案】BCD
【解析】解:因为xy⋅y=x,
所以f(x)=f(xy⋅y)=f(xy)+f(y),
所以f(xy)=f(x)−f(y),故B正确;
所以f(xn)=f(x)+f(xn−1)=f(x)+f(x)+f(xn−2)=…=f(x)+f(x)+…+f(x)=nf(x),故C正确;
又因为x=(nx)n=nx×nx×nx×…×nx,
所以f(x)=f(nx)+f(nx)+…+f(nx)=nf(nx),故D正确;
对于A,由题意可设f(x)=lnx,x>0,
则f(x+y)=ln(x+y),
而f(x)f(y)=lnxlny≠ln(x+y),故A错误.
故选:BCD.
设函数f(x)=lnx,x>0判断A选项,结合有f(xy)=f(x)+f(y)判断B,C,D选项.
本题考查了抽象函数的应用、对数的基本运算及逻辑推理能力,属于中档题.
12.【答案】C
【解析】解:对于A,令f(x)=lnxln(x+1),则f′(x)=(x+1)ln(x+1)−xlnxx(x+1)ln2(x+1),
当x>1,显然(x+1)ln(x+1)−xlnx>0,x(x+1)ln2(x+1)>0,
所以f′(x)>0,f(x)单调递增,
所以有f(5)>f(3),即ln5ln6>ln3ln4,
即log65>log43,A错误;
对于B,令g(x)=ex−(1+x),h(x)=x−(lnx+1),
则g′(x)=ex−1,h′(x)=1−1x,
当0
又g(1)=0,h(1)=0,所以g(x)≥0,h(x)≥0,
所以有当x>0,x(ex−1+2)≥x(x+2)≥x2+2lnx+2,
由于等号在同一点取得,所以x(ex−1+2)≥x2+2lnx+2,当且仅当x=1,等号成立,
对于C,令I(x)=x−ln(x+1),同上可证明I(x)≥0,
结合上面分析所以有ex≥1+x≥ln(x+2),
由于等号不是在同一点取得,所以ex>ln(x+2),
当m≤2,自然有ex>ln(x+m),C正确;
对于D,由于sin(−π2)=−1>−π2,所以D错误.
故选:C.
构造函数并结合反例进行分析即可.
本题主要考查对数的比较,构造函数是解决本题的关键.
13.【答案】(0,1)和(1,32)
【解析】解:由题意得函数定义域为{x|x≠1},f′(x)=ex⋅[2x−1x−1+2(x−1)−(2x−1)(x−1)2]=ex⋅2x2−3x(x−1)2,
由f′(x)=0得x=0或x=32,由f′(x)<0得0
故答案为:(0,1)和(1,32).
由题意得函数定义域为{x|x≠1},f′(x)=ex⋅[2x−1x−1+2(x−1)−(2x−1)(x−1)2]=ex⋅2x2−3x(x−1)2,求出f′(x)<0的解集,即可得出答案.
本题考查利用导数研究函数的单调性,考查转化思想,考查逻辑推理能力和运算能力,属于中档题.
14.【答案】40
【解析】解:2160=24×33×5,它的正因数即为2,3,5的幂的乘积,
因此正因数个数为(4+1)×(3+1)×(1+1)=40,
故答案为:40.
把2160进行质因数分解,然后结合分步乘法原理计算.
本题考查分步计数原理,属于基础题.
15.【答案】4a+5b8
【解析】解:设销售价为x元/件,它比售价b元下降了10%,
从而x=b(1−10%),故b−xb=110,
由题意此时可卖出m件,则m=c(1+40%)=c+4c⋅b−xb,
从而利润L(x)=(x−a)( c+4c⋅b−xb)=c(x−a)(5−4bx),a
令L′(x)=0,解得x=4a+5b8,当x∈(a,4a+5b8)时,L′(x)>0;
当x∈(4a+5b8,5b4)时,L′(x)<0.
因此x=4a+5b8是函数L(x)的极大值点,也是最大值点.
则销售价为4a+5b8元/件时,可获得最大利润.
故答案为:4a+5b8.
设销售价为x元/件,它比售价b元下降了10%,根据x=b(1−10%),可得b−xb=110,从而可求出卖出c(1+40%)=c+4c⋅b−xb,得利润函数L(x)=(x−a)( c+4c⋅b−xb)=c(x−a)(5−4bx),a
16.【答案】n(n+1)2n−2
【解析】解:根据组合数公式可得k2Cnk=k2n!(n−k)!k!=nk(n−1)!(n−k)!(k−1)!=nkCn−1k−1,
kCn−1k=k(n−1)!(n−k−1)!k!=(n−1)⋅(n−2)!(n−k−1)!(k−1)!=(n−1)Cn−2k−1,
所以原式=n(Cn−10+2Cn−11+⋯+nCn−1n−1)
=n[Cn−10+Cn−11+⋯+Cn−1n−1+Cn−11+2Cn−12+⋯+(n−1)Cn−1n−1]
=n[2n−1+(n−1)(Cn−20+Cn−21+⋯+Cn−2n−2)
=n[2n−1+(n−1)2n−2]=n(n+1)2n−2.
故答案为:n(n+1)2n−2.
根据组合数公式可得k2Cnk=k2n!(n−k)!k!=nk(n−1)!(n−k)!(k−1)!=nkCn−1k−1,
kCn−1k=k(n−1)!(n−k−1)!k!=(n−1)⋅(n−2)!(n−k−1)!(k−1)!=(n−1)Cn−2k−1,再结合二项式系数和公式即可求解.
本题考查了二项式定理的应用计算,属于中档题.
17.【答案】解:(1)过点A作AE⊥BC,交BC的延长线于E,连接DE,
∵AB=BC=BD,∠CBA=∠CBD=120°,∴△CBA≌△CBD,
∴DE⊥BC,
∵平面ABC⊥平面BCD,且平面ABC∩平面BCD=BC,AE⊂平面ABC,
∴AE⊥平面BCD,
∵DE⊂平面BCD,EB⊂平面BCD,∴AE⊥DE,AE⊥BE,
∴ED,EB,EA两两垂直,
以E为坐标原点,建立如图所示的空间直角坐标系,
设AB=BC=BD=2,则BE=1,AE=DE= 3,
则A(0,0, 3),D( 3,0,0),E(0,0,0),
AD=( 3,0,− 3),
∵AE⊥平面BCD,∴平面BCD的一个法向量为EA=(0,0, 3),
设直线AD与平面BDC所成角的大小为θ,
则sinθ=|EA⋅AD||EA|⋅|AD|=3 3⋅ 6= 22,
∴θ∈[0,π2],∴θ=π4,
∴直线AD与平面BDC所成角的大小为π4.
(2)B(0,1,0),C(0,3,0),AB=(0,1,− 3),
设平面ABD的法向量为n=(x,y,z),
则n⋅AB=y− 3z=0n⋅AD= 3x− 3z=0,
令z=1,得n=(1, 3,1),
∴|cos
∴平面ABD和平面BDC夹角的余弦值为 55.
【解析】(1)过点A作AE⊥BC,交BC的延长线于E,连接DE,证明ED,EB,EA两两垂直,建立空间直角坐标系,利用空间向量求线面角的公式即可求出结果.
(2)利用向量法能求出平面ABD和平面BDC夹角的余弦值.
本题考查线面角的定义及求法、二面角的定义及余弦值的求法等基础知识,考查运算求解能力,是中档题.
18.【答案】(1)解:集合A={x|x2−(a+1)x+a=0,a∈R}={x|(x−1)(x−a)=0},
B={x|x2−5x+4=0}={x|(x−1)(x−4)=0}={1,4},
若a=1,则A={1},则A∩B={1},A∪B={1,4},
若a=4,则A=B={1,4},则A∩B={1,4},A∪B={1,4},
若a≠1,a≠4,则A={1,a},则A∩B={1},A∪B={1,a,4}.
(2)证明:因为x,y,z都是正数,x32+y32+z32=32,
所以x+y≥2 xy(当且仅当x=y时等号成立),
y+z≥2 yz(当且仅当y=z时等号成立),
z+x≥2 zx(当且仅当z=x时等号成立),
所以xy+z+yz+x+zx+y≤x2 yz+y2 zx+z2 xy=x32+y32+z322 xyz=322 xyz=34 xyz,(当且仅当x=y=z时等号成立)
故:xy+z+yz+x+zx+y≤34 xyz.
【解析】(1)先求集合中的元素,注意集合中元素的互异性,因此需要对a分类讨论,然后求集合的交集和并集;
(2)运用基本不等式,利用问题形式上的对称性,通过通分结合已知条件可以得证.
(1)考查集合的运算,注意集合中元素的互异性;(2)运用基本不等式解决问题需要观察问题的形式,适当地放缩.
19.【答案】解:(1)设数列{an}的公比为q,则a3=a1q2=32S3=a1+a1q+32=92 ,
解得a1=6,q=−12或a1=32,q=1,
所以an=6×(−12)n−1或an=32;
(2)设数列{bn}的公差为d,则bn=2+(n−1)d=dn+2−d,
所以Cn=n2bn=n2dn+2−d,即c1=12,c2=4d+2,c3=92d+2,
又数列{cn}为等差数列,所以c1+c3=2c2,
即12+92d+2=8d+2,解得d=2,
即bn=2n,cn=n2,
当an=6×(−12)n−1时,xn=6×(−12)n−1×2nn2=24×(−12)n−1,
所以xn+1xn=24×(−12)n24×(−12)n−1=−12,x1=24,
即数列{xn}是以24为首项,−12为公比的等比数列,
所以Tn=24×[1−(−12)n]1−(−12)=16−16×(−12)n;
当an=32时,xn=32×2nn2=6,所以Tn=6n.
综上所述,Tn=16−16×(−12)n或6n.
【解析】(1)设数列{an}的公比为q,化简a3和S3为基本量a1和q的关系,进而解出a1和q,从而求解;
(2)设数列{bn}的公差为d,可得bn=dn+2−d,cn=n2dn+2−d,进而根据等差数列{cn}的前三项成等差数列,可得d=2,从而得到bn,Cn,进而分an=6×(−12)n−1或an=32两种情况得到xn,进而求解即可.
本题考查等差数列和等比数列的综合应用,属中档题.
20.【答案】解:(1)设n(n∈N+)次传球后球在甲手中的概率为Pn,
则P1=0=02,P2=2−022,P3=22−(2−0)23,
即2nPn=2n−1−2n−1Pn−1(n≥2),整理得Pn−13=−12(Pn−1−13),
又P1−13=−13,所以数列{Pn−13}是以−13为首项,−12为公比的等比数列,
所以Pn−13=−13×(−12)n−1,即Pn=−13×(−12)n−1+13;
(2)设n(n∈N+)次传球后球在乙手中的概率为Qn,
Q1=12,Q2=2−122,Q3=22−(2−1)23,
又Q1−13=16,与(1)同理,数列{Qn−13}是以16为首项,−12为公比的等比数列,
所以Qn−13=16×(−12)n−1,即Qn=16×(−12)n−1+13;
(3)结合(1)可得E(Y)=−13×1−(−12)n1−(−12)+n3=29×(−12)n+n3−29.
【解析】(1)由于球是从甲开始传的,第一次传球后球在甲手中的概率为0即02,第二次球传到甲的概率为2−022,第三次球传到甲的概率为22−(2−0)23,之后以此类推;
(2)第一次传球后球在乙手中的概率为12,第二次球传到乙的概率为2−122,第三次球传到乙手中的概率为22−(2−1)23,之后的以此类推;
(3)结合(1)进行计算.
本题考查排列组合的应用,属于中档题.
21.【答案】解:(1)设动点为M,其坐标为(x,y),
当x≠±a时,由条件可得kMA1⋅kMA2=yx−a⋅yx+a=m,
即mx2−y2=ma2(x≠±a),
又A1(−a,0),A2(a,0)的坐标满足mx2−y2=ma2,
所以曲线C的方程为mx2−y2=ma2;
当m<−1时,曲线C的方程为x2a2+y2−ma2=1,C是焦点在y轴上的椭圆,
当m=−1时,曲线C的方程为x2+y2=a2,C是圆心在原点的圆,
当−1
(2)在C1上存在点N,使得△F1NF2的面积S=|m|a2,证明如下:
由(1)知,当m=−1时,曲线C1的方程为x2+y2=a2,
当m∈(−1,0)∪(0,+∞)时,C2的焦点分别为F1(−a 1+m,0),F2(a 1+m,0),
对于给定的m∈(−1,0)∪(0,+∞),C1上存在点N(x0,y0)(y0≠0),使得△F1NF2的面积S=|m|a2的充要条件为
x02+y02=a2①12×2a 1+m|y0|=|m|a2②
由①得0<|y0|≤a,由②得|y0|=|m|a 1+m,
所以0<|m|a 1+m≤a,解得1− 52≤m<0或0
【解析】(1)设动点为M,其坐标为(x,y),根据题意可得yx−a⋅yx+a=m,整理可得曲线C的方程为mx2−y2=ma2,再把方程化为标准方程即可判断曲线的类型;
(2)对于给定的m∈(−1,0)∪(0,+∞),C1上存在点N(x0,y0)(y0≠0),使得△F1NF2的面积S=|m|a2的充要条件为x02+y02=a212×2a 1+m|y0|=|m|a2,从而求得1− 52≤m<0或0
22.【答案】解:(1)设AB=x,由题意可知,矩形ABCD(AB>CD)的周长为6,所以AD=3−x,
由题意可知∠DCA=∠BAC=∠B′AC,所以PC=PA,
设PC=a,则DP=x−a,AP=a,而△ADP为直角三角形,
∴(3−x)²+(x−a)²=a²,∴a=x+92x−3,则DP=3−92x,
∴S△ADP=12×AD⋅DP=274−(274x+3x2)≤274−2 274x×3x2=274−9 22,
当且仅当274x=3x2时,即x=3 22,等号成立,此时AD=3−3 22满足AB>AD,
所以当AB=3 22,AD=3−3 22时,△ADP取最大面积为274−9 22.
(2)①当k=0时,此时A点与D点重合,折痕所在的直线方程y=12,折痕的长为2
②当k≠0时,将矩形折叠后A点落在线段CD上的点为G(a,1)(0
故G点坐标为G(−k,1)(−2≤k<0),
从而折痕所在的直线与OG的交点坐标(线段OG的中点)为M(−k2,12),
所以折痕所在的直线方程y−12=(x+k2),即y=kx+k22+12(−2≤k<0),
记PN²=y,
当折痕所在的直线过点D时,1=k22+12,解得k=−a(舍去k=−1),
当折痕所在的直线过点B时,0=2k+k22+12,解得k=−2+ 3(舍去k=−2− 3),
如图(1),折痕所在的直线与边AD、BC的交点坐标为N(0,k2+12),P(2,2k+k2+12),
这时−2+ 3
如图(2),折痕所在的直线与边AD、AB的交点坐标为N(0,k2+12),P(−k2+12k,0),
这时,−1≤k≤−2+ 3,y=(k2+12)2+(−k2+12k)2=(k2+1)34k2,
则y′=(k2+1)2(2k2−1)2k3,
令y′=0,得k=− 22,
所以当−1≤k<− 22时,y′>0,函数单调递增,
当− 22
当k=− 22时,y=2716;
当k=−2+ 3时,y=16(2− 3),
∴y∈[2716,16(2− 3)],
如图(3),折痕所在的直线与边CD、AB的交点坐标为N(1−k22k,1),P(−k2+12k,0),
这时−2≤k<−1,y=(1k)2+1∈[54,2),
综上所述,ymax=16(2− 3),即折痕的长度取最大值2( 6− 2),此时k=−2+ 3.
【解析】(1)设AB=x,PC=a,由题意可知,DP=x−a,AP=a,由△ADP为直角三角形得a=x+92x−3,再用三角形的面积公式求得△ADP的面积关于x的函数,再利用基本不等式即可求得最大值;
(2)对折痕所在直线的斜率分类讨论,斜率为0时,易得结论,斜率不为0时,又要分析折痕所在直线与矩形两边的交点在左右两边、上下两边、左下两边三种情况讨论,最后可解.
本题主要考查数形结合以及根据实际问题选择合适的函数模型,属于中档题.
2022-2023学年湖北省武汉外国语学校高二(下)期末数学试卷(含详细答案解析): 这是一份2022-2023学年湖北省武汉外国语学校高二(下)期末数学试卷(含详细答案解析),共17页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年湖北省武汉市新洲区部分学校高二(下)期末数学试卷(含解析): 这是一份2022-2023学年湖北省武汉市新洲区部分学校高二(下)期末数学试卷(含解析),共21页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年湖北省武汉市部分学校联合体高二(下)期末数学试卷(含解析): 这是一份2022-2023学年湖北省武汉市部分学校联合体高二(下)期末数学试卷(含解析),共19页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。












