辽宁省大连市西岗区2022-2023学年七年级下学期期末数学试卷（含答案）

这是一份辽宁省大连市西岗区2022-2023学年七年级下学期期末数学试卷（含答案），共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2022-2023学年辽宁省大连市西岗区七年级（下）期末数学试卷
学校:___________姓名：___________班级：___________考号：___________
第I卷（选择题）
一、选择题（本大题共10小题，共20.0分。在每小题列出的选项中，选出符合题目的一项）
1. 在-3，2，0，1四个数中，是无理数的是(    )
A. -3 B. 2 C. 0 D. 1
2. 下列各图中，∠1与∠2是对顶角的是(    )
A. B. C. D.
3. 下列调查中，适合采用全面调查方式的是(    )
A. 对付家庄水域水质情况的调查 B. 对端午节期间市场上粽子质量情况的调查
C. 对某班50名学生视力情况的调查 D. 对灯具厂家一批节能灯管使用寿命的调查
4. 下列四组数中是方程3x+y=5的解是(    )
A. x=2y=-1 B. x=-1y=2 C. x=2y=3 D. x=-2y=3
5. 在平面直角坐标系中，点P在x轴上方，y轴右侧，距离x轴2个单位长度，距离y轴4个单位长度，则点P坐标是(    )
A. (-2,4) B. (-4,2) C. (2,4) D. (4,2)
6. 下列说法正确的是(    )
A. 正数的平方根是它本身 B. 100的平方根是10
C. -10是100的一个平方根 D. -1的平方根是-1
7. 如图，直线a，b被直线c所截，若直线a/​/b，∠2=68°，则∠1的度数为(    )
A. 112°
B. 122°
C. 68°
D. 22°
8. 若a>b，则下列不等式成立的是(    )
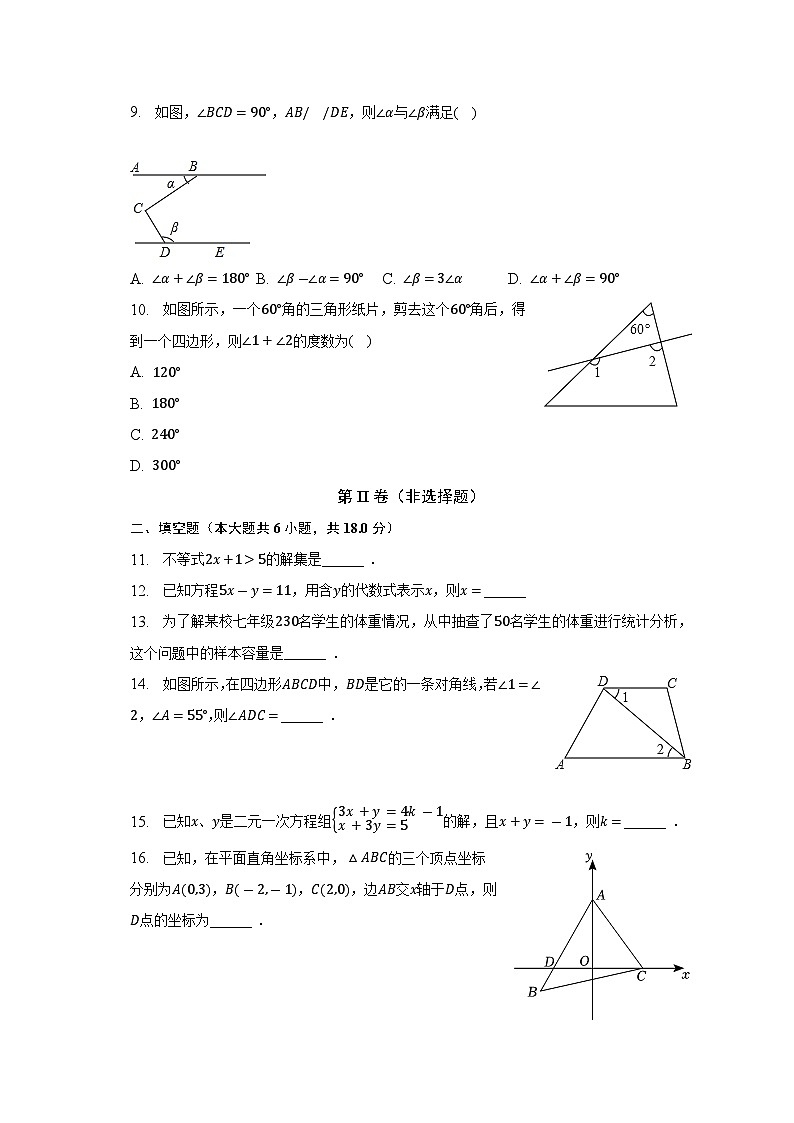
A. a+2b+3 C. -4a<-4b D. a2 9. 如图，∠BCD=90°，AB/​/DE，则∠α与∠β满足(    )


A. ∠α+∠β=180° B. ∠β-∠α=90° C. ∠β=3∠α D. ∠α+∠β=90°
10. 如图所示，一个60°角的三角形纸片，剪去这个60°角后，得到一个四边形，则∠1+∠2的度数为(    )
A. 120°
B. 180°
C. 240°
D. 300°
第II卷（非选择题）
二、填空题（本大题共6小题，共18.0分）
11. 不等式2x+1>5的解集是______ ．
12. 已知方程5x-y=11，用含y的代数式表示x，则x=______
13. 为了解某校七年级230名学生的体重情况，从中抽查了50名学生的体重进行统计分析，这个问题中的样本容量是______ ．
14. 如图所示，在四边形ABCD中，BD是它的一条对角线，若∠1=∠2，∠A=55°，则∠ADC=______ ．


15. 已知x、y是二元一次方程组3x+y=4k-1x+3y=5的解，且x+y=-1，则k=______ ．
16. 已知，在平面直角坐标系中，△ABC的三个顶点坐标分别为A(0,3)，B(-2,-1)，C(2,0)，边AB交x轴于D点，则D点的坐标为______ ．


三、解答题（本大题共9小题，共82.0分。解答应写出文字说明，证明过程或演算步骤）
17. (本小题10.0分)
(1)计算：(-3)2-36+327；
(2)解方程组：x+2y=93x-2y=-1；
18. (本小题5.0分)
解不等式组：2x+3≤x+62x+53<2+x，并把它的解集在数轴上表示出来．


19. (本小题8.0分)
如图，已知AB/​/CD，∠B+∠D=180°，求证：BC/​/DE．





20. (本小题8.0分)
大连某运输公司计划用大小两种货车将56吨救灾物资运往灾区，大货车每辆载重为6吨，小货车每辆载重为5吨，要求安排的车辆不超过10辆.问题：请通过你所学的知识说明大货车至少安排多少辆？
21. (本小题9.0分)
某校体育组对本校九年级全体同学体育测试情况进行调查，他们随机抽查部分同学体育测试成绩(由高到低分四个等级)，根据调查的数据绘制成如下的条形统计图和扇形统计图．

请根据以上不完整的统计图提供的信息，解答下列问题：
(1)该课题研究小组共抽查了______ 名同学的体育测试成绩，扇形统计图中B级所占的百分比b=______ ；
(2)补全条形统计图；
(3)若该校九年级共有200名同学，请估计该校九年级同学体育测试达标(测试成绩C级以上，含C级)均有______ 名．
22. (本小题9.0分)
如图，在平面直角坐标系中，将△ABC平移后得到△DEF，它们的各顶点坐标如表所示：
△ABC
A(-1,0)
B(2,0)
C(3,4)
△DEF
D(3,2)
E(6,a)
F(b,c)
(1)观察表中各对应点坐标的变化，可知将△ABC向______ 平移______ 个单位长度，再向______ 平移______ 个单位长度可以得到△DEF；
(2)在平面直角坐标系中画出平移后的△DEF；
(3)请直接写出△DEF的面积为______ ．


23. (本小题9.0分)
填空：如图，EF/​/AD，AD//BC，CE平分∠BCF，∠DAC=120°，∠ACF=20°．
求∠FEC的度数．
解：∵AD/​/BC
∴∠ACB+∠DAC=180°(______ )，
∵∠DAC=120°
∴∠ACB=180°-∠DAC=______ °.
∵∠AOF=20°，
∴∠BCF=______ °.
∵CE平分∠BCF，
∴∠BOE=12∠BCF=______ ．
∵EF/​/AD，AD//BC，
∴______ /​/______ (______ )，
∴∠FEC=∠BCE=______ °.(______ ).

24. (本小题12.0分)
西岗区某中学为落实《教育部办公厅关于进一步加强中小学生体质管理的通知》文件要求，决定增设篮球、足球两门选修课程，为此需要购进一批篮球和足球.已知购买2个篮球和3个足球需要510元；购买3个篮球和5个足球需要810元．
(1)根据以上信息解答若需要购买1个篮球和2个足球需要多少钱；
(2)学校计划采购篮球、足球共50个，并要求篮球不少于30个，且总费用不超过5500元，则有哪几种购买方案？
25. (本小题12.0分)
已知，如图，在平面直角坐标系中，A(0,m)，B(n,0)，AD平分∠OAB．
(1)若∠OAB=∠ODA，试判断∠ABO与∠OAD的数量关系，并说明理由；
(2)在(1)的条件下，P(t,0)为x轴正半轴上一动点(不与D点重合)，PM⊥直线AB于M，∠OPM的角平分线交直线AB与N，试判断直线AD与直线PN的位置关系，说明理由.并写出t的取值范围．


答案和解析

1.【答案】B 
【解析】解：-3，0，1是有理数，
2是无理数，
故选：B．
分别根据无理数、有理数的定义即可判定选择项．
此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，6，0.8080080008…(每两个8之间依次多1个0)等形式．

2.【答案】B 
【解析】解：A、∠1与∠2不是对顶角，故A选项错误；
B、∠1与∠2是对顶角，故B选项正确；
C、∠1与∠2不是对顶角，故C选项错误；
D、∠1与∠2不是对顶角，故D选项错误．
故选：B．
根据对顶角的定义对各选项分析判断后利用排除法求解．
本题主要考查了对顶角的定义，熟记对顶角的图形是解题的关键．

3.【答案】C 
【解析】解：A、对付家庄水域水质情况的调查，适合采用抽样调查，故A不符合题意；
B、对端午节期间市场上粽子质量情况的调查，适合采用抽样调查，故B不符合题意；
C、对某班50名学生视力情况的调查，适合采用全面调查，故C符合题意；
D、对灯具厂家一批节能灯管使用寿命的调查，适合采用抽样调查，故D不符合题意；
故选：C．
根据全面调查与抽样调查的特点，逐一判断即可解答．
本题考查了全面调查与抽样调查，熟练掌握全面调查与抽样调查的特点是解题的关键．

4.【答案】A 
【解析】解：A.当x=2y=-1时，左边=3x+y=5=右边，故符合题意；
B.当x=-1y=2时，左边=3x+y=1≠右边，故不符合题意；
C.当x=2y=3时，左边=3x+y=9≠右边，故不符合题意；
D.当x=-2y=3时，左边=3x+y=-3≠右边，故不符合题意；
故选：A．
把A、B、C、D中的解代入到方程3x+y=5，看方程左右是否相等．
本题主要考查了二元一次方程的解，解题的关键是把每个选项的解代入方程看是否成立．

5.【答案】D 
【解析】解：设点P的坐标为(x,y)，
∵在x轴上方，y轴右侧，
∴y>0，x>0，
∵距离x轴2个单位长度，距离y轴4个单位长度，
∴x=4，y=2，
∴P(4,2)，
故选：D．
设点P的坐标为(x,y)，再根据条件可得确定x、y的值，进而可得P点坐标．
此题主要考查了点的坐标，关键是掌握点距离x轴的距离等于纵坐标的绝对值，距离y轴的距离等于横坐标的绝对值．

6.【答案】C 
【解析】解：A、正数的平方根是它本身，错误；
B、100的平方根是10，错误，应为±10；
C、-10是100的一个平方根，正确；
D、-1没有平方根，故此选项错误；
故选：C．
直接利用平方根的性质分别分析得出答案．
此题主要考查了平方根，正确把握平方根的性质是解题关键．

7.【答案】A 
【解析】解：∵a/​/b，∠2=68°，
∴∠3=∠2=68°，
∵∠1+∠3=180°，
∴∠1=112°．
故选：A．
由a/​/b，∠2=68°，根据两直线平行，同位角相等，即可求得∠3的度数，又由邻补角的定义，即可求得∠1的度数．
此题考查了平行线的性质与邻补角的定义．解题的关键是注意掌握两直线平行，同位角相等定理的应用．

8.【答案】C 
【解析】解：A、由a>b知a+2 B、由a>b知a-3>b-3，此选项错误；
C、由a>b知-4a<-4b，此选项正确；
D、由a>b知a2>b2，此选项错误；
故选：C．
根据不等式的性质分别进行判断即可．
本题考查了不等式的性质：不等式两边同时加上或减去一个数，不等式不改变方向；不等式两边同时乘以或除以一个正数，不等式不改变方向；不等式两边同时乘以或乘以一个负数，不等式要改变方向．

9.【答案】B 
【解析】解：过C作CF/​/AB，
∵AB//DE，
∴AB/​/CF/​/DE，
∴∠1=∠α，∠2=180°-∠β，
∵∠BCD=90°，
∴∠1+∠2=∠α+180°-∠β=90°，
∴∠β-∠α=90°，
故选：B．
过C作CF/​/AB，根据平行线的性质得到∠1=∠α，∠2=180°-∠β，于是得到结论．
本题考查了平行线的性质，熟记平行线的性质是解题的关键．

10.【答案】C 
【解析】
【分析】
三角形纸片中，剪去其中一个60°的角后变成四边形，则根据四边形的内角和等于360°即可求得∠1+∠2的度数．
主要考查了三角形及四边形的内角和，属于基础题．
【解答】
解：根据三角形的内角和定理得：
三角形纸片去掉60°的角后的两角的度数为180°-60°=120°，
在所剩四边形中，
∠1+∠2=360°-120°=240°．
故选：C．  
11.【答案】x>-3 
【解析】解：2x+1>-5，
∴2x>-6，
∴x>-3．
故答案为：x>-3．
首先移项，然后合并，最后化系数为1即可求解．
本题考查了解简单不等式的能力，解答这类题学生往往在解题时不注意移项要改变符号这一点而出错．
解不等式要依据不等式的基本性质：
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变；
(2)不等式的两边同时乘以或除以同一个正数乘以或除以同一个正数不等号的方向不变；
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变．

12.【答案】y+115． 
【解析】解：∵5x-y=11，
∴x=y+115，
故答案为：y+115．
根据等式的性质进行变形即可．
本题考查解二元一次方程，掌握等式的性质是正确解答的关键．

13.【答案】50 
【解析】解：为了解某校七年级230名学生的体重情况，从中抽查了50名学生的体重进行统计分析，这个问题中的样本容量是50，
根据总体、个体、样本、样本容量的意义，即可解答．
本题考查了总体、个体、样本、样本容量，熟练掌握这些数学概念是解题的关键．

14.【答案】125° 
【解析】解：∵∠1=∠2，
∴CD/​/AB，
∴∠A+∠ADC=180°，
∵∠A=55°，
∴∠ADC=125°．
故答案是：125°．
利用平行线的判定和性质即可解决问题．
本题主要考查了平行线的判断和性质．判定定理要掌握：内错角相等，两直线平行．

15.【答案】-2 
【解析】解：将方程组中的两个方程相加得，4x+4y=4k+4，
即x+y=k+1，
又∵x+y=-1，
∴k+1=-1，
即k=-2，
故答案为：-2．
根据二元一次方程组的解法将方程组中的两个方程相加得出4x+4y=4k+4，即x+y=k+1，再代入计算即可．
本题考查二元一次方程的解，理解二元一次方程解的定义，掌握二元一次方程的解法是正确解答的前提．

16.【答案】(-32,0) 
【解析】解：设直线AB的解析式为y=kx+b(k≠0)，
∵A(0,3)，B(-2,-1)，
∴b=3-2k+b=-1，
解得k=2b=3，
∴直线AB的解析式为y=2x+3，
当y=0时，x=-32，
∴D(-32,0)．
故答案为：(-32,0)．
利用待定系数法求出直线AB的解析式，求出D点坐标即可．
本题考查的是一次函数图象上点的坐标特点，坐标与图形性质，根据题意得出直线AB的解析式是解题的关键．

17.【答案】解：(1)原式=9-6+3
=6；
(2)x+2y=9①3x-2y=-1②，
①+②得：4x=8，
解得：x=2，
把x=2代入①得：2+2y=9，
解得：y=72，
则方程组的解为x=2y=72． 
【解析】(1)原式利用立方根，平方根定义以及平方的意义计算即可得到结果；
(2)方程组利用加减消元法求出解即可．
此题考查了实数的运算，解二元一次方程组，熟练掌握二元一次方程组的方法是解本题的关键．

18.【答案】解：2x+3≤x+6①2x+53<2+x②
解不等式①得，x≤3，
解不等式②得，x>-1，
不等式组的解集为-1 在数轴上表示为：
． 
【解析】分别求出各不等式的解集，再求出其公共解集并在数轴上表示出来即可．
本题考查的是在数轴上表示一元一次不等式组的解集，解答此类题目的关键是熟知实心圆点与空心圆点的区别．

19.【答案】证明：∵AB/​/CD，
∴∠B=∠C，
∵∠B+∠D=180°，
∴∠C+∠D=180°，
∴BC/​/DE． 
【解析】本题考查平行线的判定和性质，解答本题的关键是明确题意，找出所求问题需要的条件，利用平行线的性质和判定证明．
根据平行线的性质和判定可以解答本题．

20.【答案】解：设安排x辆大货车，则安排56-6x5辆小货车，
根据题意得：x+56-6x5≤10，
解得：x≥6，
又∵x，56-6x5均为正整数，
∴x的最小值为6．
答：大货车至少安排6辆． 
【解析】设安排x辆大货车，则安排56-6x5辆小货车，根据安排的车辆不超过10辆，可列出关于x的一元一次不等式，解之可得出x的取值范围，再结合x，56-6x5均为正整数，即可得出x的最小值，此题得解．
本题考查了一元一次不等式的应用，根据各数量之间的关系，正确列出一元一次不等式是解题的关键．

21.【答案】80；40%；190 
【解析】解：(1)根据题意得：20÷25%=80(人)，
B占的百分比为3280×100%=40%；           

(2)C级的人数为80-(20+32+4)=24(人)，补全条形图，如图所示：


(3)根据题意得：200×20+32+2480=190(人)，
则估计该校九年级同学体育测试达标的人数约为190人．
(1)由等级A的人数除以所占的百分比求出调查的总学生；进一步求出B占的百分比；
(2)求出C级的学生数，补全条形统计图即可；
(3)求出A，B，C的百分比之和，乘以600即可得到结果．
此题考查了条形统计图，扇形统计图，以及用样本估计总体，弄清题意，从统计图中得到必要的信息是解决问题的关键．

22.【答案】右  4  上  2  6 
【解析】解：(1)观察表中各对应点坐标的变化，可知将△ABC向右平移4个单位长度，再向上平移2个单位长度可以得到△DEF．
故答案为：右，4，上，2；
(2)如图，△DEF即为所求；
(3)请直接写出△DEF的面积=12×3×4=6．
故答案为：6．

(1)根据平移变换的性质判断即可；
(2)利用平移变换的性质画出图形即可；
(3)利用三角形面积公式求解．
本题考查作图-平移变换，三角形的面积等知识，解题的关键是理解题意，灵活运用所学知识解决问题．

23.【答案】两直线平行，同旁内角互补  60  40  20  EF  BC  平行于同一直线的两直线平行  20  两直线平行，内错角相等 
【解析】解：∵AD/​/BC(已知)，
∴∠ACB+∠DAC=180° (两直线平行，同旁内角互补)，
∵∠DAC=120°(已知)，
∴∠ACB=180°-∠DAC=60°，
∵∠ACF=20°(已知)，
∴∠BCF=∠ACB-∠ACF=40°，
∵CE平分∠BCF，
∴∠BCE=12∠BCF=20°，
∵EF/​/AD，AD//BC，
∴EF//BC (平行于同一直线的两直线平行)，
∴∠FEC=∠BCE=20°(两直线平行，内错角相等)．
故答案为：两直线平行；同旁内角互补；60；40；20；EF；BC；平行于同一直线的两直线平行；20；两直线平行，内错角相等．
根据平行线的性质求出∠ACB，求出∠BCF，根据角平分线性质求出∠BCE，根据平行线的性质求出即可．
本题考查了平行线的性质和判定，平行公理及推论的运用，平行线的性质有：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补．

24.【答案】解：(1)设篮球的单价是x元，足球的单价是y元，
根据题意得：2x+3y=5103x+5y=810，
解得：x=120y=90，
∴x+2y=120+2×90=300．
答：购买1个篮球和2个足球需要300元；
(2)设购买m个篮球，则购买(50-m)个足球，
根据题意得：m≥30120m+90(50-m)≤5500，
解得：30≤m≤1003，
又∵m为正整数，
∴m可以为30，31，32，33，
∴共有4种购买方案，
方案1：购买30个篮球，20个足球；
方案2：购买31个篮球，19个足球；
方案3：购买32个篮球，18个足球；
方案4：购买33个篮球，17个足球． 
【解析】(1)设篮球的单价是x元，足球的单价是y元，根据“购买2个篮球和3个足球需要510元；购买3个篮球和5个足球需要810元”，可列出关于x，y的二元一次方程组，解之可求出x，y的值，再将其代入(x+2y)中，即可求出结论；
(2)设购买m个篮球，则购买(50-m)个足球，根据“购进篮球不少于30个，且总费用不超过5500元”，可列出关于m的一元一次不等式组，解之可得出m的取值范围，再结合m为正整数，即可得出各购买方案．
本题考查了二元一次方程组的应用以及一元一次不等式组的应用，解题的关键是：(1)找准等量关系，正确列出二元一次方程组；(2)根据各数量之间的关系，正确列出一元一次不等式组．

25.【答案】解：(1)∠ABO=∠OAD．
证明：∵AD平分∠OAB，∠OAB=∠ODA，
∴12∠OAB+∠ABO=∠ODA=∠OAB，
∴∠ABO=12∠OAB=∠OAD．
∴∠ABO=∠OAD．
(2)①当点P在线段OB上时，即0 证明：∵∠ABO=∠OAD，
∴∠ODA=∠ABO+∠BAD，
又∵∠BAD=∠OAD，
∴∠ODA=2∠ABO．
又∵∠OAD+∠ODA=90°，∠ABO+∠BPM=90°，∠ABO=∠OAD，
∴∠ODA=2∠ABO=∠BPM．
又∵∠BPM+∠ABO=90°，
∴3∠ABO=90°，
∴∠ABO=30°．
∴∠OPN=180°-∠BPM2=180°-2×30°2=60°．
∴∠ODA=2∠ABO=2×30°=60°．
∵∠OPN=∠ODA=60°，
∴AD//PN．
②当点P在OB延长线上时，即t>n时，AD⊥PN．
证明：延长AB，过点P作AB延长线的垂线，交于点M.过点P作∠OPM的平分线PN，交AM于点N.PN的延长线与AD的延长线交于点Q．

∵∠ABO=∠PBM，∠AOB=PMB=90°，
∴∠OAB=MPB，
∴∠QAN=∠MPN，
又∵∠ANQ=∠PNM，
∴∠AQN=∠PMN=90°，
∴AD⊥PN． 
【解析】(1)根据已知条件和各角之间关系即可得到∠ABO与∠OAD的数量关系；
(2)分两种情况进行分析，即当0n时，分别判断直线AD与直线PN的位置关系．
本题考查坐标与图形的性质，解答过程比较繁琐，全是角之间的关系．