2023年中考数学真题分类汇编——专题20 图形的旋转（全国通用）

这是一份2023年中考数学真题分类汇编——专题20 图形的旋转（全国通用），文件包含专题20图形的旋转解析版docx、专题20图形的旋转原卷版docx等2份试卷配套教学资源，其中试卷共81页， 欢迎下载使用。

专题20 图形的旋转

一、单选题
1．（2023·江苏无锡·统考中考真题）如图，中，，将逆时针旋转得到，交于F．当时，点D恰好落在上，此时等于（    ）
  
A． B． C． D．
【答案】B
【分析】根据旋转可得，再结合旋转角即可求解．
【详解】解：由旋转性质可得：，，
∵，
∴，，
∴，
故选：B．
【点睛】本题考查了几何—旋转问题，掌握旋转的性质是关键．
2．（2023·天津·统考中考真题）如图，把以点A为中心逆时针旋转得到，点B，C的对应点分别是点D，E，且点E在的延长线上，连接，则下列结论一定正确的是（    ）
  
A． B． C． D．
【答案】A
【分析】根据旋转的性质即可解答．
【详解】根据题意，由旋转的性质，
可得，，，故B选项和D选项不符合题意，


，故C选项不符合题意，



，故A选项符合题意，
故选：A．
【点睛】本题考查了旋转的性质，熟练掌握旋转的性质和三角形外角运用是解题的关键．
3．（2023·四川宜宾·统考中考真题）如图，和是以点为直角顶点的等腰直角三角形，把以为中心顺时针旋转，点为射线、的交点．若，．以下结论：
①；②；
③当点在的延长线上时，；
④在旋转过程中，当线段最短时，的面积为．
其中正确结论有（　　）
  
A．1个 B．2个 C．3个 D．4个
【答案】D
【分析】证明即可判断①，根据三角形的外角的性质得出②，证明得出，即可判断③；以为圆心，为半径画圆，当在的下方与相切时，的值最小，可得四边形是正方形，在中，然后根据三角形的面积公式即可判断④．
【详解】解：∵和是以点为直角顶点的等腰直角三角形，
∴，
∴，
∴，
∴，，故①正确；
设，
∴,
∴，
∴，故②正确；
当点在的延长线上时，如图所示
  
∵，，
∴
∴
∵，．
∴，
∴
∴，故③正确；
④如图所示，以为圆心，为半径画圆，
  
∵，
∴当在的下方与相切时，的值最小，
∴四边形是矩形，
又，
∴四边形是正方形，
∴，
∵，
∴，
在中，
∴取得最小值时，
∴
故④正确，
故选：D．
【点睛】本题考查了旋转的性质，相似三角形的性质，勾股定理，切线的性质，垂线段最短，全等三角形的性质与判定，正方形的性质，熟练掌握以上知识是解题的关键．
4．（2023·山东聊城·统考中考真题）如图，已知等腰直角，，，点C是矩形与的公共顶点，且，；点D是延长线上一点，且．连接，，在矩形绕点C按顺时针方向旋转一周的过程中，当线段达到最长和最短时，线段对应的长度分别为m和n，则的值为（    ）
  
A．2 B．3 C． D．
【答案】D
【分析】根据锐角三角函数可求得，当线段达到最长时，此时点在点的下方，且，，三点共线，求得，，根据勾股定理求得，即，当线段达到最短时，此时点在点的上方，且，，三点共线，则，，根据勾股定理求得，即，即可求得．
【详解】∵为等腰直角三角形，，∴，
当线段达到最长时，此时点在点的下方，且，，三点共线，如图：
  
则，，
在中，，
即，
当线段达到最短时，此时点在点的上方，且，，三点共线，如图：
  
则，，
在中，，
即，
故，
故选：D．
【点睛】本题考查了锐角三角函数，勾股定理等，根据旋转推出线段最长和最短时的位置是解题的关键．

二、填空题
5．（2023·江苏连云港·统考中考真题）以正五边形的顶点C为旋转中心，按顺时针方向旋转，使得新五边形的顶点落在直线上，则正五边旋转的度数至少为______°．

【答案】
【分析】依据正五边形的外角性质，即可得到的度数，进而得出旋转的角度．
【详解】解：∵五边形是正五边形，

∴，
∴新五边形的顶点落在直线上，则旋转的最小角度是，
故答案为：．
【点睛】本题主要考查了正多边形、旋转性质，关键是掌握正多边形的外角和公式的运用．

6．（2023·湖南张家界·统考中考真题）如图，为的平分线，且，将四边形绕点逆时针方向旋转后，得到四边形，且，则四边形旋转的角度是______．
  
【答案】
【分析】根据角平分线的性质可得，根据旋转的性质可得，，求得，即可求得旋转的角度．
【详解】∵为的平分线，，
∴，
∵将四边形绕点逆时针方向旋转后，得到四边形，
∴，，
∴，
故答案为：．
【点睛】本题考查了角平分线的性质，旋转的性质，熟练掌握以上性质是解题的关键．
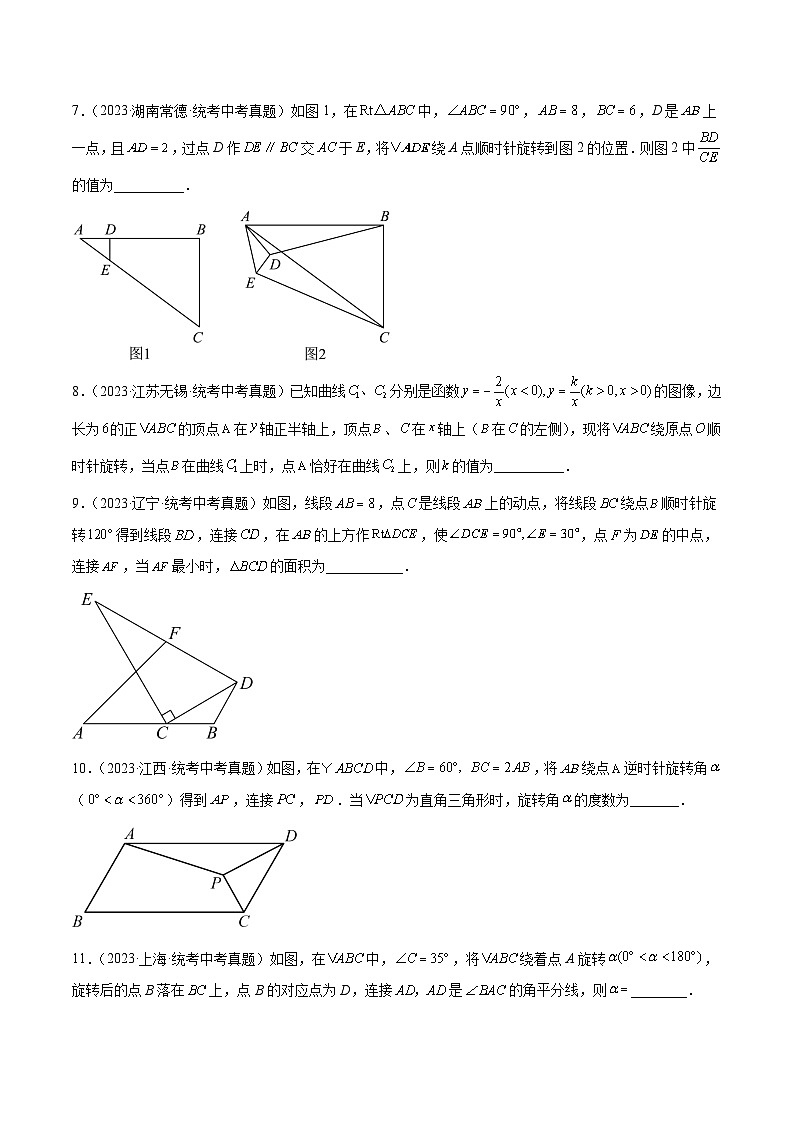
7．（2023·湖南常德·统考中考真题）如图1，在中，，，，D是上一点，且，过点D作交于E，将绕A点顺时针旋转到图2的位置．则图2中的值为__________．
  
【答案】
【分析】首先根据勾股定理得到，然后证明出，得到，进而得到，然后证明出，利用相似三角形的性质求解即可．
【详解】∵在中，，，，
∴
∵
∴，
∴
∴
∴
∵
∴
∴
∴
∴．
故答案为：．
【点睛】此题考查了相似三角形的性质和判定，解题的关键是熟练掌握相似三角形的性质和判定定理．
8．（2023·江苏无锡·统考中考真题）已知曲线分别是函数的图像，边长为的正的顶点在轴正半轴上，顶点、在轴上（在的左侧），现将绕原点顺时针旋转，当点在曲线上时，点恰好在曲线上，则的值为__________．
【答案】6
【分析】画出变换后的图像即可（画即可），当点在轴上，点、在轴上时，根据为等边三角形且，可得，过点、分别作轴垂线构造相似，则，根据相似三角形的性质得出，进而根据反比例函数的几何意义，即可求解．
【详解】当点在轴上，点、在轴上时，连接，
为等边三角形且，则，
，
如图所示，过点分别作轴的垂线，交轴分别于点，
，，
，
，
，
，
，
．

【点睛】本题考查了反比例函数的性质，的几何意义，相似三角形的性质与判定，正确作出辅助线构造相似三角形是解题关键．
9．（2023·辽宁·统考中考真题）如图，线段，点是线段上的动点，将线段绕点顺时针旋转得到线段，连接，在的上方作，使，点为的中点，连接，当最小时，的面积为___________．
  
【答案】
【分析】连接，交于点P，由直角三角形的性质及等腰三角形的性质可得垂直平分，为定角，可得点F在射线上运动，当时，最小，由含30度角直角三角形的性质即可求解．
【详解】解：连接，交于点P，如图，
∵，点为的中点，
∴，
∵，
∴,
∴是等边三角形，
∴；
∵线段绕点顺时针旋转得到线段，
∴，
∵，
∴垂直平分，，
∴点F在射线上运动，
∴当时，最小，
此时，
∴；
∵，
∴，
∴，
∵，
∴由勾股定理得，
∴，
∴；
  
故答案为：．
【点睛】本题考查了等腰三角形性质，含30度直角三角形的性质，斜边中线性质，勾股定理，线段垂直平分线的判定，勾股定理，旋转的性质，确定点F的运动路径是关键与难点．
10．（2023·江西·统考中考真题）如图，在中，，将绕点逆时针旋转角（）得到，连接，．当为直角三角形时，旋转角的度数为_______．
  
【答案】或或
【分析】连接，根据已知条件可得，进而分类讨论即可求解．
【详解】解：连接，取的中点，连接，如图所示，
  
∵在中，，
∴，
∴是等边三角形，
∴，，
∴
∴，
∴
∴，
如图所示，当点在上时，此时，则旋转角的度数为，
    
当点在的延长线上时，如图所示，则
  
当在的延长线上时，则旋转角的度数为，如图所示，
∵，，
∴四边形是平行四边形，
∵
∴四边形是矩形，
∴
即是直角三角形，
  
综上所述，旋转角的度数为或或
故答案为：或或．
【点睛】本题考查了平行四边形的性质与判定，等边三角形的性质与判定，矩形的性质与判定，旋转的性质，熟练掌握旋转的性质是解题的关键．
11．（2023·上海·统考中考真题）如图，在中，，将绕着点A旋转，旋转后的点B落在上，点B的对应点为D，连接是的角平分线，则________．
  
【答案】
【分析】如图，，，根据角平分线的定义可得，根据三角形的外角性质可得，即得，然后根据三角形的内角和定理求解即可．
【详解】解：如图，根据题意可得：，，
∵是的角平分线，
∴，
∵，，
∴，
则在中，∵，
∴，
解得：；
故答案为：
  
【点睛】本题考查了旋转的性质、等腰三角形的性质、三角形的外角性质以及三角形的内角和等知识，熟练掌握相关图形的性质是解题的关键．
12．（2023·湖南郴州·统考中考真题）如图，在中，，，．将绕点逆时针旋转，得到，若点的对应点恰好落在线段上，则点的运动路径长是___________cm（结果用含的式子表示）．
  
【答案】
【分析】由于旋转到，故C的运动路径长是的圆弧长度，根据弧长公式求解即可．
【详解】以A为圆心作圆弧，如图所示．
  
在直角中，，则，
则．
∴．
由旋转性质可知，，又，
∴是等边三角形．
∴．
由旋转性质知，．
故弧的长度为：；
故答案为：
【点睛】本题考查了含角直角三角形的性质、勾股定理、旋转的性质、弧长公式等知识点，解题的关键是明确C点的运动轨迹．
13．（2023·内蒙古·统考中考真题）如图，在中，，将绕点A逆时针方向旋转，得到．连接，交于点D，则的值为________．
  
【答案】5
【分析】过点D作于点F，利用勾股定理求得，根据旋转的性质可证、是等腰直角三角形，可得，再由，得，证明，可得，即，再由，求得，从而求得，，即可求解．
【详解】解：过点D作于点F，
∵，，，
∴，
∵将绕点A逆时针方向旋转得到，
∴，，
∴是等腰直角三角形，
∴，
又∵，
∴，
∴是等腰直角三角形，
∴，
∵，即，
∵ ，，
∴，
∴，即，
又∵，
∴，
∴，，
∴，
故答案为：5．
  
【点睛】本题考查旋转的性质、等腰三角形的判定与性质、相似三角形的判定与性质、三角形的面积，熟练掌握相关知识是解题的关键．
14．（2023·黑龙江绥化·统考中考真题）已知等腰，，．现将以点为旋转中心旋转，得到，延长交直线于点D．则的长度为_______．
【答案】
【分析】根据题意，先求得，当以点为旋转中心逆时针旋转，过点作交于点，当以点为旋转中心顺时针旋转，过点作交于点，分别画出图形，根据勾股定理以及旋转的性质即可求解．
【详解】解：如图所示，过点作于点，
  
∵等腰，，．
∴，
∴，,
∴，
如图所示，当以点为旋转中心逆时针旋转，过点作交于点，
      
∵，
∴，，
在中，，，
∵等腰，，．
∴，
∵以点为旋转中心逆时针旋转，
∴，
∴，
在中，,
∴，
∴，
∴，
如图所示，当以点为旋转中心顺时针旋转，过点作交于点，
  
在中，，
∴
在中，
∴
∴
∴
∴
∴，
综上所述，的长度为或，
故答案为：或．
【点睛】本题考查了旋转的性质，勾股定理，含30度角的直角三角形的性质，熟练掌握旋转的性质，分类讨论是解题的关键．
15．（2023·浙江嘉兴·统考中考真题）一副三角板和中，．将它们叠合在一起，边与重合，与相交于点G（如图1），此时线段的长是___________，现将绕点按顺时针方向旋转（如图2），边与相交于点H，连结，在旋转到的过程中，线段扫过的面积是___________．
  
【答案】 ；
【分析】如图1，过点G作于H，根据含直角三角形的性质和等腰直角三角形的性质得出，，然后由可求出的长，进而可得线段的长；如图2，将绕点C顺时针旋转得到，与交于，连接，，是旋转到的过程中任意位置，作于N，过点B作交的延长线于M，首先证明是等边三角形，点在直线上，然后可得线段扫过的面积是弓形的面积加上的面积，求出和，然后根据线段扫过的面积列式计算即可．
【详解】解：如图1，过点G作于H，
  
∵，，
∴，，
∵，
∴，
∴；
如图2，将绕点C顺时针旋转得到，与交于，连接，
由旋转的性质得：，，
∴是等边三角形，
∵，
∴，
∴，
∵，
∴，即垂直平分，
∵是等腰直角三角形，
∴点在直线上，
连接，是旋转到的过程中任意位置，
则线段扫过的面积是弓形的面积加上的面积，
∵，
∴，
∴，
作于N，则，
∴，
过点B作交的延长线于M，则，
∵，，
∴，
∴，
∴线段扫过的面积，
，
，
，
故答案为：，．
  
【点睛】本题主要考查了旋转的性质，含直角三角形的性质，二次根式的运算，解直角三角形，等边三角形的判定和性质，勾股定理，扇形的面积计算等知识，作出图形，证明点在直线上是本题的突破点，灵活运用各知识点是解题的关键．

三、解答题
16．（2023·北京·统考中考真题）在中、，于点M，D是线段上的动点（不与点M，C重合），将线段绕点D顺时针旋转得到线段．
    
(1)如图1，当点E在线段上时，求证：D是的中点；
(2)如图2，若在线段上存在点F（不与点B，M重合）满足，连接，，直接写出的大小，并证明．
【答案】(1)见解析
(2)，证明见解析
【分析】（1）由旋转的性质得，，利用三角形外角的性质求出，可得，等量代换得到即可；
（2）延长到H使，连接，，可得是的中位线，然后求出，设，，求出，证明，得到，再根据等腰三角形三线合一证明即可．
【详解】（1）证明：由旋转的性质得：，，
∵，
∴，
∴，
∴，
∴，即D是的中点；
（2）；
证明：如图2，延长到H使，连接，，
∵，
∴是的中位线，
∴，，
由旋转的性质得：，，
∴，
∵，
∴，是等腰三角形，
∴，，
设，，则，，
∴，
∴，
∵，
∴，
∴，
∴，
在和中，，
∴，
∴，
∵，
∴，即．
  
【点睛】本题考查了等腰三角形的判定和性质，旋转的性质，三角形外角的性质，三角形中位线定理以及全等三角形的判定和性质等知识，作出合适的辅助线，构造出全等三角形是解题的关键．
17．（2023·四川自贡·统考中考真题）如图1，一大一小两个等腰直角三角形叠放在一起，，分别是斜边，的中点，．
  
(1)将绕顶点旋转一周，请直接写出点，距离的最大值和最小值；
(2)将绕顶点逆时针旋转（如图），求的长．
【答案】(1)最大值为，最小值为
(2)
【分析】（1）根据直角三角形斜边上的中线，得出的值，进而根据题意求得最大值与最小值即可求解；
（2）过点作，交的延长线于点，根据旋转的性质求得，进而得出，进而可得，勾股定理解，即可求解．
【详解】（1）解：依题意，，，
当在的延长线上时，的距离最大，最大值为，
当在线段上时，的距离最小，最小值为；
  
（2）解：如图所示，过点作，交的延长线于点，
  
∵绕顶点逆时针旋转，
∴，
∵，
∴，
∴，
∴，
∴，
在中，，
在中，，
∴．
【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半，勾股定理，旋转的性质，含30度角的直角三角形的性质，熟练掌握旋转的性质，勾股定理是解题的关键．
18．（2023·四川达州·统考中考真题）如图，网格中每个小正方形的边长均为1，的顶点均在小正方形的格点上．
  
(1)将向下平移3个单位长度得到，画出；
(2)将绕点顺时针旋转90度得到，画出；
(3)在（2）的运动过程中请计算出扫过的面积．
【答案】(1)见解析
(2)见解析
(3)
【分析】（1）先作出点A、B、C平移后的对应点，、，然后顺次连接即可；
（2）先作出点A、B绕点顺时针旋转90度的对应点，，然后顺次连接即可；
（3）证明为等腰直角三角形，求出，，根据旋转过程中扫过的面积等于的面积加扇形的面积即可得出答案．
【详解】（1）解：作出点A、B、C平移后的对应点，、，顺次连接，则即为所求，如图所示：
  
（2）解：作出点A、B绕点顺时针旋转90度的对应点，，顺次连接，则即为所求，如图所示：
  
（3）解：∵，，，
∴，
∵，
∴，
∴为等腰直角三角形，
∴，
根据旋转可知，，
∴，
∴在旋转过程中扫过的面积为．
  
【点睛】本题主要考查了平移、旋转作图，勾股定理逆定理，扇形面积计算，解题的关键是作出平移或旋转后的对应点．
19．（2023·辽宁·统考中考真题）在中，，，点为的中点，点在直线上（不与点重合），连接，线段绕点逆时针旋转，得到线段，过点作直线，过点作，垂足为点，直线交直线于点．

(1)如图，当点与点重合时，请直接写出线段与线段的数量关系；
(2)如图，当点在线段上时，求证：；
(3)连接，的面积记为，的面积记为，当时，请直接写出的值．
【答案】(1)
(2)见解析
(3)或
【分析】（1）可先证，得到，根据锐角三角函数，可得到和的数量关系，进而得到线段与线段的数量关系．
（2）可先证，得到，进而得到，问题即可得证．
（3）分两种情况：①点D在线段上，过点作垂直于，交于点，过点作垂直于，交于点，设，利用勾股定理，可用含的代数式表示，根据三角形面积公式，即可得到答案．②点D在线段的延长线上，过点作垂直于，交延长线于点,令交于点,连接,设，可证，进一步证得是等腰直角三角形，，利用勾股定理，可用含的代数式表示，根据三角形面积公式，即可得到答案
【详解】（1）解：．
理由如下：
如图，连接．

根据图形旋转的性质可知．
由题意可知，为等腰直角三角形，
为等腰直角三角形斜边上的中线，
，．
又，
．
在和中，

．
，．
．
．
．
（2）解：为等腰直角三角形斜边上的中线，
．
，
．
，，
．
，．
，．
在和中，

．
．
．
（3）解：当点D在线段延长线上时，不满足条件，故分两种情况：
①点D在线段上，如图，过点作垂直于，交于点；过点作垂直于，交于点．

设，则．
根据题意可知，四边形和为矩形，为等腰直角三角形．
，．
由（2）证明可知，
．
．
．
根据勾股定理可知
，
的面积与的面积之比

②点D在线段的延长线上，过点作垂直于，交延长线于点,令交于点,连接,由题意知，四边形，是矩形，

∵
∴
即
又∵，
∴
∴
而
∴

∴是等腰直角三角形，
设，则，
∴
中，
的面积与的面积之比

【点睛】本题主要考查全等三角形的判定及性质、勾股定理以及图形旋转的性质，灵活利用全等三角形的判定及性质是解题的关键．


20．（2023·四川乐山·统考中考真题）在学习完《图形的旋转》后，刘老师带领学生开展了一次数学探究活动
【问题情境】
刘老师先引导学生回顾了华东师大版教材七年级下册第页“探索”部分内容：
如图，将一个三角形纸板绕点逆时针旋转到达的位置，那么可以得到：，，；，，（    ）
  
刘老师进一步谈到：图形的旋转蕴含于自然界的运动变化规律中，即“变”中蕴含着“不变”，这是我们解决图形旋转的关键；故数学就是一门哲学．
【问题解决】
（1）上述问题情境中“（    ）”处应填理由：____________________；
（2）如图，小王将一个半径为，圆心角为的扇形纸板绕点逆时针旋转到达扇形纸板的位置．
  
①请在图中作出点；
②如果，则在旋转过程中，点经过的路径长为__________；
【问题拓展】
小李突发奇想，将与（2）中完全相同的两个扇形纸板重叠，一个固定在墙上，使得一边位于水平位置，另一个在弧的中点处固定，然后放开纸板，使其摆动到竖直位置时静止，此时，两个纸板重叠部分的面积是多少呢？如图所示，请你帮助小李解决这个问题．
  
【答案】问题解决（1）旋转前后的图形对应线段相等，对应角相等
（2）①见解析；②
问题拓展：
【分析】问题解决（1）根据旋转性质得出旋转前后的图形对应线段相等，对应角相等；
（2）①分别作和的垂直平分线，两垂直平分线的交点即为所求点O；②根据弧长公式求解即可；
问题拓展，连接，交于，连接，，，由旋转得，，在和中求出和的长，可以求出，再证明，即可求出最后结果．
【详解】解：【问题解决】（1）旋转前后的图形对应线段相等，对应角相等                  
（2）①下图中，点O为所求                 
  
②连接，，
扇形纸板绕点逆时针旋转到达扇形纸板的位置，
，,
，
设，
，
，
在旋转过程中，点经过的路径长为以点为圆心，圆心角为，为半径的所对应的弧长，
点经过的路径长；
  
【问题拓展】解：连接，交于，连接，，如图所示
  
．
由旋转得，．    
在中，
．
在中，
，
，
．       
．
．
，       
在和中，
，
又，，
．
又，
，
．
【点睛】本题考查了旋转的性质，弧长公式，解直角三角形，三角形全等的性质与判定，解题的关键是抓住图形旋转前后的对应边相等，对应角相等，正确作出辅助线构造出直角三角形．
21．（2023·浙江绍兴·统考中考真题）在平行四边形中（顶点按逆时针方向排列），为锐角，且．
  
(1)如图1，求边上的高的长．
(2)是边上的一动点，点同时绕点按逆时针方向旋转得点．
①如图2，当点落在射线上时，求的长．
②当是直角三角形时，求的长．
【答案】(1)8
(2)①；②或
【分析】（1）利用正弦的定义即可求得答案；
（2）①先证明，再证明，最后利用相似三角形对应边成比例列出方程即可；
②分三种情况讨论完成，第一种：为直角顶点；第二种：为直角顶点；第三种，为直角顶点，但此种情况不成立，故最终有两个答案．
【详解】（1）在中，，
在中，．
（2）①如图1，作于点，由（1）得，，则，
作交延长线于点，则，
  
∴．
∵
∴．
由旋转知，
∴．
设，则．
∵，
∴，
∴，
∴，即，
∴，
∴．
②由旋转得，，
又因为，所以．
情况一：当以为直角顶点时，如图2．
  
∵，
∴落在线段延长线上．
∵，
∴，
由（1）知，，
∴．
情况二：当以为直角顶点时，如图3．
  
设与射线的交点为，
作于点．
∵，
∴，
∵，
∴，
∴．
又∵，
∴，
∴．
设，则，
∴
∵，
∴，
∴，
∴，
∴，
化简得，
解得，
∴．
情况三：当以为直角顶点时，
点落在的延长线上，不符合题意．
综上所述，或．
【点睛】本题考查了平行四边形的性质，正弦的定义，全等的判定及性质，相似的判定及性质，理解记忆相关定义，判定，性质是解题的关键．
22．（2023·四川南充·统考中考真题）如图，正方形中，点在边上，点是的中点，连接，．
  
(1)求证：；
(2)将绕点逆时针旋转，使点的对应点落在上，连接．当点在边上运动时（点不与，重合），判断的形状，并说明理由．
(3)在（2）的条件下，已知，当时，求的长．
【答案】(1)见解析
(2)等腰直角三角形，理由见解析
(3)
【分析】（1）根据正方形的基本性质以及“斜中半定理”等推出，即可证得结论；
（2）由旋转的性质得，从而利用等腰三角形的性质推出，再结合正方形对角线的性质推出，即可证得结论；
（3）结合已知信息推出，从而利用相似三角形的性质以及勾股定理进行计算求解即可．
【详解】（1）证：∵四边形为正方形，
∴，，
∵点是的中点，
∴，
∴，
∴，即：，
在与中，

∴，
∴；
（2）解：为等腰直角三角形，理由如下：
由旋转的性质得：，
∴，
∴，，
∵，
∴，即：，
∴，
∴，
∴，
∴，
∴为等腰直角三角形；
（3）解：如图所示，延长交于点，
∵，，
∴，，
∴，
∵，
∴，
∵，
∴，
∵，
∴，
∵，
∴，
∵，
∴，
∴，
∴，
∵，
∴，
设，则，，
∴，
解得：，（不合题意，舍去），
∴．
  
【点睛】本题考查正方形的性质，旋转的性质，全等三角形和相似三角形的判定与性质等，理解并熟练运用基本图形的证明方法和性质，掌握勾股定理等相关计算方式是解题关键．
23．（2023·江苏扬州·统考中考真题）【问题情境】
在综合实践活动课上，李老师让同桌两位同学用相同的两块含的三角板开展数学探究活动，两块三角板分别记作和，设．
【操作探究】
如图1，先将和的边、重合，再将绕着点A按顺时针方向旋转，旋转角为，旋转过程中保持不动，连接．
  
(1)当时，________；当时，________；
(2)当时，画出图形，并求两块三角板重叠部分图形的面积；
(3)如图2，取的中点F，将绕着点A旋转一周，点F的运动路径长为________．
【答案】(1)2；30或210
(2)画图见解析；
(3)
【分析】（1）当时，与重合，证明为等边三角形，得出；当时，根据勾股定理逆定理得出，两种情况讨论：当在下方时，当在上方时，分别画出图形，求出结果即可；
（2）证明四边形是正方形，得出， 求出，得出，求出，根据求出两块三角板重叠部分图形的面积即可；
（3）根据等腰三角形的性质，得出，即，确定将绕着点A旋转一周，点F在以为直径的圆上运动，求出圆的周长即可．
【详解】（1）解：∵和中，
∴，
∴当时，与重合，如图所示：连接，
  
∵，，
∴为等边三角形，
∴；
当时，
∵，
∴当时，为直角三角形，，
∴，
当在下方时，如图所示：
  
∵，
∴此时；
当在上方时，如图所示：
  
∵，
∴此时；
综上分析可知，当时，或；
故答案为：2；30或210．
（2）解：当时，如图所示：
  
∵，
∴，
∴，
∵，
又∵，
∴四边形是矩形，
∵，
∴四边形是正方形，
∴，
∴，
∴，
∵，
∴，
∴

，
即两块三角板重叠部分图形的面积为．
（3）解：∵，为的中点，
∴，
∴，
∴将绕着点A旋转一周，点F在以为直径的圆上运动，
∵
∴点F运动的路径长为．
故答案为：．
  
【点睛】本题主要考查了正方形的判定和性质，解直角三角形，旋转的性质，确定圆的条件，等腰三角形的性质，等边三角形的判定和性质，解题的关键是画出相应的图形，数形结合，并注意分类讨论．
24．（2023·湖南·统考中考真题）（1）[问题探究]
如图1，在正方形中，对角线相交于点O．在线段上任取一点P（端点除外），连接．
  
①求证：；
②将线段绕点P逆时针旋转，使点D落在的延长线上的点Q处．当点P在线段上的位置发生变化时，的大小是否发生变化？请说明理由；
③探究与的数量关系，并说明理由．
（2）[迁移探究]
如图2，将正方形换成菱形，且，其他条件不变．试探究与的数量关系，并说明理由．
  
【答案】（1）①见解析；②不变化，，理由见解析；③，理由见解析
（2），理由见解析
【分析】（1）①根据正方形的性质证明，即可得到结论；
②作，垂足分别为点M、N，如图，可得，证明四边形是矩形，推出，证明， 得出，进而可得结论；
③作交于点E，作于点F，如图，证明，即可得出结论；
（2）先证明，作交于点E，交于点G，如图，则四边形是平行四边形，可得，都是等边三角形，进一步即可证得结论．
【详解】（1）①证明：∵四边形是正方形，
∴，
∵，
∴，
∴；
②的大小不发生变化，；
证明：作，垂足分别为点M、N，如图，
  
∵四边形是正方形，
∴，，
∴四边形是矩形，，
∴，
∵，
∴，
∴，
∵，
∴，即；
③；
证明：作交于点E，作于点F，如图，
      
∵四边形是正方形，
∴，，
∴，四边形是矩形，
∴，
∴，
∵，，
∴，
作于点M，
则，
∴，
∵，
∴，
∴；
（2）；
证明：∵四边形是菱形，，
∴，
∴是等边三角形，垂直平分，
∴，
∵，
∴，
作交于点E，交于点G，如图，
则四边形是平行四边形，，，
∴，都是等边三角形，
∴，
    
作于点M，则，
∴，
∴．
【点睛】本题是四边形综合题，主要考查了正方形、菱形的性质，矩形、平行四边形、等边三角形的判定和性质，全等三角形的判定和性质以及解直角三角形等知识，熟练掌握相关图形的判定和性质、正确添加辅助线是解题的关键．
25．（2023·湖北随州·统考中考真题）1643年，法国数学家费马曾提出一个著名的几何问题：给定不在同一条直线上的三个点A，B，C，求平面上到这三个点的距离之和最小的点的位置，意大利数学家和物理学家托里拆利给出了分析和证明，该点也被称为“费马点”或“托里拆利点”，该问题也被称为“将军巡营”问题．
(1)下面是该问题的一种常见的解决方法，请补充以下推理过程：（其中①处从“直角”和“等边”中选择填空，②处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空，③处填写角度数，④处填写该三角形的某个顶点）
当的三个内角均小于时，
如图1，将绕，点C顺时针旋转得到，连接，
    
由，可知为 ① 三角形，故，又，故，
由 ② 可知，当B，P，，A在同一条直线上时，取最小值，如图2，最小值为，此时的P点为该三角形的“费马点”，且有 ③ ；
已知当有一个内角大于或等于时，“费马点”为该三角形的某个顶点．如图3，若，则该三角形的“费马点”为 ④ 点．
(2)如图4，在中，三个内角均小于，且，已知点P为的“费马点”，求的值；
  
(3)如图5，设村庄A，B，C的连线构成一个三角形，且已知．现欲建一中转站P沿直线向A，B，C三个村庄铺设电缆，已知由中转站P到村庄A，B，C的铺设成本分别为a元/，a元/，元/，选取合适的P的位置，可以使总的铺设成本最低为___________元．（结果用含a的式子表示）
【答案】(1)①等边；②两点之间线段最短；③；④A．
(2)
(3)
【分析】（1）根据旋转的性质和两点之间线段最短进行推理分析即可得出结论；
（2）根据（1）的方法将绕，点C顺时针旋转得到，即可得出可知当B，P，，A在同一条直线上时，取最小值，最小值为，在根据可证明，由勾股定理求即可，
（3）由总的铺设成本，通过将绕，点C顺时针旋转得到，得到等腰直角，得到，即可得出当B，P，，A在同一条直线上时，取最小值，即取最小值为，然后根据已知和旋转性质求出即可．
【详解】（1）解：∵，
∴为等边三角形；
∴，，
又，故，
由两点之间线段最短可知，当B，P，，A在同一条直线上时，取最小值，
最小值为，此时的P点为该三角形的“费马点”，
∴，，
∴，，
又∵，
∴，
∴，
∴；
∵，
∴，，
∴，，
∴三个顶点中，顶点A到另外两个顶点的距离和最小．
又∵已知当有一个内角大于或等于时，“费马点”为该三角形的某个顶点．
∴该三角形的“费马点”为点A，
故答案为：①等边；②两点之间线段最短；③；④．
（2）将绕，点C顺时针旋转得到，连接，
由（1）可知当B，P，，A在同一条直线上时，取最小值，最小值为，
  
∵，
∴，
又∵
∴，
由旋转性质可知：，
∴，
∴最小值为，
（3）∵总的铺设成本
∴当最小时，总的铺设成本最低，
将绕，点C顺时针旋转得到，连接，
由旋转性质可知：，，，，
∴，
∴，
当B，P，，A在同一条直线上时，取最小值，即取最小值为，
  
过点作，垂足为，
∵，，
∴，
∴，
∴，
∴，
∴
的最小值为
总的铺设成本（元）
故答案为：
【点睛】本题考查了费马点求最值问题，涉及到的知识点有旋转的性质，等边三角形的判定与性质，勾股定理，以及两点之间线段最短等知识点，读懂题意，利用旋转作出正确的辅助线是解本题的关键．
26．（2023·四川·统考中考真题）如图1，已知线段，，线段绕点在直线上方旋转，连接，以为边在上方作，且．
  
(1)若，以为边在上方作，且，，连接，用等式表示线段与的数量关系是 　 　；
(2)如图2，在(1)的条件下，若，，，求的长；
(3)如图3，若，，，当的值最大时，求此时的值．
【答案】(1)
(2)
(3)
【分析】（1）在中，，，且，，可得，根据相似三角形的性质得出，，进而证明，根据相似三角形的性质即可求解；
（2）延长交于点，如图所示，在中，求得，进而求得的长，根据（1）的结论，得出，在中，勾股定理求得，进而根据，即可求解．
（3）如图所示，以为边在上方作，且，，连接，，，同（1）可得，进而得出在以为圆心，为半径的圆上运动，当点三点共线时，的值最大，进而求得，，根据得出，过点作，于点，分别求得,然后求得，最后根据正切的定义即可求解．
【详解】（1）解：在中，，，且，，
∴，，
∴，，
∴
∴
∴，
故答案为：．
（2）∵，且，，
∴，，
延长交于点，如图所示，
  
∵，
∴，
∴在中，，，
∴，
由（1）可得，
∴，
∴，
在中，，
∵，
∴，
∴，
∴；
（3）解：如图所示，以为边在上方作，且，，连接，，，
  
同（1）可得
则，
∵，则，
在中，，，
∴在以为圆心，为半径的圆上运动，
∴当点三点共线时，的值最大，此时如图所示，则，
  
在中，
∴,，
∵，
∴，
过点作，于点，
∴，，
∵，
∴，
∴，
中，．
【点睛】本题考查了相似三角形的性质与判定，勾股定理，解直角三角形，正切的定义，求圆外一点到圆的距离的最值问题，熟练掌握相似三角形的性质与判定是解题的关键．



27．（2023·湖北黄冈·统考中考真题）【问题呈现】
和都是直角三角形，，连接，，探究，的位置关系．
  
(1)如图1，当时，直接写出，的位置关系：____________；
(2)如图2，当时，（1）中的结论是否成立？若成立，给出证明；若不成立，说明理由．
【拓展应用】
(3)当时，将绕点C旋转，使三点恰好在同一直线上，求的长．
【答案】(1)
(2)成立；理由见解析
(3)或

【分析】（1）根据，得出，，证明，得出，根据，求出，即可证明结论；
（2）证明，得出，根据，求出，即可证明结论；
（3）分两种情况，当点E在线段上时，当点D在线段上时，分别画出图形，根据勾股定理求出结果即可．
【详解】（1）解：∵，
∴，，
∵，
∴，
∴，
∴，
∴，
∵，



，
∴，
∴；
故答案为：．
  
（2）解：成立；理由如下：
∵，
∴，
∴，
∵，
∴，
∴，
∵，



，
∴，
∴；
  
（3）解：当点E在线段上时，连接，如图所示：
  
设，则，
根据解析（2）可知，，
∴，
∴，
根据解析（2）可知，，
∴，
根据勾股定理得：，
即，
解得：或（舍去），
∴此时；
当点D在线段上时，连接，如图所示：
  
设，则，
根据解析（2）可知，，
∴，
∴，
根据解析（2）可知，，
∴，
根据勾股定理得：，
即，
解得：或（舍去），
∴此时；
综上分析可知，或．
【点睛】本题主要考查了全等三角形的判定和性质，相似三角形的判定和性质，三角形内角和定理的应用，勾股定理，解题的关键是熟练掌握三角形相似的判定方法，画出相应的图形，注意分类讨论．
28．（2023·内蒙古赤峰·统考中考真题）数学兴趣小组探究了以下几何图形．如图①，把一个含有角的三角尺放在正方形中，使角的顶点始终与正方形的顶点重合，绕点旋转三角尺时，角的两边，始终与正方形的边，所在直线分别相交于点，，连接，可得．
  
【探究一】如图②，把绕点C逆时针旋转得到，同时得到点在直线上．求证：；
【探究二】在图②中，连接，分别交，于点，．求证：；
【探究三】把三角尺旋转到如图③所示位置，直线与三角尺角两边，分别交于点，．连接交于点，求的值．
【答案】[探究一]见解析；[探究二]见解析；[探究三]
【分析】[探究一]证明，即可得证；
[探究二]根据正方形的性质证明，根据三角形内角和得出，加上公共角，进而即可证明
[探究三]先证明，得出，，将绕点顺时针旋转得到，则点在直线上．得出，根据全等三角形的性质得出，进而可得，证明，根据相似三角形的性质得出，即可得出结论．
【详解】[探究一]
∵把绕点C逆时针旋转得到，同时得到点在直线上，
∴，
∴，
∴，
在与中

∴
∴
[探究二]证明：如图所示，
  
∵四边形是正方形，
∴，
又，
∴，
∵，
∴，
又∵，
∴，
又∵公共角，
∴；
[探究三] 证明：∵是正方形的对角线，
∴，，
∴，
∵，
∴，
即，
∴，
∴，，
如图所示，将绕点顺时针旋转得到，则点在直线上．
  
∴，，
∴，
又，
∴，
∴，
∵，
∴，
又，
∴，
∴，
即．
【点睛】本题考查了全等三角形的性质与判定，旋转的性质，正方形的性质，相似三角形的性质与判定，熟练掌握相似三角形的性质与判定是解题的关键．

29．（2023·湖南·统考中考真题）问题情境：小红同学在学习了正方形的知识后，进一步进行以下探究活动：在正方形的边上任意取一点G，以为边长向外作正方形，将正方形绕点B顺时针旋转．
    
特例感知：
（1）当在上时，连接相交于点P，小红发现点P恰为的中点，如图①．针对小红发现的结论，请给出证明；
（2）小红继续连接，并延长与相交，发现交点恰好也是中点P，如图②，根据小红发现的结论，请判断的形状，并说明理由；
规律探究：
（3）如图③，将正方形绕点B顺时针旋转，连接，点P是中点，连接，，，的形状是否发生改变？请说明理由．
【答案】（1）见解析；（2）是等腰直角三角形，理由见解析；（3）的形状不改变，见解析
【分析】（1）连接，，，根据正方形的性质求出，证明，推出，再利用余角的性质求出，推出即可；
（2）根据正方形的性质直接得到，推出，得到是等腰直角三角形；
（3）延长至点M，使，连接，证明，得到，推出，设交于点H，交于点N，得到，由得到，推出，进而得到，再证明，得到，，证得，再由，根据等腰三角形的三线合一的性质求出，即可证得是等腰直角三角形．
【详解】（1）证明：连接，，，如图，
  
∵四边形，都是正方形，
∴，
∴，
∵四边形是正方形，
∴，
又∵，
∴，
∴，
∴，
∵，
∴，
∴，
∴，即点P恰为的中点；
（2）是等腰直角三角形，理由如下：
∵四边形，都是正方形，
∴
∴，
∴是等腰直角三角形；
（3）的形状不改变，
延长至点M，使，连接，
  
∵四边形、四边形都是正方形，
∴，，
∵点P为的中点，
∴，
∵，
∴，
∴，
∴，，
∴，
设交于点H，交于点N，
∴，
∵，
∴，
∵，
∴，
∵，
∴，
又∵，
∴，
∴，，
∵，
∴，即，
∵，
∴，即，
∴，
∴，
∴，
∴是等腰直角三角形．
【点睛】此题考查了正方形的性质，全等三角形的判定和性质，等腰直角三角形的判定和性质，平行线的性质等，（3）中作辅助线利用中点构造全等三角形是解题的难点，熟练掌握各性质和判定定理是解题的关键．
30．（2023·贵州·统考中考真题）如图①，小红在学习了三角形相关知识后，对等腰直角三角形进行了探究，在等腰直角三角形中，，过点作射线，垂足为，点在上．
  
(1)【动手操作】
如图②，若点在线段上，画出射线，并将射线绕点逆时针旋转与交于点，根据题意在图中画出图形，图中的度数为_______度；
(2)【问题探究】
根据（1）所画图形，探究线段与的数量关系，并说明理由；
(3)【拓展延伸】
如图③，若点在射线上移动，将射线绕点逆时针旋转与交于点，探究线段之间的数量关系，并说明理由．
【答案】(1)作图见解析；135
(2)；理由见解析
(3)或；理由见解析
【分析】（1）根据题意画图即可；先求出，根据，求出；
（2）根据，，证明、P、B、E四点共圆，得出，求出，根据等腰三角形的判定即可得出结论；
（3）分两种情况，当点P在线段上时，当点P在线段延长线上时，分别画出图形，求出之间的数量关系即可．
【详解】（1）解：如图所示：
  
∵，
∴，
∵，
∴，
∴；
故答案为：135．
（2）解：；理由如下：
连接，如图所示：
  
根据旋转可知，，
∵，
∴、P、B、E四点共圆，
∴，
∴，
∴，
∴．
（3）解：当点P在线段上时，连接，延长，作于点F，如图所示：
  
根据解析（2）可知，，
∵，
∴，
∴，
∵，
∴，
∴，
∵，，
∴为等腰直角三角形，
∴，
∵为等腰直角三角形，
∴，
即；
当点P在线段延长线上时，连接，作于点F，如图所示：
  
根据旋转可知，，
∵，
∴、B、P、E四点共圆，
∴，
∴，
∴，
∴，
∵，
∴，
∴，
∵，
∴，
∴，
∵，
∴，
∵，，
∴为等腰直角三角形，
∴，
即；
综上分析可知，或．
【点睛】本题主要考查了等腰三角形的判定和性质，三角形全等的判定和性质，圆周角定理，四点共圆，等腰直角三角形的性质，解题的关键是作出图形和相关的辅助线，数形结合，并注意分类讨论．