

2022-2023学年广东省广州市南沙区八年级(下)期末数学试卷(含解析)
展开这是一份2022-2023学年广东省广州市南沙区八年级(下)期末数学试卷(含解析),共19页。试卷主要包含了选择题,解答题等内容,欢迎下载使用。
2022-2023学年广东省广州市南沙区八年级(下)期末数学试卷
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列式子中,为最简二次根式的是( )
A. 12 B. 3 C. 4 D. 12
2. 下列各组数中,不能构成直角三角形的一组是( )
A. 5,7,10 B. 3,4,5 C. 6,8,10 D. 1,2, 3
3. 在四边形ABCD中,AB//DC,当满足下列哪个条件时,可以得出四边形ABCD是平行四边形( )
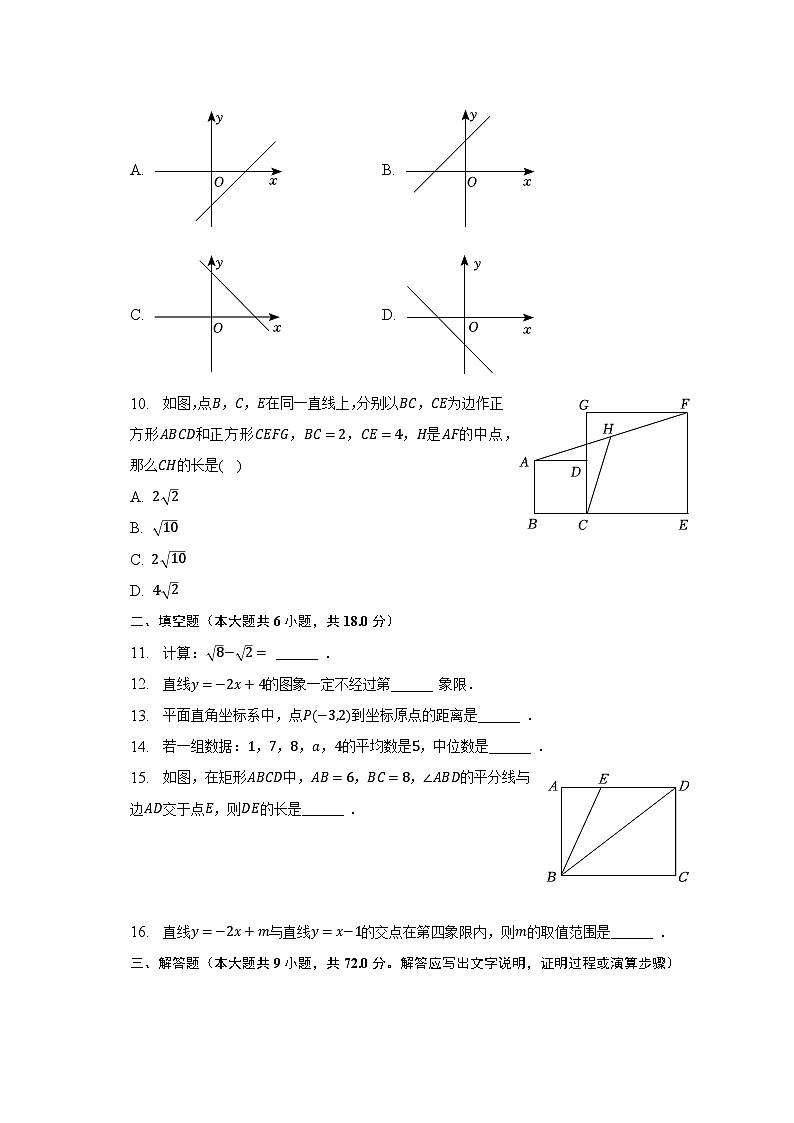
A. ∠A+∠C=180° B. ∠B+∠D=180°
C. ∠A+∠B=180° D. ∠A+∠D=180°
4. 已知函数y=(k−3)x是正比例函数,且y随着x的增大而减小,则下面判断正确的是( )
A. k>0 B. k<0 C. k>3 D. k<3
5. 若甲、乙、丙、丁四位同学在八年级第一学期4次数学测试的平均成绩恰好都是85分,方差分别为S甲2=0.80,S乙2=1.75,S丙2=0.32,S丁2=1.26,则成绩最稳定的同学是( )
A. 甲 B. 乙 C. 丙 D. 丁
6. 菱形ABCD的对角线AC=4,∠D=60°,则对角线BD的长是( )
A. 4 3 B. 2 3 C. 4 D. 2
7. 如图,一个工人拿一个2.5米长的梯子,底端A放在距离墙根C点0.7米处,另一头B点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑多少米?( )
A. 0.4 B. 0.6 C. 0.7 D. 0.8
8. 如果 (2a−1)2=2a−1,且a是非负数,则( )
A. 0
A. B.
C. D.
10. 如图,点B,C,E在同一直线上,分别以BC,CE为边作正方形ABCD和正方形CEFG,BC=2,CE=4,H是AF的中点,那么CH的长是( )
A. 2 2
B. 10
C. 2 10
D. 4 2
二、填空题(本大题共6小题,共18.0分)
11. 计算: 8− 2= ______ .
12. 直线y=−2x+4的图象一定不经过第______ 象限.
13. 平面直角坐标系中,点P(−3,2)到坐标原点的距离是______ .
14. 若一组数据:1,7,8,a,4的平均数是5,中位数是______ .
15. 如图,在矩形ABCD中,AB=6,BC=8,∠ABD的平分线与边AD交于点E,则DE的长是______ .
16. 直线y=−2x+m与直线y=x−1的交点在第四象限内,则m的取值范围是______ .
三、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
17. (本小题4.0分)
计算: 3( 12+1).
18. (本小题4.0分)
如图,在△ABC中,∠A=55°,∠C=35°,AC=4,BC=3.求AB的长.
19. (本小题6.0分)
周长为20cm的矩形,若它的一边长是x cm,面积是S cm2.
(1)请用含x的式子表示S,并指出常量与变量;
(2)当x=6时,求S的值.
20. (本小题6.0分)
如图,AE//BF,∠BAE的平分线交BF于点C,点D在AE上,AB=AD,连接CD.
求证:四边形ABCD是菱形.
21. (本小题8.0分)
请阅读下面的材料,并探索用材料中的方法解决问题.
【材料1】两个含有二次根式而非零的代数式相乘,如果它们的积不含二次根式,那么这两个代数式互为有理化因式.
例如:( 3+ 2)( 3− 2)=1,我们称 3+ 2的一个有理化因式是 3− 2.
【材料2】如果一个代数式的分母中含有二次根式,通常可将分子、分母同乘分母的有理化因式,使分母中不含根号,这种变形叫做分母有理化.
例如:2 3+ 2=2( 3− 2)( 3+ 2)( 3− 2)=2( 3− 2)1=2 3−2 2.
问题探究:(1)写出 5− 7的一个有理化因式:______ ;
(2)计算:(2 3+3 2)(2 3−3 2)−( 3+ 2)2;
(3)将式子222 5+3分母有理化.
22. (本小题10.0分)
某渔业养殖户在自家鱼塘中放养了某种鱼2000条,若干年后,准备打捞出售,为了估计鱼塘中这种鱼的总质量,现从鱼塘中捕捞三次,得到数据如下表:
鱼的条数(条)
平均每条鱼的质量(千克)
第一次
30
2.8
第二次
40
3
第三次
30
3.2
(1)求鱼塘中这种鱼平均每条的重量.
(2)若这种鱼放养的成活率是85%,请估计鱼塘中这种鱼的总重量.(新生鱼和死鱼不计算入内.)
(3)如果把鱼塘中放养的2000条中存活的这种鱼全部卖掉,价格为每千克20元,若投资成本为45000元,求卖出后获得的纯利润.
23. (本小题10.0分)
一次函数y=kx+2的图象与x轴交于点A,与y轴交于点C.一次函数y=−x+4的图象与x轴交于点B,与y轴交于点D.两函数图象交于点P(m,3).
(1)求k和m的值;
(2)求线段AP的长;
(3)若直线AC上有一动点Q,过Q作直线QH,QH平行于y轴,QH直线BD于点H.当QH=OB时,求Q的坐标.
24. (本小题12.0分)
如图,在△ABC中,∠ACB=90°,AC=6cm,AB=10cm.动点P从点A出发,沿着A→C→B→A的路径,以每秒2cm的速度运动,当P回到A点时运动结束,设点P运动的时间为t秒.
(1)当t=2时,求△BPC的面积;
(2)若AP平分∠CAB,求t的值;
(3)深入探索:若点P运动到边AB,且△ACP是等腰三角形,求t的值.
25. (本小题12.0分)
已知,如图①,在▱ABCD中,∠A=90°,AB=BC=4 5,点E为CD上的一动点,连接BE,过点C作CH⊥BE于点H,以CH为腰作等腰直角△HCG,∠HCG=90°,连接DH.
(1)求证:四边形ABCD为正方形;
(2)如图②,当D,H,G三点共线时,求DH2+DG2的值;
(3)求DH的最小值.
答案和解析
1.【答案】B
【解析】解:A. 12= 22,所以A选项不符合题意;
B. 3为最简二次根式,所以B选项符合题意;
C. 4=2,所以C选项不符合题意;
D. 12=2 3,所以D选项不符合题意;
故选:B.
根据最简二次根式的定义对各选项进行判断.
本题考查了最简二次根式:掌握最简二次根式满足的条件(被开方数不含分母;被开方数中不含能开得尽方的因数或因式)是解决问题的关键.
2.【答案】A
【解析】解:A、52+72≠102,不能构成直角三角形,故本选项符合题意;
B、32+42=52,能构成直角三角形,故本选项不符合题意;
C、62+82=102,能构成直角三角形,故本选项不符合题意;
D、12+( 3)2=22,能构成直角三角形,故本选项不符合题意.
故选:A.
根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个三角形是直角三角形.如果没有这种关系,这个就不是直角三角形.
本题考查了勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.
3.【答案】D
【解析】解:∠A+∠C=180°与∠B+∠D=180°以及∠B+∠C=180°,都不能判定AD//BC或者AB=CD.故A、B、C不符合题意.
若∠A+∠B=180°时,AD//BC,所以根据“有两组对边互相平行的四边形是平行四边形”可以判定四边形ABCD是平行四边形,选项D符合题意.
故选:D.
平行四边形的五种判定方法分别是:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形;(5)对角线互相平分的四边形是平行四边形.根据平行四边形的判定逐一验证.
本题考查平行四边形的判定,对于判定定理:“一组对边平行且相等的四边形是平行四边形.”应用时要注意必须是“一组”,而“一组对边平行且另一组对边相等”的四边形不一定是平行四边形.
4.【答案】D
【解析】解:∵函数y=(k−3)x是正比例函数,且y随着x的增大而减小,
∴k−3<0,
解得k<3.
故选:D.
根据正比例函数y=(k−3)x中,y随着x增大而减小得出关于k的不等式,求出k的取值范围即可.
本题考查的是一次函数图象与系数的关系,掌握正比例函数y=kx(k≠0)中,当k<0时,y随x的增大而减小是解题的关键.
5.【答案】C
【解析】解:∵S甲2=0.80,S乙2=1.75,S丙2=0.32,S丁2=1.26,
∴S丙2
故选:C.
根据方差的定义,方差越小数据越稳定,即可得出答案.
本题主要考查方差,解题的关键是掌握方差的意义:方差是反映一组数据的波动大小的一个量.方差越大,则它与平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
6.【答案】A
【解析】解:∵四边形ABCD是菱形,
∴AC⊥BD,AO=OC,BD=2OD,∠ADO=12∠ADC,
∵∠ADC=60°,
∴∠ADO=30°,
∵AC=4,
∴AO=12AC=2,
∴OD= 3AO=2 3,
∴BD=4 3.
故选:A.
由菱形的性质,推出AC⊥BD,AO=OC,BD=2OD,∠ADO=12∠ADC,得到∠ADO=30°,AO=12AC=2,由直角三角形的性质求出OD= 3AO=2 3,得到BD=4 3.
本题考查菱形的性质,直角三角形的性质,关键是由菱形的性质求出∠ADO=30°,AO=2,由直角三角形的性质即可解决问题.
7.【答案】D
【解析】解:∵AB=2.5米,AC=0.7米,
∴BC= AB2−AC2=2.4(米),
∵梯子的顶部下滑0.4米,
∴BE=0.4米,
∴EC=BC−0.4=2米,
∴DC= DE2−EC2=1.5米.
∴梯子的底部向外滑出AD=1.5−0.7=0.8(米).
故选:D.
首先在直角三角形ABC中计算出CB长,再由题意可得EC长,再次在直角三角形EDC中计算出DC长,从而可得AD的长度.
此题主要考查了勾股定理在实际生活中的应用,关键是掌握直角三角形中,两直角边的平方和等于斜边的平方.
8.【答案】C
【解析】解:∵ (2a−1)2=|2a−1|=2a−1,
∴2a−1≥0,
即a≥12,
故选:C.
根据二次根式的性质与化简方法进行计算即可.
本题考查二次根式的性质与化简,理解负数没有平方根,即二次根式的被开方数为非负数是正确解答的关键.
9.【答案】D
【解析】解:∵正比例函数y=kx的图象在第二、第四象限,
∴k<0,
∵常数k和b互为相反数,
∴b>0,
∴一次函数y=kx−b在平面直角坐标系中的图象在第二、三、四象限,
故选:D.
根据正比例函数的性质确定k的符号,然后根据一次函数的性质即可得到结论.
本题考查了正比例函数的性质,一次函数的性质,熟练掌握正比例函数和一次函数的性质是解题的关键.
10.【答案】B
【解析】解:连接AC、CF,
在正方形ABCD和正方形CEFG中,
∠ACG=45°,∠FCG=45°,
∴∠ACF=90°,
∵BC=2,CE=4,
∴AC=2 2,CF=4 2,
由勾股定理得,AF=2 10,又H是AF的中点,
∴CH=12AF= 10,
故选:B.
连接AC、CF,根据正方形的性质得到∠ACF=90°,根据勾股定理求出AF的长,根据直角三角形中,斜边上的中线等于斜边的一半计算即可.
本题考查的是直角三角形的性质、勾股定理的应用、正方形的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.
11.【答案】 2
【解析】解: 8− 2
=2 2− 2
= 2.
故答案为: 2.
利用二次根式的减法的法则进行运算即可.
本题主要考查二次根式的加减法,解答的关键是对相应的运算法则的掌握.
12.【答案】三
【解析】解:∵直线y=−2x+4中,k=−2,b=4,
∴此直线经过一、二、四象限,不经过第三象限.
故答案为:三.
先根据一次函数的解析式判断出k、b的值,再根据一次函数的图象与系数的关系即可得出结论.
本题考查的是一次函数的图象与系数的关系,即一次函数y=kx+b(k≠0)中,当k<0,b>0⇔y=kx+b的图象在一、二、四象限.
13.【答案】 13
【解析】解:∵点P(−3,2)
∴点P(−3,2)到坐标原点的距离= (−3)2+22= 13,
故答案为: 13.
根据勾股定理即可得到结论.
本题考查了勾股定理,熟练掌握勾股定理是解题的关键.
14.【答案】5
【解析】解:∵1,7,8,a,4的平均数是5,
∴a=25−1−7−8−4=5,
因此这组数据为:1,7,8,5,4,
将这5个数据从小到大排列,处在中间位置的一个数是5,
所以中位数是5,
故答案为:5.
根据平均数的计算方法求出a,再根据中位数的定义进行计算即可.
本题考查平均数、中位数,掌握平均数的计算方法,中位数的定义是正确解答的关键.
15.【答案】5
【解析】解:过E作EH⊥BD于H,
∵四边形ABCD是矩形,
∴∠A=90°,AD=BC=8,
∴BD= AB2+AD2=10,
∵BE平分∠ABD,
∴AE=EH,
在Rt△ABE与Rt△HBE中,
AE=EHBE=BE,
∴Rt△ABE≌Rt△HBE(HL),
∴BH=AB=6,
∴DH=10−6=4,
∵DE2=EH2+DH2,
∴DE2=(8−DE)2+42,
解得DE=5,
故答案为:5.
过E作EH⊥BD于H,根据勾股定理得到BD= AB2+AD2=10,根据角平分线的性质得到AE=EH,根据全等三角形的性质得到BH=AB=6,根据勾股定理即可得到结论.
本题考查了矩形的性质,全等三角形 的判定和性质,勾股定理,角平分线的性质,熟练掌握矩形的性质是解题的关键.
16.【答案】−1
解得x=m+13y=m−23,
∵交点在第四象限,
∴m+13>0m−23<0,
解得−1
本题考查了两直线相交的问题,解一元一次不等式组,联立两函数解析式求交点坐标是常用的方法,要熟练掌握并灵活运用.
17.【答案】解: 3( 12+1)
= 3× 12+ 3×1
=6+ 3.
【解析】利用二次根式的乘法的法则进行运算即可.
本题主要考查二次根式的混合运算,解答的关键是对相应的运算法则的掌握.
18.【答案】解:∵∠A=55°,∠C=35°,
∴∠B=180°−∠A−∠C=180°−55°−35°=90°.
故△ABC为直角三角形,
∴AB= AC2−BC2= 42−32= 7,
故AB的长为 7.
【解析】根据直角三角形勾股定理AB= AC2−BC2解.
本题考查直角三角形的勾股定理,解题的关键是先解出直角三角形,对勾股定理的熟练运用.
19.【答案】解:(1)S=x×20−2x2=−x2+10x,
周长20cm是常量;一边x cm,面积Scm2是变量.
(2)当x=6时,
S=−x2+10x
=−62+10×6
=−36+60
=24.
【解析】(1)根据函数的定义来确定常量与变量;根据矩形的面积公式写出S与x之间的关系式;
(2)代入数值求S的值.
本题考查了二次函数的定义,二次函数的解析式,函数值,解题的关键是列函数的解析式.
20.【答案】证明:∵AE//BF,
∴∠DAC=∠ACB,
∵AC平分∠BAE,
∴∠DAC=∠BAC,
∴∠ACB=∠BAC,
∴AB=BC,
∵AB=AD,
∴AD=BC,
∴四边形ABCD是菱形.
【解析】根据平行线的性质得到∠DAC=∠ACB,根据角平分线的定义得到∠DAC=∠BAC,等量代换得到∠ACB=∠BAC,根据菱形的判定定理即可得到结论.
本题考查了菱形的判定,平行线的性质,熟练掌握菱形的判定定理是解题的关键.
21.【答案】 5+ 7(答案不唯一)
【解析】解:(1)写出 5− 7的一个有理化因式: 5+ 7,
故答案为: 5+ 7(答案不唯一);
(2)(2 3+3 2)(2 3−3 2)−( 3+ 2)2
=(2 3)2−(3 2)2−(5+2 6)
=12−18−5−2 6
=−11−2 6;
(3)222 5+3=22(2 5−3)(2 5+3)(2 5−3)=22(2 5−3)11=2(2 5−3)=4 5−6.
(1)根据互为有理化因式的定义,即可解答;
(2)利用完全平方公式,平方差公式进行计算,即可解答;
(3)根据材料2的解题思路进行计算,即可解答.
本题考查了二次根式的混合运算,分母有理数,完全平方公式,平方差公式,准确熟练地进行计算是解题的关键.
22.【答案】解:(1)平均重量为:30×2.8+40×3+30×3.230+40+30=3(千克),
答:鱼塘中这种鱼平均每条的重量为3千克;
(2)∵鱼放养的成活率是85%,
∴该鱼塘中共有鱼2000×85%=1700条,
总重量为:1700×3=5100(千克),
答:估计鱼塘中这种鱼的总重量为5100千克;
(3)总收入为:5100×20=102000(元),
∴102000−45000=57000(元),
答:卖出后获得的纯利润为57000元.
【解析】(1)用加权平均数的计算方法求得鱼的平均重量即可;
(2)用总条数乘以成活率求得鱼的总条数,然后乘以平均重量即可求得总重量;
(3)算出总售价减去投资成本即可求得纯收入.
本题考查了用样本估计总体的知识,与实际生活联系非常密切,锻炼了学生们应用数学知识解决生活实际问题的能力.
23.【答案】解:(1)把P(m,3)代入一次函数y=−x+4中得3=−m+4,
∴m=1,
∴P(1,3),
把P(1,3)代入一次函数y=kx+2中得3=k+2,
∴k=1;
(2)由(1)知y=x+2,
当y=0时,x=−2,
∴A(−2,0),
∴AP= (1+2)2+32=3 2;
(3)由(1)得y=x+2,令y=0,得y=−x+4=0,
∴x=4,
∴OB=4,
设Q(t,t+2),则H(t,−t+4),
∵QH=OB,
∴|−t+4−(t+2)|=4,
∴|−t+1|=2,
解得t=3或t=−1,
当t=3时,t+2=5,
当t=−1时,t+2=1,
∴Q的坐标为(3,5)或(−1,1).
【解析】(1)把P(m,3)代入一次函数y=−x+4中求出m,根据待定系数法即可求出k;
(2)根据两点间的距离公式即可求出AP;
(3)设Q(t,t+2),则H(t,−t+4),由QH=OB,得到|−t+4−(t+2)|=4,解方程求出t,即可求出Q的坐标.
本题是一次函数的综合题,考查了待定系数法求函数的解析式,两点间的距离,分类讨论是解题的关键.
24.【答案】解:(1)如图1,在△ABC中,∠ACB=90°,AC=6cm,AB=10cm,
∴BC= AB2−AC2= 102−62=8(cm),
由题意得,当t=2时,AP=2t=4(cm),则CP=6−4=2(cm),
∴S△BPC=12×BC×CP=12×8×2=8(cm2);
(2)当线段AP恰好平分∠CAB时,作PD⊥AB于D,如图2,
∵线段AP平分∠CAB,∠ACB=90°,PD⊥AB,
∴PC=PD,AC=AD=6(cm),
∴BD=AB−AD=4(cm),
在Rt△BPD中,PB2=PD2+BD2,即(8−PC)2=PC2+42,
解得,PC=3(cm),
∴t=12(AC+PC)=12×(6+3)=4.5(s),
∴当t=4.5s时,线段AP恰好平分∠CAB;
(3)如图3,当PA=PC时,∠PAC=∠PCA,
∵∠PAC+∠B=90°,∠ACP+∠PCB=90°,
∴∠PCB=∠PBC,
∴PA=PC=PB=5cm,
∴t=12(AC+CB+BP)=9.5(s);
如图4,当AC=CP时,作CD⊥AB于点D,
△ABC的面积=12×AC×BC=12×AB×CD,即12×6×8=12×10×CD,
解得,CD=4.8,
在Rt△ACD中,AD= AC2−CD2= 62−4.82=3.6(cm),
∴AP=2AD=7.2(cm),
∴BP=AB−AP=2.8(cm),
∴t=12(AC+CB+BP)=8.4(s);
如图5,当AC=AP时,AP=6cm,AB=10cm,
∴PB=AB−AP=4cm,
∴t=12(AC+CB+BP)=9(s);
综上所述,当t为9.5s或9s或8.4s时,△ACP是等腰三角形.
【解析】(1)根据题意求出CP,根据三角形面积公式计算;
(2)作PD⊥AB于D,根据角平分线的性质得到PC=PD,根据勾股定理列式计算;
(3)分PA=PC、AC=CP、AC=AP三种情况,根据等腰三角形的性质解答.
本题考查的是勾股定理,等腰三角形的性质,灵活运用分情况讨论思想、掌握勾股定理和等腰三角形的性质定理是解题的关键.
25.【答案】(1)证明:∵四边形ABCD是平行四边形,∠A=90°,
∴四边形ABCD是矩形,
又∵AB=BC,
∴四边形ABCD是正方形.
(2)解:连接BD,BG.
∵∠BCG+∠BCH=90°,
∴∠DCH+∠BCH=90°,
∴∠BCG=∠DCH,
∵CG=CH,BC=DC,
∴△BGC≌△DHC(SAS),
∴BG=DH,∠BGC=∠DHC,
∵∠HCG=45°,
∴∠DHC=135°,
∴∠BGC=135°,
∵∠HGC=45°,
∴∠BGD=90°,
在Rt△BGD中,BG2+DG2=BD2=2AB2=160,
∵BG=DH,
∴DH2+DG2=160.
(3)解:∵∠BHC=90°,
∴点H在以BC的中点O为圆心,以2 5为半径的圆上运动.
∴DH≥OD−OH= DC2+OC2−2 5=10−2 5,
∴DH的最小值10−2 5.
【解析】(1)先证是矩形,再证是正方形;
(2)从DH2+DG2形式看,联想到勾股定理,说明三角形DHG是直角三角形即可;
(3)D,H两点一定一动,由CH⊥BE联想到隐圆.
此题以正方形为载体,考查了正方形的判断,三角形全等,隐圆及线段的最值,综合性强.
相关试卷
这是一份2023-2024学年广东省广州市南沙区七年级(上)期末数学试卷(含解析),共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2022-2023学年广东省广州市南沙区八年级(下)期末数学试卷(含解析),共19页。试卷主要包含了选择题,解答题等内容,欢迎下载使用。
这是一份2022-2023学年广东省广州市南沙区八年级(下)期末数学试卷,共18页。试卷主要包含了选择题,解答题等内容,欢迎下载使用。












