2022-2023学年湖北省十堰市郧西县八年级（下）期末数学试卷（含解析）

这是一份2022-2023学年湖北省十堰市郧西县八年级（下）期末数学试卷（含解析），共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年湖北省十堰市郧西县八年级（下）期末数学试卷
一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）
1. 式子 x−2在实数范围内有意义，则x的取值范围是(    )
A. x≥0 B. x≤2 C. x≥−2 D. x≥2
2. 在平面直角坐标系中，点P(3,4)到原点的距离是(    )
A. 3 B. 4 C. 5 D. 7
3. 在平面直角坐标系xOy中，函数y=2x−1的图象经过(    )
A. 第一、二、三象限 B. 第一、二、四象限 C. 第二，三、四象限 D. 第一、三、四象限
4. 矩形和菱形都具有的性质是(    )
A. 对角线相等 B. 对角线互相平分 C. 对角线互相垂直 D. 邻边相等
5. 一家鞋店在一段时间内销售了某种女鞋30双，各种尺码鞋的销售量如表：
尺码/cm
22
22.5
23
23.5
24
24.5
25
销售量(双)
1
2
5
11
7
3
1
鞋店老板决定下次进货多进23.5cm的鞋，可用来解释这一现象的统计量是(    )
A. 平均数 B. 中位数 C. 众数 D. 方差
6. 一次函数y=ax+b(a,b是常数，且a≠0)，若2a+b+3=0，则这个一次函数的图象必经的点是(    )
A. (−1,−5) B. (2,−3) C. (32,0) D. (1,2)
7. 下列条件中，不能判定△ABC是直角三角形的是(    )
A. ∠A=∠B+∠C B. a：b：c=3：4：5
C. a2=(b+c)(b−c) D. ∠A：∠B：∠C=1：1：4
8. 如图，在平行四边形ABCD中，已知AD=5cm，AB=3cm，AE平分∠BAD交BC边于点E，则EC等于(    )
A. 1cm
B. 2cm
C. 3cm
D. 4cm
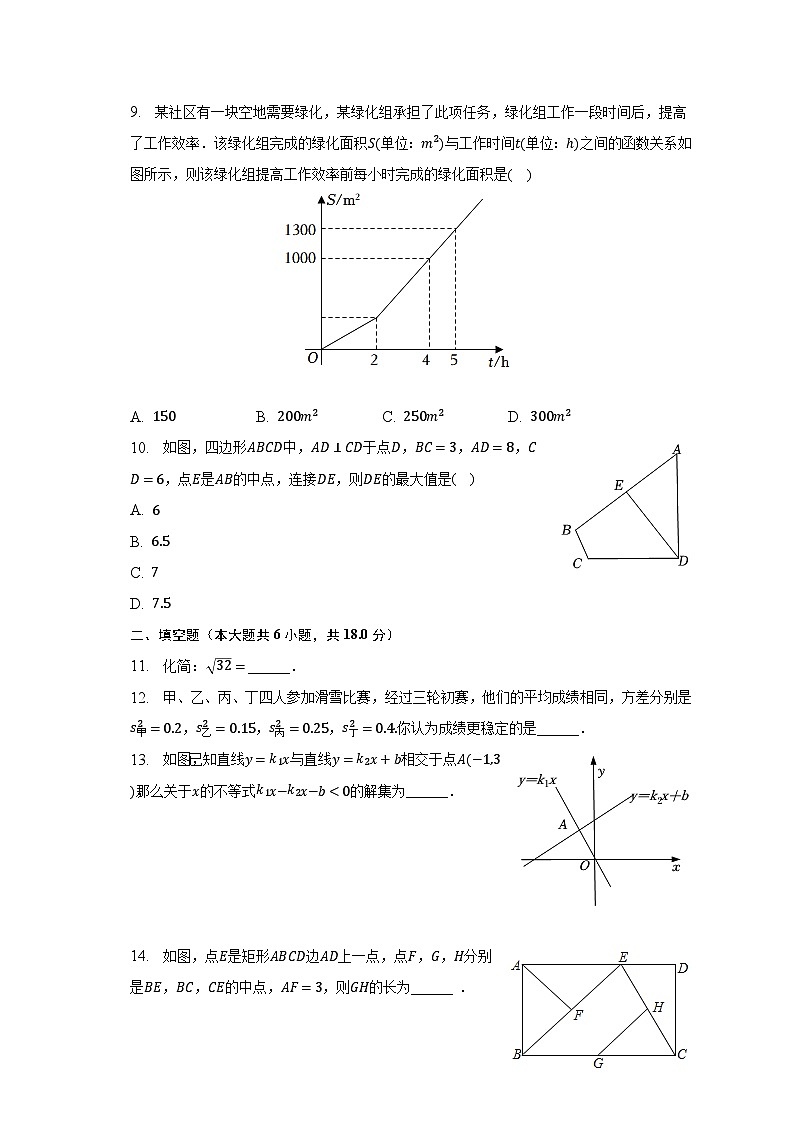
9. 某社区有一块空地需要绿化，某绿化组承担了此项任务，绿化组工作一段时间后，提高了工作效率．该绿化组完成的绿化面积S(单位：m2)与工作时间t(单位：h)之间的函数关系如图所示，则该绿化组提高工作效率前每小时完成的绿化面积是(    )

A. 150 B. 200m2 C. 250m2 D. 300m2
10. 如图，四边形ABCD中，AD⊥CD于点D，BC=3，AD=8，CD=6，点E是AB的中点，连接DE，则DE的最大值是(    )
A. 6
B. 6.5
C. 7
D. 7.5
二、填空题（本大题共6小题，共18.0分）
11. 化简： 32=______．
12. 甲、乙、丙、丁四人参加滑雪比赛，经过三轮初赛，他们的平均成绩相同，方差分别是s甲2=0.2，s乙2=0.15，s丙2=0.25，s丁2=0.4.你认为成绩更稳定的是______．
13. 如图，已知直线y=k1x与直线y=k2x+b相交于点A(−1,3)，那么关于x的不等式k1x−k2x−b0，b=−1−1 
【解析】解：∵直线y=k1x与直线y=k2x+b相交于点A(−1,3)，
根据图象可知，不等式k1x−k2x−b−1，
故答案为：x>−1．
根据一次函数的图象即可确定不等式的解集．
本题考查了一次函数与一元一次不等式的关系，熟练掌握一次函数的图象是解题的关键．

14.【答案】3 
【解析】解：在矩形ABCD中，∠BAD=90°，
∵F为BE的中点，AF=3，
∴BE=2AF=6．
∵G，H分别为BC，EC的中点，
∴GH=12BE=3，
故答案为3．
由矩形的性质及直角三角形斜边上的中线的性质可求解BE=2AF=6，再利用三角形中位线定理可求解．
本题主要考查矩形的性质，三角形的中位线定理，直角三角形斜边上的中线，求解BE的长是解题的关键．

15.【答案】258 
【解析】解：过点D作DE⊥BC交BC的延长线于点E，

由图象可知，点F由点A到点D用时为as，△FBC的面积为32acm2．
∴AD=a，
∴12BC⋅DE=12AD⋅DE=12a⋅DE=32a，
∴DE=3cm，
当点F从D到B时，用5s，
∴BD=5cm，
Rt△DBE中，BE= BD2−DE2=4(cm)，
∵四边形ABCD是菱形，
∴EC=4−a，DC=a，
在Rt△DEC中，a2=32+(4−a)2，
解得a=258(cm)．
故答案为：258．
通过分析图象，点F从点A到D用as，此时，△FBC的面积为32acm2，依此可求菱形的高DE，再由图象可知，BD=5，应用两次勾股定理分别求BE和a．
本题综合考查了菱形性质，勾股定理，一次函数图象性质，解答过程中要注意函数图象变化与动点位置之间的关系．

16.【答案】13 
【解析】解：如图：
∵高为12cm，底面周长为10cm，在容器内壁离容器底部3cm的点B处有一饭粒，
此时蚂蚁正好在容器外壁，离容器上沿3cm与饭粒相对的点A处，
∴A′D=5cm，BD=12−3+AE=12cm，
∴将容器侧面展开，作A关于EF的对称点A′，
连接A′B，则A′B即为最短距离，
A′B= A′D2+BD2= 52+122=13(Cm)．
故答案为：13
将容器侧面展开，建立A关于EF的对称点A′，根据两点之间线段最短可知A′B的长度即为所求．
本题考查了平面展开---最短路径问题，将图形展开，利用轴对称的性质和勾股定理进行计算是解题的关键．同时也考查了同学们的创造性思维能力．

17.【答案】解：(1) 32− 8+ 2
=4 2−2 2+ 2
=3 2；
(2)( 5+1)⋅ 5−12
=( 5)2−122
=5−12
=2． 
【解析】(1)先把每一个二次根式化成最简二次根式，然后再进行计算即可解答；
(2)利用平方差公式，进行计算即可解答．
本题考查了二次根式的混合运算，准确熟练地进行计算是解题的关键．

18.【答案】解：∵四边形ABCD是菱形，
∴BC=CD，∠ABC=∠ADC，
∵∠ABC+∠CBE=180°，
∠ADC+∠CDF=180°，
∴∠CBE=∠CDF，
在△CDF和△CBE中，
CD=CB∠CDF=∠CBEDF=BE，
∴△CDF≌△CBE(SAS)，
∴CE=CF． 
【解析】由四边形ABCD是菱形，得出BC=CD，∠ABC=∠ADC，根据等角的补角相等得出∠CBE=∠CDF，从而△CDF≌△CBE(SAS)即可．
本题主要考查了菱形的性质，以及全等三角形的判定与性质，证出∠CBE=∠CDF是解题的关键．

19.【答案】解：(1)根据题意得−4k+b=92k+b=3，
解得k=−1b=5，
所以一次函数解析式为y=−x+5；
(2)设点P(m,−m+5)，
∵点A(3,0)，
∴OA=3，
∵△OPA的面积为6，
∴△OPA的面积=12×AO×(−m+5)=6，
∴12×3×(−m+5)=6，
∴m=1，
∴点P(1,4)． 
【解析】(1)利用待定系数法求得即可；
(2)设点P(m,−m+5)，利用△OPA的面积=12×AO×(−m+5)=6，求出m即可求解．
本题考查了待定系数法求一次函数解析式，函数图象上点的坐标特征，三角形的面积．求出一次函数解析式是解题的关键．

20.【答案】解：(1)由条形图可知，喜爱B类节目的学生有60人，从扇形统计图中可得此部分占调查人数的20%，
本次抽样调查的样本容量是：60÷20%=300，
故答案为：300；
(2)喜爱C类电视节目的人数为：300−30−60−105−15=90(人)，
补全统计图如下：

(3)m%=105300×100%=35%，故m=35，
节目类型E对应的扇形圆心角的度数是：360°×15300=18°，
故答案为：35，18；
(4)该校1800名学生中喜欢新闻类节目的学生有：1800×30300=180(人)． 
【解析】(1)从条形统计图中可得到B人数为60人，从扇形统计图中可得此部分占调查人数的20%，可求出调查人数；
(2)总人数减去喜爱A、B、D、E类电视节目的人数，可得喜爱C类电视节目的人数，从而将条形图补全；
(3)根据百分比=所占人数÷总人数可得m的值；节目类型E对应的扇形圆心角的度数等于360°乘以节目类型E的百分比；
(4)利用样本估计总体的思想，用1800乘以样本中喜欢新闻类节目的学生百分比即可得出该校1800名学生中喜欢新闻类节目的学生人数．
本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．

21.【答案】(1)证明：∵四边形ABCD是平行四边形，
∴AB/​/CD，AB=CD，
∴∠BAE=∠CFE，∠ABE=∠FCE，
∵E为BC的中点，
∴EB=EC，
∴△ABE≌△FCE(AAS)，
∴AB=CF．

(2)解：当BC=AF时，四边形ABFC是矩形．
理由如下：∵AB/​/CF，AB=CF，
∴四边形ABFC是平行四边形，
∵BC=AF，
∴四边形ABFC是矩形． 
【解析】此题主要考查了全等三角形的判定，平行四边形的性质及矩形的判定等知识点的掌握情况．
(1)根据平行四边形的性质得到两角一边对应相等，利用AAS判定△ABE≌△FCE，从而得到AB=CF；
(2)由已知可得四边形ABFC是平行四边形，结合BC=AF，根据对角线相等的平行四边形是矩形，可得到四边形ABFC是矩形．

22.【答案】60  80 12 
【解析】解：(1)由图1可得，
甲的速度是120÷2=60(m/min)，
由图2可知，当x=67时，甲，乙两人相遇，
故乙的速度为：120÷67−60=80(m/min)，
故答案为：60，80；
(2)由图2可知：乙走完全程用了b min，甲走完全程用了a min，
则a=120÷60=2(min)，b=120÷80=32(min)，
∴2−32=12(min)．
故答案为：12；
(3)设甲出发xmin，甲、乙两人第二次相距60m．
 由题意得：60x+80x=120+60，
解得：x=97；
∴甲出发97min，甲、乙两人第二次相距60m．
(1)根据图1中的数据，可以计算出甲的速度，然后根据图2中的数据，可以计算出乙的速度，本题得以解决；
(2)根据题意，可知a是甲走完全程用的时间，b是乙走完全程用的时间，然后根据(1)中的结果和全程为120m，即可计算出a和b的值，本题得以解决；
(3)甲、乙两人第二次相距60m即相遇后相距60m，列方程即可求解．
本题考查了一次函数的应用，把一次函数和行程问题结合在一起，关键是明确三个量的关系：路程=时间×速度，利用数形结合的思想解答．

23.【答案】解：(1)由题意可知：
1200x=1500x+4，
解得：x=16；
经检验，x=16是原分式方程的解，且符合实际意义；
(2)设购进甲种水果m千克，则乙种水果(100−m)千克，利润为y，
由题意可知：
y=(20−16)m+(25−16−4)(100−m)=−m+500，
∵甲种水果的重量不低于乙种水果重量的3倍，
∴m≥3(100−m)，
解得：m≥75，即75≤m