备战2024年高考总复习一轮（数学）第3章 导数及其应用 第1节 导数的概念及运算课件PPT

这是一份备战2024年高考总复习一轮（数学）第3章 导数及其应用 第1节 导数的概念及运算课件PPT，共34页。PPT课件主要包含了内容索引，强基础固本增分，研考点精准突破，xx0，提示不一定，考向1求切线的方程，答案D等内容，欢迎下载使用。

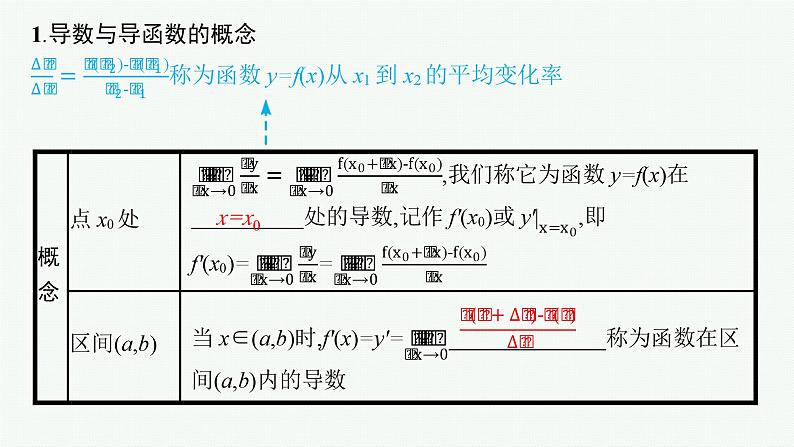
1.导数与导函数的概念
y-f(x0)=f'(x0)·(x-x0)
微点拨1.一般地,如果一个函数f(x)在区间(a,b)内的每一点x处都有导数,导数值记为f'(x),则f'(x)是关于x的函数,称f'(x)为f(x)的导函数,简称为导数.2.函数y=f(x)的导数f'(x)反映了函数f(x)的瞬时变化趋势,其正负号反映了变化的方向,其大小|f'(x)|反映了变化的快慢,|f'(x)|越大,曲线在这点处的切线越“陡峭”.
微思考1f'(x)与f'(x0)有什么不同?
微思考2直线与曲线相切,是不是直线与曲线只有一个公共点?
提示:f'(x)是一个函数,f'(x0)是函数f'(x)在x0处的函数值,是一个常数,[f'(x0)]'=0.
2.基本初等函数的导数公式
0　αxα-1　cs x　-sin x　ex　axln a
3.导数运算法则(1)[f(x)±g(x)]'=f'(x)±g'(x);(2)[f(x)g(x)]'=f'(x)g(x)+f(x)g'(x);
常用结论1.一般地,奇函数的导数是偶函数,偶函数的导数是奇函数,周期函数的导数还是周期函数.2.熟记以下结论:
答案:(1)D　(2)C　(3)D　
规律方法 常见形式及具体求导的方法
对点训练1求下列函数的导数.
解:(1)y'=(x2)'sin x+x2(sin x)'=2xsin x+x2cs x.
例2(1)(2021全国甲,理13)曲线 在点(-1,-3)处的切线方程为　　　　　. (2)(2022新高考Ⅱ,14)曲线y=ln|x|经过坐标原点的两条切线方程分别为　　　　　　　　,　　　　　　　　. 
规律方法 求曲线过点P的切线方程的方法(1)当点P(x0,y0)是切点时,切线方程为y-y0=f'(x0)(x-x0).(2)当点P(x0,y0)不是切点时,可分以下几步完成:第一步:设出切点坐标P'(x1,f(x1));第二步:写出过点P'(x1,f(x1))的切线方程y-f(x1)=f'(x1)(x-x1);第三步:将点P的坐标(x0,y0)代入切线方程求出x1;第四步:将x1的值代入方程y-f(x1)=f'(x1)(x-x1)可得过点P(x0,y0)的切线方程.
对点训练2(1) 曲线f(x)=2x+cs x在点 处的切线与两坐标轴围成的三角形面积是　　　　　. (2) 已知函数f(x)=ex+2x,过点(1,2)作曲线y=f(x)的切线,则函数的切线方程为　　　　　　　　　. 
考向2求曲线的切点坐标例3(1)设曲线y=ex+1上点P处的切线平行于直线x-y-1=0,则点P的坐标是　　　　. 
答案:(1)(0,2)　(2)ln 2　解析:(1)由题意,得y'=ex,且切线斜率为1,设切点为P(x,y),则ex=1,所以x=0,y=e0+1=2,故切点P的坐标为(0,2).
规律方法 已知切线方程(或斜率)求切点的一般思路是先求函数的导数,再让导数等于切线的斜率,从而求出切点的横坐标,将横坐标代入函数解析式求出切点的纵坐标.
对点训练3曲线y= 上一点P处的切线的斜率为-4,则点P的坐标为　 . 
考向3求参数的值(范围)例4(1)(2022四川成都二模)若曲线y=ln x+x2+1在点(1,2)处的切线与直线ax+y-1=0平行,则实数a的值为(　　)A.-4B.-3C.4D.3(2)(2022新高考Ⅰ,15)若曲线y=(x+a)ex有两条过坐标原点的切线,则a的取值范围是　　　　　. 
答案:(1)B　(2)(-∞,-4)∪(0,+∞)
规律方法 利用切点的坐标、切线的斜率、切线的方程等得到关于参数的方程(组)或者参数满足的不等式(组),进而求出参数的值或取值范围.
对点训练4若曲线f(x)=(ax-1)ex在x=0处的切线与直线x+y-6=0垂直,则a=(　　)A.0B.1C.2D.3
答案:C　解析:因为f(x)=(ax-1)ex,则f'(x)=(ax+a-1)ex,直线x+y-6=0的斜率为k=-1,由题意可得f'(0)=a-1=1,解得a=2.
考向4两曲线的公切线
规律方法 解两曲线公切线问题的两种方法
对点训练5已知函数f(x)=xln x,g(x)=x2+ax(a∈R),若经过点A(0,-1)存在一条直线l与f(x)图象和g(x)图象都相切,则a=(　　)A.0B.-1C.3D.-1或3
答案:D　解析:设直线l与f(x)=xln x相切的切点为(m,mln m),由f(x)=xln x的导数为f'(x)=1+ln x,可得切线的斜率为1+ln m,则切线的方程为y-mln m=(1+ln m)(x-m),将A(0,-1)代入切线的方程可得-1-mln m=(1+ln m)(0-m),解得m=1,则切线l的方程为y=x-1,联立 可得x2+(a-1)x+1=0,由Δ=(a-1)2-4=0,解得a=-1或3.