2023年广东省惠州市惠阳区中考数学模拟试卷(含答案)

2023年广东省惠州市 惠阳区 中考数学 模拟试卷

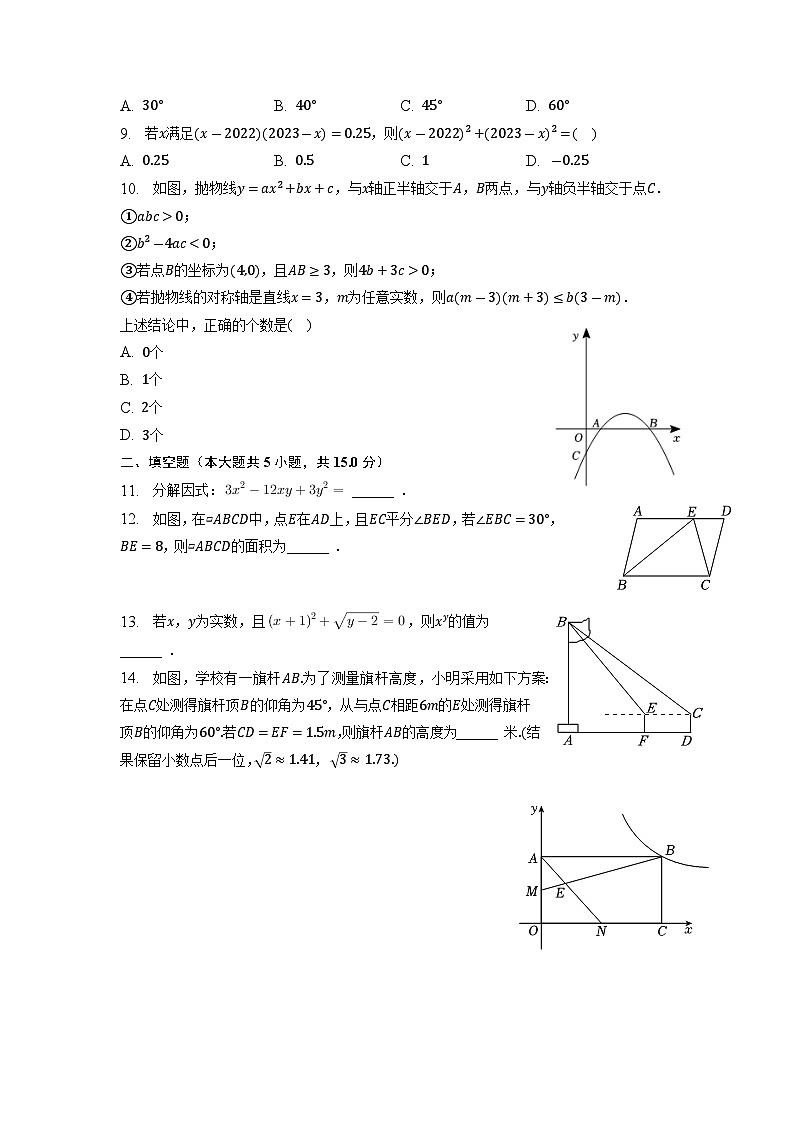
一、选择题（本大题共10小题，共30.0分）

1.  在实数，，，中，最小的数是(    )

A.  B.  C.  D.

2.  古语有云：“水滴石穿”，若水珠不断滴在一块石头上，经过年，石头上会形成一个深为的小洞数用科学记数法表示为(    )

A.  B.  C.  D.

3.  下列计算正确的是(    )

A.  B.
C.  D.

4.  在下面四个几何体中，俯视图是矩形的是(    )

A.  B.  C.  D.  

5.  如图，若，直线分别交，于点，，交于点，若，则(    )

A.
B.
C.
D.

6.  爱好运动的小颖同学利用“微信运动”这一公众号，连续记录了天每天的步数单位：万步分别为：，，，，，，，，则这组数据的中位数(    )

A.  B.  C.  D.

7.  等式有意义，则的取值范围为(    )

A.  B.  C.  D.

8.  如图，大建从点出发沿直线前进米到达点后向左旋转的角度为，再沿直线前进米，到达点后，又向左旋转角度，照这样走下去，第一次回到出发地点时，他共走了米，则每次旋转的角度为(    )

A.  B.  C.  D.

9.  若满足，则(    )

A.  B.  C.  D.

10.  如图，抛物线，与轴正半轴交于，两点，与轴负半轴交于点．
；
；
若点的坐标为，且，则；
若抛物线的对称轴是直线，为任意实数，则．
上述结论中，正确的个数是(    )

A. 个
B. 个
C. 个
D. 个

二、填空题（本大题共5小题，共15.0分）

11.  分解因式： ______ ．

12.  如图，在▱中，点在上，且平分，若，，则▱的面积为______ ．

13.  若，为实数，且，则的值为______ ．

14.  如图，学校有一旗杆为了测量旗杆高度，小明采用如下方案：在点处测得旗杆顶的仰角为，从与点相距的处测得旗杆顶的仰角为若，则旗杆的高度为______ 米结果保留小数点后一位，，

15.  如图，矩形的两边，在坐标轴上，且，，分别为，的中点，与交于点，且四边形的面积为，则经过点的反比例函数的解析式为______ ．

三、解答题（本大题共8小题，共75.0分）

16.  分已知关于的不等式组：只有个正整数解，求的取值范围．

17.  分先化简，再求值：，其中．

18.  分清明节，又称踏青节、行清节、三月节、祭祖节等，节期在仲春与暮春之交，是中华民族最隆重盛大的祭祖大节清明节兼具自然与人文两大内涵，既是自然节气点，也是传统节日，扫墓祭祖与踏青郊游是清明节的两大礼俗主题，这两大传统礼俗主题在中国自古传承，至今不辍某学校数学兴趣小组为了了解该校学生对清明节的了解情况，在全校范围内随机抽取一部分学生进行问卷调查，并将调查结果适当整理后绘制成如下两幅不完整的统计图．

本次调查抽查了______ 人，请补全条形统计图；
本次调查的中位数落在______ 填了解程度，扇形图中“了解一点”对应的扇形的圆心角为______ 度；
已知该学校共有人，请你估计该校学生对清明节“不了解”的人数．

19.  分世界杯火热进行期间，其相关的周边产品大多为中国制造为了抓住这一商机，两工厂决定生产球衣据统计，甲厂每小时生产件，乙厂每小时生产件甲、乙两厂共生产小时，且每天生产的球衣总数量为件．
求甲、乙两厂每天分别生产多少小时？
由于球衣在国外热销，客户纷纷追加订单，两工厂每天均增加生产时间，其中甲厂比乙厂多增加小时，在整个生产过程中，甲厂每小时产量不变，而乙厂由于机器损耗及人员不足，每增加一个小时，每小时产量将减少件，这样两工厂一天生产的球衣总量将比原来多件求甲厂增加的生产时间为多少小时？

20.  分如图，一次函数与反比例函数的图象交于点和，与轴交于点．
求一次函数和反比例函数的解析式；
若点关于原点的对称点为，求的面积．

21.  分如图，半径是的中，与相切于点，与交于点，点是延长线上一点，且，是半圆上的一点，．
求的度数；
求证：是的切线；
求图中阴影部分的面积．

22.  分已知，在四边形中，，，连、，如图．

求的度数；
以为对角线，为边作平行四边形，如图，试判断直线与的位置关系，并说明理由．
在的条件下，若，，直接写出的长．

23.  分如图，在平面直角坐标系中，抛物线与轴分别交于，两点，点的坐标是，点的坐标是，与轴交于点，是抛物线上一动点，且位于第二象限，过点作轴，垂足为，线段与直线相交于点．

求该抛物线的解析式；
如图，若线段将分成面积比为：两部分，求点的坐标；
如图，连接，是否存在点，使得，若存在，求出点的横坐标；若不存在，请说明理由．

1.     2.    3.    4.    5. 

6.     7.    8.    9.    10. 

11.     12.     13.      14.      15. 

16.解：由，得，
由，得，
当时，，
关于的不等式组：只有个正整数解，
不符合题意；
当，即时，，
不等式组的解集为，
不等式组：只有个正整数解，
，
解得，
的取值范围． 

17.解：


，
．
原式． 

18.解：由题意得，样本容量为：35÷35%=100，
非常了解的人数为：100×40%=40（人），
补全条形统计图如下：

（2）由统计图可知，本次调查的中位数落在比较了解，
扇形图中“了解一点”对应的扇形的圆心角为：360°×=54°；
故答案为：比较了解；54；
（3）600×=60（人），
答：该校学生对清明节“不了解”的人数约为60人．

19.解：设甲厂每天生产小时，乙厂每天生产小时，
根据题意得：，
解得：．
答：甲厂每天生产小时，乙厂每天生产小时；
设甲厂增加的生产时间为小时，则乙厂增加的生产时间为小时，乙厂每小时生产件，
根据题意得：，
整理得：，
解得：，，
当时，，不符合题意，舍去，
．
答：甲厂增加的生产时间为小时． 

20.解：把代入得：
，
反比例函数的解析为：．
点在反比例函数的图象上，
，
，
把，代入得
，
解得．
一次函数的解析式为：．
关于原点的对称点为，
．
和到轴的距离是．
在直线上，且在轴上，
，
．
，
． 

21.解：如图所示，连接，，

与相切于点，
，
，

，
是等边三角形，
，

；
证明：如图所示，连接，

，，
在中，，
，
，
，
，
，
，
，
，
在，中，
，
≌，
，
即，
是的切线；
解：，
，
，，



． 

22.解：如图，延长至，使，连接，

，，
，
，
，
，
在和中，
，
≌
，，
，
，
是等腰直角三角形，
，
．
，
理由：延长至，使，连接，连接交于，

平行四边形，
，，
，
，
，
由知，
，
，
，
，
在与中，
，
≌，
，，
，
，即，
，
，，，
，
，
，
，
．
延长至，使，连接，延长交于，

由知：，是等腰直角三角形，
由：，，

，
由知：是等腰直角三角形，
，，
，
在中，设，则，
由勾股定理，得，
解得：，
，
在中，由勾股定理，得． 

23.解：把，代入得：
，
解得，
抛物线的解析式为；
设，则，
在中，令得，
，
，
由，得直线的解析式为，
，
，，
，
由线段将分成面积比为：两部分，分两种情况：
当时，
，
解得或此时在第三象限，舍去，
；
当时，
，
解得或此时在第三象限，舍去，
；
综上所述，的坐标为或；
存在点，使得，理由如下：
延长到，设，连接，如图：

，
，
，
，
，
，
，
，
设，则，，
，
，
，
，
，
整理化简得，
，
解得舍去或大于，舍去或，
点的横坐标为．