2023届山西省太原市清徐县数学六年级第二学期期末学业水平测试试题含解析

2023届山西省太原市清徐县数学六年级第二学期期末学业水平测试试题

一、认真填一填。

1．松树有8棵，杨树有11棵，松树的棵数是杨树的___，杨树的棵数是松树的_____．

2．6085dm3＝（______）m3；785ｍl＝（______）cm3＝（______）dm3。

3．一共有140人参加庆“六一”文艺演出活动，其中女生的人数比男生多，男生的人数是女生的 ，男生的人数是总人数的 ．

4．一块体积为32m3的长方体大理石,底面积是8m2,高是（____）米．

5．一个数的最大因数是72，这个数的最小倍数是________，把这个数分解质因数________。

6．的分数单位是（______），再添上（______）个这样的分数单位是；将减少（______）个这样的分数单位是。

7．写出下面每个分数中分子和分母的最大公因数或最小公倍数．

最大公因数：（________）               最小公倍数：________

8．在括号里填上合适的体积单位或容积单位。 

一台冰箱的容积约是150______；一个热水杯的容积约是200______。

一个苹果的体积约是130_____；一个讲台的体积约是0.6_____。

9．（      ）÷（       ）＝＝0.375＝

10．爸爸将100元的给姐姐，妈妈将100个元给弟弟，姐姐又将爸爸给自己的钱的给弟弟.那么，妈妈和姐姐一共给了弟弟（_______）元钱.

二、是非辨一辨。

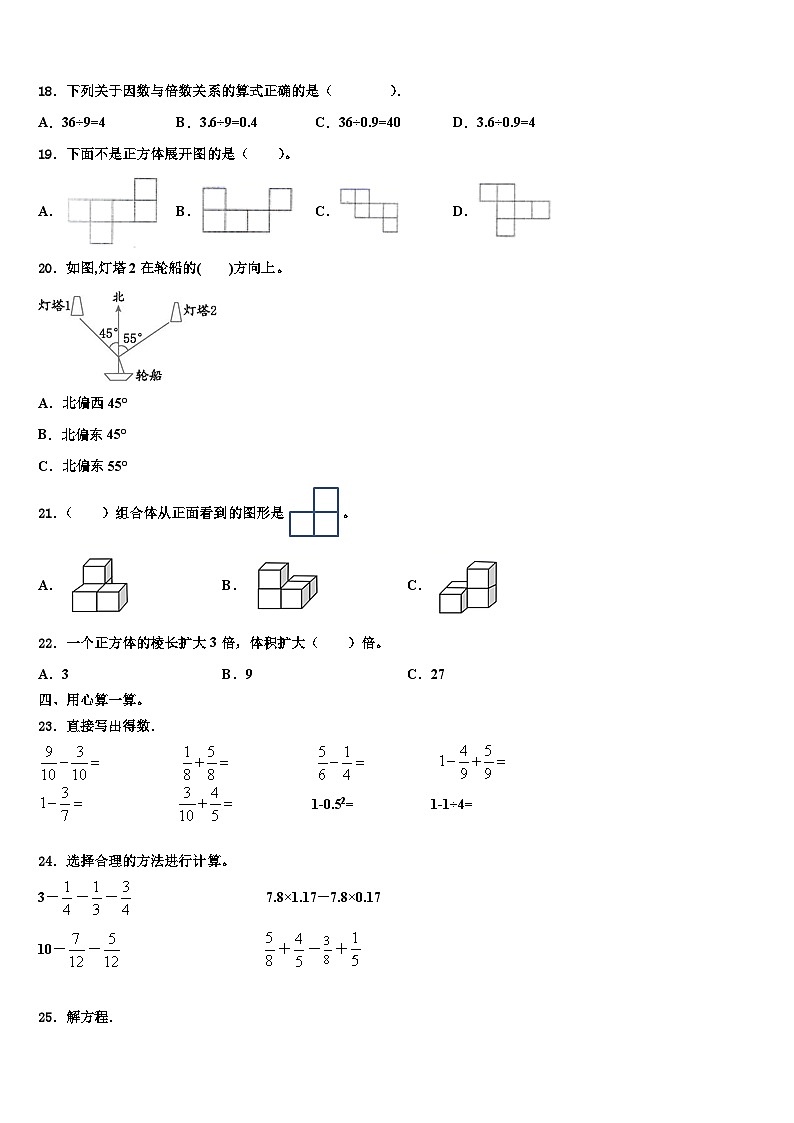
11．一个数既是2的倍数，又是3的倍数，它一定是6的倍数．   （_______）

12．1千克的5/6与5千克的1/6一样重。（____）

13．＝＝6÷(  )＝(  )(填小数)。

14．一个数的倍数一定比它的因数大。（________）

15．运用分数的基本性质可以写出“＝”这样的等式。 （____）

16．大于而小于的真分数有无数个．           （_______）

三、细心选一选。请把正确答案的序号填在括号里。

17．一个圆的半径扩大2倍，周长也扩大2倍。（______）

18．下列关于因数与倍数关系的算式正确的是（        ）．

A．36÷9=4 B．3.6÷9=0.4 C．36÷0.9=40 D．3.6÷0.9=4

19．下面不是正方体展开图的是（    ）。

A． B． C． D．

20．如图,灯塔2在轮船的(　　)方向上。

A．北偏西45°

B．北偏东45°

C．北偏东55°

21．（    ）组合体从正面看到的图形是。

A． B． C．

22．一个正方体的棱长扩大3倍，体积扩大（　　）倍。

A．3 B．9 C．27

四、用心算一算。

23．直接写出得数．

                        1-0.52=           1-1÷4=

24．选择合理的方法进行计算。

3－－－                   7.8×1.17－7.8×0.17

10－－                    ＋－＋

25．解方程．

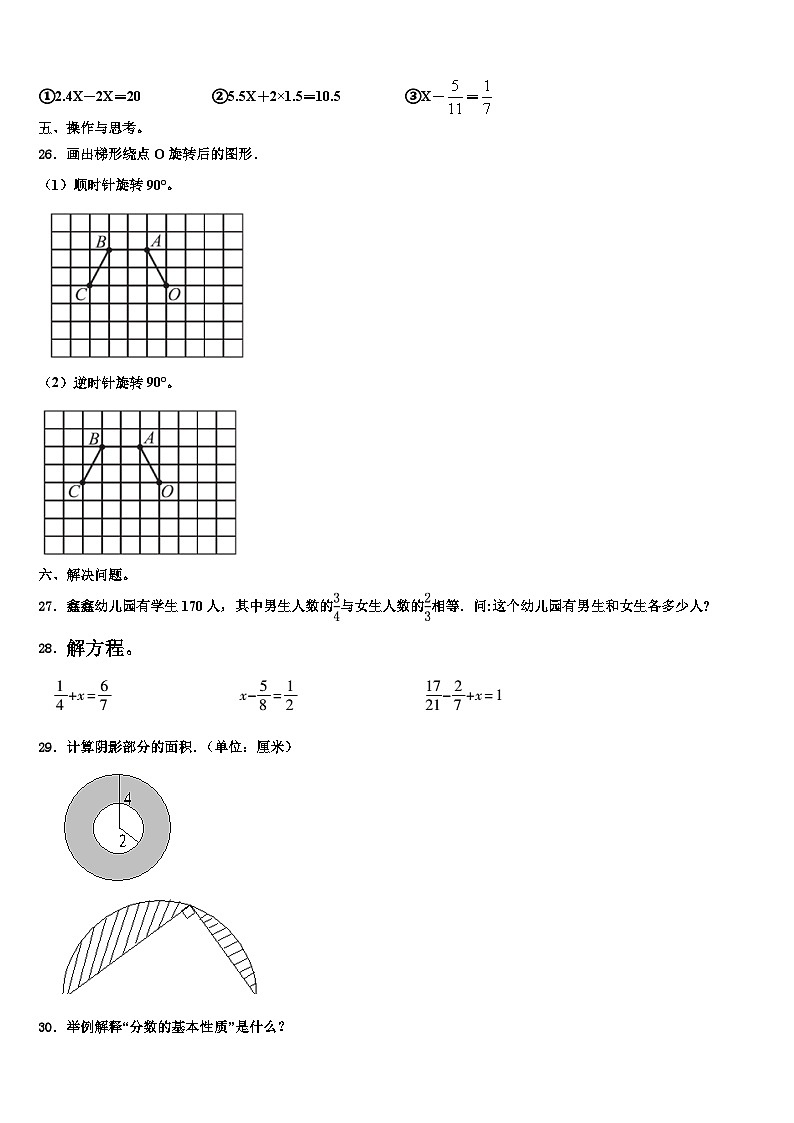
①2.4X－2X＝20          ②5.5X＋2×1.5＝10.5         ③X－＝

五、操作与思考。

26．画出梯形绕点O旋转后的图形．

（1）顺时针旋转90°。

（2）逆时针旋转90°。

六、解决问题。

27．鑫鑫幼儿园有学生170人，其中男生人数的与女生人数的相等．问:这个幼儿园有男生和女生各多少人?

28．解方程。

29．计算阴影部分的面积．（单位：厘米）

30．举例解释“分数的基本性质”是什么？

31．服装厂要做500套校服，计划20天完成。平均每天做多少套？平均每天完成这批校服的几分之几？

32．只列式不计算

一个长方体粮仓从里面量长6m，宽4m，高2m，如果每立方米稻谷重550kg，这个粮仓能装稻谷多少千克？

33．王阿姨买了3千克橘子和4千克苹果，共用去32.4元。橘子每千克3.6元，苹果每千克多少元？

参考答案

一、认真填一填。

1、       

【解析】用松树的棵数除以杨树的棵数，即为松树是杨树的几分之几；用杨树的棵数除以松树的棵数，即为杨树是松树的几分之几．

【详解】8÷11＝

11÷8＝

答：松树的棵数是杨树的，杨树的棵数是松树的．

故答案为；．

2、6.085    785    0.785   

【分析】（1）立方分米和立方米之间的进率是1000，把6085立方分米换算成立方米，用6085除以进率1000，即小数点向左移动三位即可；

（2）1毫升＝1立方厘米，立方厘米和立方分米之间的进率是1000，把785立方厘米换算成立方分米，用785除以进率1000，即小数点向左移动三位，数位不够，整数部分要补0；

【详解】6085dm3＝6.085

785mL＝785＝0.785 dm3

主要考查体积单位的换算，把低级单位换算成高级单位，要除以单位间的进率；要注意位数不够时，要在整数部分和小数部分补0。

3、 ；

【详解】略

4、4

【详解】本题要求这块大理石的高是多少米,要根据“长方体的体积=底面积×高”变形为“长方体的高=体积÷底面积”来列式计算．

5、72    72＝2×2×2×3×3   

【分析】根据因数和倍数的知识，一个数的最大因数和最小倍数都是它自己；分解质因数就是把一个合数写成几个质数的连乘的形式，一般先从简单的质数试着分解，然后把所有的质数相乘。

【详解】一个数的最大因数是72，这个数的最小倍数是72，72＝2×2×2×3×3。

故答案为：72；72＝2×2×2×3×3。

此题主要考查了因数和倍数的知识以及分解质因数的方法。找一个数的因数时一定要一对一对的找，不要漏掉。

6、    1    1   

【分析】根据分数单位的意义，把单位“1”平均分成若干份，表示其中1份的数叫分数单位，也就是分母分之一。

【详解】根据分数单位的意义可知的分数单位是，＝，－＝所以再添上1个这样的分数单位是，＝，－＝，所以减少1个这样的分数单位是。

本题考查分数的意义，明确分数单位的意义是解决本题的关键。

7、15    18   

【解析】略

8、L    mL    c       

【解析】根据实际情况选择合适的体积单位或容积单位。

【详解】一台冰箱的容积约是150L；

一个热水杯的容积约是200mL；

一个苹果的体积约是130cm3；

一个讲台的体积约是0.6m3。

故答案为：L；mL；cm3；m3。

9、3  8  3  64

【详解】略

10、24

【解析】略

二、是非辨一辨。

11、√

【详解】同时是2和3的倍数的数一定是1的倍数，因为同时是2和3的倍数的数最小的数是1．

12、√

【解析】略

13、30 10 0.6

【解析】略

14、×

【分析】一个数的倍数的个数是无限的，最小的是它本身，没有最大的倍数；一个数的因数的个数是有限的，最小的因数是1，最大的因数是它本身，据此判断即可。

【详解】由分析可知：一个数最大的因数＝最小的倍数＝这个数本身，并不是这个数所有的因数都比它的倍数小，所以本题说法错误。

故答案为：×。

本题主要考查对因数倍数的认识，解答本题的关键是掌握一个数最大的因数＝最小的倍数＝这个数本身。

15、×

【解析】略

16、√

【解析】略

三、细心选一选。请把正确答案的序号填在括号里。

17、√

【解析】略

18、A

【详解】略

19、B

【分析】正方体展开图有：“1－4－1”型；“2－3－1”型；“2－2－2”型；“3－3”型，共计11种；据此解答。

【详解】A，符合“1－4－1”型，是正方体展开图；

B，只有5个面，不是正方体的展开图；

C，符合“2－3－1”型，是正方体展开图；

D，符合“2－3－1”型，是正方体展开图；

故答案为：B。

本题主要考查正方体的展开图，牢记11种正方体展开图是解题的关键。

20、C

【解析】本题中灯塔2在轮船的右上方与正北方向成55°角的位置,即北偏东55°方向上。

21、C

【分析】根据观察者观察位置的变化，我们可以发现观察者所看到的被观察的对象的范围也随着发生相应的变化。

【详解】从正面看，A.，B.，C.。

故答案为：C

本题考查了观察物体，从不同角度方向观察物体，常常得到不同的结果。

22、C

【分析】正方体的体积等于棱长的立方，它的棱长扩大几倍，则它的体积扩大棱长扩大倍数的立方倍。

【详解】正方体的棱长扩大3倍，它的体积则扩大3³=27倍；

故选：C

四、用心算一算。

23、；；；

；；0.75；

【详解】略

24、；7.8

9；

【分析】（1）由减法的性质：连续减去两个数等于减去这两个数的和可得：原式＝3－（＋）－；由此进行简算；（2）可运用乘法分配律进行简算；（3）可运用减法的性质进行简算；（4）可运用加法交换律与结合律进行简算；据此解答

【详解】3－－－

＝3－（＋）－

＝3－1－

＝2－

＝

7.8×1.17－7.8×0.17

＝7.8×（1.17－0.17）

＝7.8×1

＝7.8

10－－

＝10－（＋）

＝10－1

＝9

＋－＋

＝（－）＋（＋）

＝＋1

＝

故答案为：；7.8；9；

本题考查了分数的加减混合运算以及小数的混合运算，关键是要仔细观察式中的数据，运用合适的方法进行简算。

25、①X＝50    ②X＝     ③X＝

【详解】略

五、操作与思考。

26、（1）如图

（2）如图

【分析】在平面内，讲一个图形绕一个图形按某一方向转动一个角度，这样的运动叫做图形的旋转。这个定点叫做旋转中心，转动的角度叫做旋转角。

【详解】（1）如图

（2）如图

本题考查旋转的相关知识，需要明白旋转前后图形的大小和形状没有发生改变。

六、解决问题。

27、解：设男生有x人。

x＝(170－x)×

x＝80

170－80＝90(人)

答：这个幼儿园有男生80人，女生90人。

【解析】略

28、

【解析】略

29、15.25平方厘米  12π平方厘米；

【解析】略

30、分数的分子和分母同时乘或除以相同的数（除外），分数的大小不变这叫做分数的基本性质。

比如：，表示单位“1”的一半，表示单位“1”的一半。

【分析】分数的分子和分母同时乘或除以相同的数（除外），分数的大小不变这叫做分数的基本性质；再举几个例子即可。

【详解】分数的分子和分母同时乘或除以相同的数（除外），分数的大小不变这叫做分数的基本性质。

比如：，表示单位“1”的一半，表示单位“1”的一半。

本题主要考查对分数的基本性质的理解。

31、500÷20＝25(套) 1÷20＝

答：平均每天做25套，平均每天完成这批校服的。

【解析】略

32、6×4×2×550

【解析】略

33、5.4元

【分析】根据题意可知，橘子的重量×单价＋苹果的重量×单价＝总价格，可以设苹果每千克x元，根据等量关系式列出方程：3×3.6＋4x＝32.4，再根据等式的性质解方程，求出的方程的解就是苹果的单价。

【详解】解：设苹果每千克x元

3×3.6＋4x＝32.4

10.8＋4x＝32.4

4x＝32.4－10.8

4x＝21.6

x＝21.6÷4

x＝5.4

答：苹果每千克5.4元。

此题主要考查了学生利用方程解决解答实际问题的能力，列方程解决问题的大致步骤是：（1）根据题意找准等量关系式；（2）设未知数x，根据等量关系列方程；（3）解方程；（4）检验并写答。