2023届歙县数学六下期末教学质量检测模拟试题含解析

2023届歙县数学六下期末教学质量检测模拟试题

一、仔细推敲，细心判断。（对的打“√ ”，错的打“×”）

1．把2个同样大小的蛋糕平均分给4个小朋友，每人分得个蛋糕． （______）

2．棱长之和相等的两个正方体，它们的体积相等．（_______）

3．三角形是轴对称图形。（______）

4．把一根钢管锯成一样长的小段，锯了6次，每段占全长的。（______）

5．一个正方体的棱长之和是12cm，它的体积就是8cm³。（______）

二、反复思考，慎重选择。（将正确答案的序号填在括号里）

6．两个相邻自然数的最小公倍数是42，这两个自然数的和是（    ）。

A．12 B．13

C．14 D．15

7．如果甲数的等于乙数的（甲数、乙数都不为0），那么甲数（     ）乙数。

A．小于 B．等于 C．大于

8．如果 是偶数， 是奇数，那么下面计算结果是偶数的式子是（  ）

A．2a+b B．a+2b C．a+b

9．以下说法正确的有（    ）个

①把一根绳子剪成两段，第一段长m，第二段占全长的，则第二段更长

②把一根绳子剪成两段，第一段占全长的，第二段占全长的，则第二段更长

③有两根长3米的绳子，第一根剪去，第二根剪去米，剪去的部分比较，第一根更长．

A．0 B．1 C．2 D．3

10．有三个分数，分子都是1，分母分别是最小的质数、最小的合数、奇数中最小的质数。三个分数之和是（      )

A．1    B．1    C．1    D．1

三、用心思考，认真填空。

11．小敏家电子钟的分针从“3”走到“5”，按（_____）时针方向旋转了（_____）。

12．将一条长度为 9 米的皮绳反复对折 3 次后，长为（___）米。

13．60与15的最大公因数是（________），最小公倍数是（________）。

14．里面有（______）个；8个是（______）；里面有（______）个。

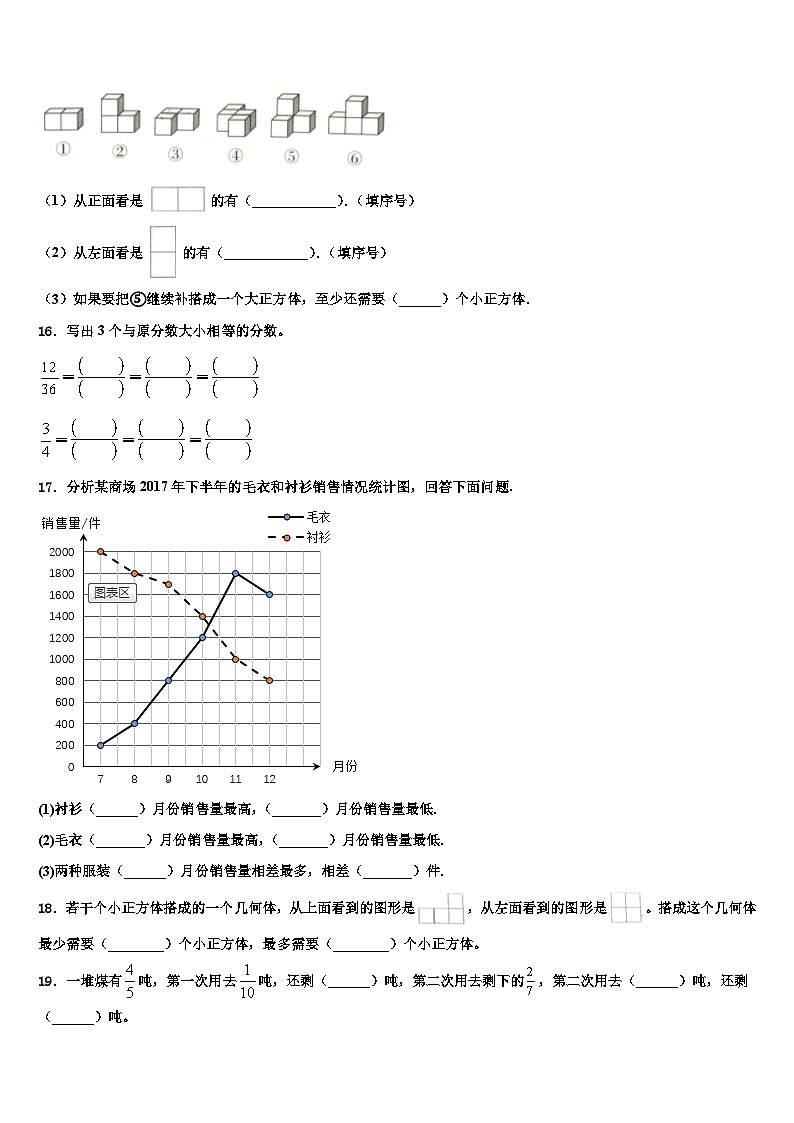
15．下面是用小正方体搭建的一些几何体．

（1）从正面看是的有（____________）．（填序号）

（2）从左面看是的有（____________）．（填序号）

（3）如果要把⑤继续补搭成一个大正方体，至少还需要（______）个小正方体．

16．写出3个与原分数大小相等的分数。

＝＝＝

＝＝＝

17．分析某商场2017年下半年的毛衣和衬衫销售情况统计图，回答下面问题.

(1)衬衫（______）月份销售量最高，（_______）月份销售量最低.

(2)毛衣（_______）月份销售量最高，（_______）月份销售量最低.

(3)两种服装（______）月份销售量相差最多，相差（_______）件.

18．若干个小正方体搭成的一个几何体，从上面看到的图形是，从左面看到的图形是。搭成这个几何体最少需要（________）个小正方体，最多需要（________）个小正方体。

19．一堆煤有吨，第一次用去吨，还剩（______）吨，第二次用去剩下的，第二次用去（______）吨，还剩（______）吨。

20．在3、4、12、15、17、53、320中，奇数有____________，偶数有__________；质数有____________，合数有_____________。

四、注意审题，用心计算。

21．直接写出得数．

22．计算下面各题。（能简算的要简算）

23．解方程。

＋x＝     x－＝

五、看清要求，动手操作。（7分）

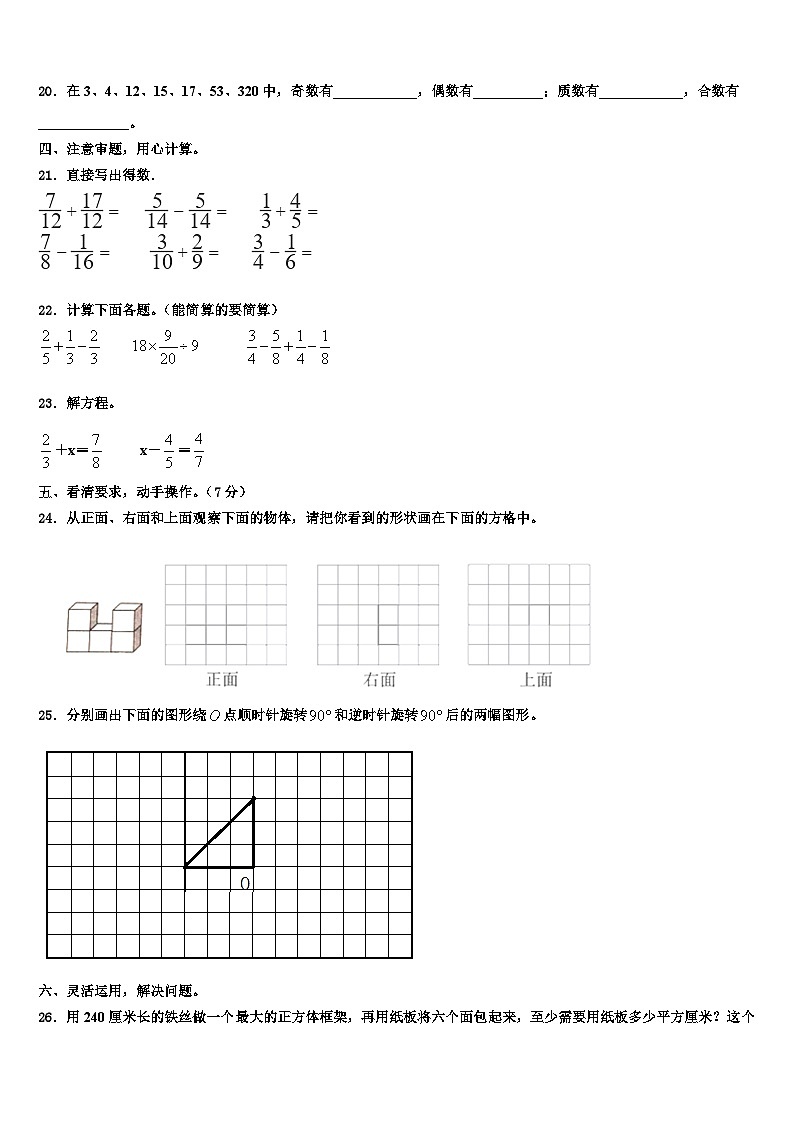
24．从正面、右面和上面观察下面的物体，请把你看到的形状画在下面的方格中。

25．分别画出下面的图形绕点顺时针旋转和逆时针旋转后的两幅图形。

六、灵活运用，解决问题。

26．用240厘米长的铁丝做一个最大的正方体框架，再用纸板将六个面包起来，至少需要用纸板多少平方厘米？这个纸盒的体积是多少立方厘米？

27．如图，把一根长2米的长方体钢材截成三段，表面积比原来增加2.4平方分米，这根钢材原来的体积是多少立方分米？

28．五（一）班同学做游戏，每8人一组，每12人一组都刚好分完。这个班同学在40人50人之间，这个班有多少人？

29．先完成统计图，然后根据折线统计图回答问题。

某电脑公司2013年每月收入支出情况统计

（1）几月收入和支出相差最小？

（2）9月收入和支出相差多少万元？ 

（3）全年共计收入多少万元？  

（4）平均每月支出多少万元？

30．亮亮家要给一个长0.75m，宽0.5m，高1.6m的简易衣柜换布罩，（如下图，没有底面）。至少需要用布多少平方米？

参考答案

一、仔细推敲，细心判断。（对的打“√ ”，错的打“×”）

1、×

【分析】求每人分得几分之几个蛋糕，平均分的是具体的数量两个同样大小的蛋糕，表示把2个蛋糕平均分成4份，求的是具体的数量，用2÷4计算得解．

【详解】2÷4=（个）；

答：每人分得个蛋糕．

故判断为：错误．

2、√

【详解】因为正方体的棱长是固定的一个数，两个正方体的棱长之和相等，那么这两个正方体的棱长相等，正方体的体积是棱长×棱长×棱长，所以这两个正方体的体积相等，所以该说法恶化那个却．故答案为√．

3、×

【分析】如果一个图形沿着一条直线对折，直线两边的图形能够完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴；据此判断即可解答。

【详解】根据轴对称图形的意义可知，所有的三角形中等腰三角形和等边三角形是轴对称图形，其它的一般三角形不是轴对称图形；所以，三角形不一定都是轴对称图形。

故答案为：×。

本题主要考查学生对轴对称图形定义的理解和掌握，以及灵活运用定义来判断轴对称图形。

4、×

【分析】锯了6次，实际上是锯成了7段，求每段长占全长的几分之几，表示把这根钢管看作单位“1”，把单位“1”平均分成7份，求的是每一份占的分率，平均分的是单位“1”；用除法计算得解。

【详解】1÷（6＋1）

＝1÷7

＝

故答案为：×。

解决此题关键是明确：锯的段数比次数多一；进而根据分数的意义得解。

5、×

【分析】用棱长总和÷12，先求出棱长，再根据正方体体积＝棱长×棱长×棱长，求出体积即可。

【详解】12÷12＝1（厘米）

1×1×1＝1（立方厘米）

一个正方体的棱长之和是12cm，它的体积就是1cm³，所以原题说法错误。

本题考查了正方体棱长总和及体积，正方体有12条棱，每条棱的长度相等。

二、反复思考，慎重选择。（将正确答案的序号填在括号里）

6、B

【分析】因为两个相邻自然数的最小公倍数是42，那么这两个相邻自然数一定互质，互质的两个自然数的最小公倍数就是这两个数的乘积，先想乘法，确定这两个数，再求出两个自然数的和即可。

【详解】6×7＝42，所以这两个自然数分别是6和7。

6＋7＝13，它们的和是13，故选择B。

如果相邻两个自然数不是0和1，不是1和2时，这两个自然数就互质。同时理解并灵活运用“互的两个自然数的最小公倍数就是这两个数的乘积”是解决本题的关键。

7、C

【解析】略

8、B

【详解】奇数+奇数=偶数，偶数+偶数=偶数，偶数+奇数=奇数．整数中，能被2整除的数叫做偶数，不能被2整除的数叫做奇数．

9、C

【详解】把一根绳子剪成两段，第二段占全长的，则第一段占1-=，>，第二段更长，所以①正确；

把这根绳子看做单位“1”，而把一根绳子剪成两段，第一段占全长的，第二段占全长的，+=>1，这样是不可能的，所以②错误；

有两根长3米的绳子，第一根剪去，减去了1.5米，第二根减去米，1.5米>米，剪去的部分比较，第一根更长，所以③正确．

故答案为C．

10、C

【解析】略

三、用心思考，认真填空。

11、顺    60°   

【解析】略

12、

【解析】略

13、15    60   

【分析】两数成倍数关系，最大公因数是较小的数，最小公倍数较大的数。

【详解】60＝15×4，60与15的最大公因数是15，最小公倍数是60。

如果一个整数同时是几个整数的因数，称这个整数为它们的“公因数”；公因数中最大的称为最大公因数（最大公约数）。两个或多个整数公有的倍数叫做它们的公倍数，其中除0以外最小的一个公倍数就叫做这几个整数的最小公倍数。

14、3        3   

【分析】表示把单位“1”平均分成5份，取其中的3份，即里面有3个；是把单位“1”平均分成7份，取其中的8份是；＝，所以里面有3个。

【详解】由分析可得：

里面有3个；8个是；里面有3个。

故答案为：3；；3

考查了分数的意义，把单位“1”平均分成若干份，表示其中一份的叫分数单位。

15、①③④    ②⑥    4   

【解析】略

16、；；

；；

【分析】本题是根据分数的基本性质来解答的，对于，可以把分子、分母同时缩小、、，就可得到与原分数大小相等但分子、分母都较小的分数；对于，可以把分子分母同时扩大2倍、3倍、4倍，就可得到与原分数大小相等但分子分母都较大的分数。

【详解】

应用分数的基本性质时，①要注意分子分母必须同时变化，②要注意同时乘或除以的数不为0。

17、7    12    11    7    7    1800   

【解析】略

18、6    8   

【分析】最少如图（情况不唯一），最多如图，数出个数即可。

【详解】搭成这个几何体最少需要6个小正方体，最多需要8个小正方体。

本题考查了观察物体，可以画一画示意图，或有较强的空间想象能力。

19、           

【解析】略

20、3、15、17、53    4、12、320    3、17、53    4、12、15、320   

【分析】奇数：末尾是1、3、5、7、9的数；

偶数：末尾是0、2、4、6、8的数；

质数：只有1和它本身两个因数；

合数：除了1和它本身外还有其他因数；

据此选择合适的数填写即可。

【详解】奇数有：3、15、17、53；

偶数有：4、12、320；

质数有：3、17、53；

合数有：4、12、15、320

掌握奇数、偶数、质数和合数的特征是解决此题的关键。

四、注意审题，用心计算。

21、2；0； ；

 ； ；

【详解】同分母分数相加或相减，分母不变，只把分子相加或相减即可；异分子分母分数相加或相减，先通分把他们化成分母相同的分数，然后按照同分母分数相加或相减的方法来计算，能约分的要约分．

22、；；

【分析】（1）根据题意，可先计算减法，再计算加法；

（2）根据除以一个数相当于乘以它的倒数，将原式变为，交叉约分即可；

（3）根据加法交换律和结合律，将原式变为，然后先算加法再算减法即可解答。

【详解】

＝

＝

＝

＝

＝

＝

＝1－

＝

此题主要考查学生对分数混合运算的简算方法的掌握与应用，其中需要掌握加法交换律：a＋b＝b＋a，加法结合律：（a＋b）＋c＝a＋（b＋c）。

23、x＝；x＝

【分析】（1）根据等式的性质方程的两边同时－求解。

（2）根据等式的性质方程的两边同时＋求解。

【详解】（1）＋x＝    

解：x＝－

x＝－

x＝

（2）x－＝

解：x＝＋

x＝＋

x＝

异分母分数相加减，先化为同分母分数再计算。

五、看清要求，动手操作。（7分）

24、

【分析】从正面看，有两层，下层有3个小正方形，上层有2个小正方形，中间空一格；从右面看有两层，上下各1个小正方形；从上面看有一排，并排3个，据此画图即可。

【详解】由分析可知，从正面、右面、上面看到的图形如下：

此题考查立体图形的三视图画法，认真观察，分析各个面上小正方形的相对位置再画图。

25、

【分析】根据旋转的特征，图形绕点顺（逆）时针旋转90°，点的位置不动，其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。

【详解】根据分析，分别画出图形绕点顺时针旋转 90°（图中红色部分）和逆时针旋转 90°（图中蓝色部分）后的图形如下：

旋转作图要注意：①旋转中心；②旋转方向；③旋转角度。整个旋转作图，就是把整个图案的每一个特征点绕旋转中心按一定的旋转方向和一定的旋转角度旋转移动。

六、灵活运用，解决问题。

26、2400平方厘米   8000立方厘米

【解析】铁丝的长度是框架的棱长和，除以12即可求出正方体的棱长，然后根据公式分别计算需要纸的面积和纸盒的体积．正方体表面积=棱长×棱长×6，正方体体积=棱长×棱长×棱长．

【详解】240÷12=20（厘米）；20×20×6=2400（平方厘米）；20×20×20=8000（立方厘米）．

答：至少需要2400平方厘米纸板，这个纸盒的体积是8000立方厘米．

27、12立方分米

【分析】增加的表面积是增加的4个截面的面积．2.4除以4得到每个截面的面积，再乘长就得到钢材原来的体积．

【详解】2米＝20分米

2.4÷4×20＝12(立方分米)

答：这根钢材原来的体积是12立方分米．

28、48人

【分析】五（一）班同学做游戏，每8人一组，每12人一组都刚好分完，说明这个班同学的人数是8和12的公倍数，而且在40人50人之间，据此解答即可。

【详解】在50以内8和12的倍数：

8的倍数：8，16，24，32，40，48

12的倍数：12，24，36，48

8和12的公倍数有：24，48

因为这个班同学在40人50人之间，所以这个班人数是48人。

答：这个班有48人。

本题考查公倍数，解答本题的关键就是根据8和12的公倍数找到这个班同学的人数。

29、（1）1月；（2）38万元；（3）715万元；（4）28.5万元

【解析】略

30、4.375平方米

【分析】求至少需要用布多少平方米，就相当于求除了底面之外的5个面的面积，根据长方体的表面积公式代入数据解答即可。

【详解】（0.75×1.6+0.5×1.6）×2+0.75×0.5

=4+0.375

=4.375（平方米）

答：至少需要用布4.375平方米。

本题是有关长方体计算的实际问题，一定要搞清所求的是几个面的面积和，知识点：长方体的表面积公式：S=（ab+ah+bh）×2。