
2023年四川省成都市数学中考真题含解析卷
展开2023年四川省成都市数学中考真题
A卷(共100分)
第I卷(选择题,共32分)
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1. 在,,,四个数中,最大的数是( )
A. 3 B. C. 0 D.
2. 2023年5月17日10时49分,我国在西昌卫星发射中心成功发射第五十六颗北斗导航卫星.北斗系统作为国家重要基础设施,深刻改变着人们的生产生活方式.目前,某地图软件调用的北斗卫星日定位量超亿次.将数据亿用科学记数法表示为( )
A. B. C. D.
3. 下列计算正确的是( )
A. B.
C. D.
4. 近年来,随着环境治理的不断深入,成都已构建起“青山绿道蓝网”生态格局.如今空气质量越来越好,杜甫那句“窗含西岭千秋雪”已成为市民阳台外一道靓丽的风景.下面是成都市今年三月份某五天的空气质量指数():,,,,,则这组数据的中位数是( )
A. B. C. D.
5. 如图,在中,对角线与相交于点,则下列结论一定正确的是( )
A B. C. D.
6. 为贯彻教育部《大中小学劳动教育指导纲要(试行)》文件精神,某学校积极开设种植类劳动教育课.某班决定每位学生随机抽取一张卡片来确定自己种植项目,老师提供6张背面完全相同的卡片,其中蔬菜类有4张,正面分别印有白菜、辣椒、豇豆、茄子图案;水果类有2张,正面分别印有草莓、西瓜图案,每个图案对应该种植项目.把这6张卡片背面朝上洗匀,小明随机抽取一张,他恰好抽中水果类卡片的概率是( )
A. B. C. D.
7. 《孙子算经》是中国古代重要的数学著作,是《算经十书》之一.书中记载了这样一个题目:今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?其大意是:用一根绳子去量一根长木,绳子还剩余尺;将绳子对折再量长木,长木还剩余尺.问木长多少尺?设木长尺,则可列方程为( )
A. B.
C. D.
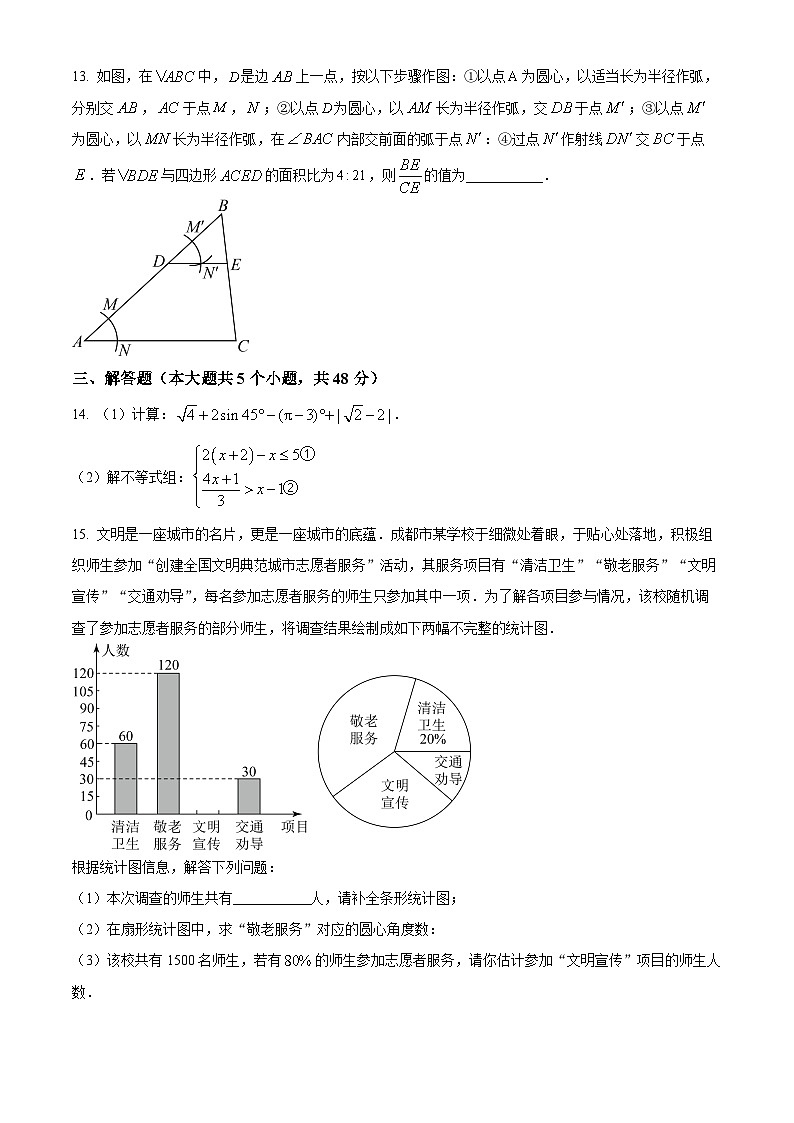
8. 如图,二次函数的图象与x轴交于,两点,下列说法正确的是( )
A. 抛物线的对称轴为直线 B. 抛物线的顶点坐标为
C. ,两点之间的距离为 D. 当时,的值随值的增大而增大
第Ⅱ卷(非选择题,共68分)
二、填空题(本大题共5个小题,每小题4分,共20分)
9. 因式分解:m2﹣3m=__________.
10. 若点都在反比例函数的图象上,则_______(填“”或“”).
11. 如图,已知,点B,E,C,F依次在同一条直线上.若,则的长为___________.
12. 在平面直角坐标系中,点关于y轴对称的点的坐标是___________.
13. 如图,在中,是边上一点,按以下步骤作图:①以点为圆心,以适当长为半径作弧,分别交,于点,;②以点为圆心,以长为半径作弧,交于点;③以点为圆心,以长为半径作弧,在内部交前面的弧于点:④过点作射线交于点.若与四边形的面积比为,则的值为___________.
三、解答题(本大题共5个小题,共48分)
14. (1)计算:.
(2)解不等式组:
15. 文明是一座城市的名片,更是一座城市的底蕴.成都市某学校于细微处着眼,于贴心处落地,积极组织师生参加“创建全国文明典范城市志愿者服务”活动,其服务项目有“清洁卫生”“敬老服务”“文明宣传”“交通劝导”,每名参加志愿者服务的师生只参加其中一项.为了解各项目参与情况,该校随机调查了参加志愿者服务的部分师生,将调查结果绘制成如下两幅不完整的统计图.
根据统计图信息,解答下列问题:
(1)本次调查的师生共有___________人,请补全条形统计图;
(2)在扇形统计图中,求“敬老服务”对应的圆心角度数:
(3)该校共有1500名师生,若有的师生参加志愿者服务,请你估计参加“文明宣传”项目的师生人数.
16. 为建设美好公园社区,增强民众生活幸福感,某社区服务中心在文化活动室墙外安装避阳篷,便于社区居民休憩.如图,在侧面示意图中,遮阳篷长为米,与水平面的夹角为,且靠墙端离地高为米,当太阳光线与地面的夹角为时,求阴影的长.(结果精确到米;参考数据:)
17. 如图,以的边为直径作,交边于点D,过点C作交于点E,连接.
(1)求证:;
(2)若,求和的长.
18. 如图,在平面直角坐标系中,直线与y轴交于点A,与反比例函数的图象的一个交点为,过点B作AB的垂线l.
(1)求点A的坐标及反比例函数的表达式;
(2)若点C在直线l上,且的面积为5,求点C的坐标;
(3)P是直线l上一点,连接PA,以P为位似中心画,使它与位似,相似比为m.若点D,E恰好都落在反比例函数图象上,求点P的坐标及m的值.
B卷(共50分)
一、填空题(本大题共5个小题,每小题4分,共20分)
19. 若,则代数式,的值为___________.
20. 一个几何体由几个大小相同小立方块搭成,它的主视图和俯视图如图所示,则搭成这个几何体的小立方块最多有___________个.
21. 为传承非遗文化,讲好中国故事,某地准备在一个场馆进行川剧演出.该场馆底面为一个圆形,如图所示,其半径是10米,从A到B有一笔直的栏杆,圆心O到栏杆的距离是5米,观众在阴影区域里观看演出,如果每平方米可以坐3名观众,那么最多可容纳___________名观众同时观看演出.(取3.14,取1.73)
22. 如图,在中,,平分交于点,过作交于点,将沿折叠得到,交于点.若,则__________.
23. 定义:如果一个正整数能表示为两个正整数,的平方差,且,则称这个正整数为“智慧优数”.例如,,16就是一个智慧优数,可以利用进行研究.若将智慧优数从小到大排列,则第3个智慧优数是________;第23个智慧优数是________.
二、解答题(本大题共3个小题,共30分)
24. 年月日至月日,第届世界大学生运动会将成都举行.“当好东道主,热情迎嘉宾”,成都某知名小吃店计划购买,两种食材制作小吃.已知购买千克种食材和千克种食材共需元,购买千克种食材和千克种食材共需元.
(1)求,两种食材的单价;
(2)该小吃店计划购买两种食材共千克,其中购买种食材千克数不少于种食材千克数的倍,当,两种食材分别购买多少千克时,总费用最少?并求出最少总费用.
25. 如图,在平面直角坐标系中,已知抛物线经过点,与y轴交于点,直线与抛物线交于B,C两点.
(1)求抛物线的函数表达式;
(2)若是以为腰的等腰三角形,求点B的坐标;
(3)过点作y轴的垂线,交直线AB于点D,交直线AC于点E.试探究:是否存在常数m,使得始终成立?若存在,求出m的值;若不存在,请说明理由.
26. 探究式学习是新课程倡导的重要学习方式,某兴趣小组拟做以下探究.
在中,,D是边上一点,且(n为正整数),E是边上动点,过点D作的垂线交直线于点F.
【初步感知】
(1)如图1,当时,兴趣小组探究得出结论:,请写出证明过程.
【深入探究】
(2)①如图2,当,且点F在线段上时,试探究线段之间的数量关系,请写出结论并证明;
②请通过类比、归纳、猜想,探究出线段之间数量关系的一般结论(直接写出结论,不必证明)
【拓展运用】
(3) 如图3,连接,设的中点为M.若,求点E从点A运动到点C的过程中,点M运动的路径长(用含n的代数式表示).
2023年四川省成都市数学中考真题
A卷(共100分)
第I卷(选择题,共32分)
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1. 在,,,四个数中,最大的数是( )
A. 3 B. C. 0 D.
【答案】A
【解析】
【分析】根据有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小,据此判断即可.
【详解】解:根据有理数比较大小方法,可得
,
∴最大的数是:3;
故选:A.
【点睛】此题主要考查了有理数大小比较的方法,要熟练掌握,解答此题的关键是要明确:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.
2. 2023年5月17日10时49分,我国在西昌卫星发射中心成功发射第五十六颗北斗导航卫星.北斗系统作为国家重要基础设施,深刻改变着人们的生产生活方式.目前,某地图软件调用的北斗卫星日定位量超亿次.将数据亿用科学记数法表示为( )
A. B. C. D.
【答案】D
【解析】
【分析】用科学记数法表示较大的数时,一般形式为,其中,为整数.
【详解】解:亿.
故选:D.
【点睛】本题考查了科学记数法,科学记数法的表示形式为的形式,其中,为整数.确定的值时,要看把原来的数,变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.当原数绝对值时,是正数;当原数的绝对值时,是负数,确定与的值是解题的关键.
3. 下列计算正确的是( )
A. B.
C. D.
【答案】C
【解析】
【分析】分别根据积的乘方、合并同类项、乘法公式逐项求解判断即可.
【详解】解:A、,故原计算错误,不符合题意;
B、,故原计算错误,不符合题意;
C、,故原计算正确,符合题意;
D、,故原计算错误,不符合题意,
故选:C.
【点睛】本题考查积的乘方、合并同类项、乘法公式,熟记完全平方公式和平方差公式,正确判断是解答的关键.
4. 近年来,随着环境治理的不断深入,成都已构建起“青山绿道蓝网”生态格局.如今空气质量越来越好,杜甫那句“窗含西岭千秋雪”已成为市民阳台外一道靓丽的风景.下面是成都市今年三月份某五天的空气质量指数():,,,,,则这组数据的中位数是( )
A. B. C. D.
【答案】C
【解析】
【分析】将这组数据从小到大重新排列,再根据中位数的定义求解即可.
【详解】将这组数据从小到大重新排列为,,,,
∴这组数据的中位数为,
故选:C.
【点睛】本题主要考查中位数,将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
5. 如图,在中,对角线与相交于点,则下列结论一定正确的是( )
A. B. C. D.
【答案】B
【解析】
【分析】根据平行四边形的性质逐项分析判断即可求解.
【详解】∵四边形是平行四边形,对角线与相交于点,
A. ,不一定成立,故该选项不正确,不符合题意;
B. ,故该选项正确,符合题意;
C. ,不一定成立,故该选项不正确,不符合题意;
D. ,不一定成立,故该选项不正确,不符合题意;
故选:B.
【点睛】本题考查了平行四边形的性质,熟练掌握平行四边形的性质是解题的关键.
6. 为贯彻教育部《大中小学劳动教育指导纲要(试行)》文件精神,某学校积极开设种植类劳动教育课.某班决定每位学生随机抽取一张卡片来确定自己的种植项目,老师提供6张背面完全相同的卡片,其中蔬菜类有4张,正面分别印有白菜、辣椒、豇豆、茄子图案;水果类有2张,正面分别印有草莓、西瓜图案,每个图案对应该种植项目.把这6张卡片背面朝上洗匀,小明随机抽取一张,他恰好抽中水果类卡片的概率是( )
A. B. C. D.
【答案】B
【解析】
【分析】根据概率公式求解即可.
【详解】解:由题意,随机抽取一张,共有6种等可能的结果,其中恰好抽中水果类卡片的有2种,
∴小明随机抽取一张,他恰好抽中水果类卡片的概率是,
故选:B.
【点睛】本题考查求简单事件的概率,关键是熟知求概率公式:所求情况数与总情况数之比.
7. 《孙子算经》是中国古代重要的数学著作,是《算经十书》之一.书中记载了这样一个题目:今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?其大意是:用一根绳子去量一根长木,绳子还剩余尺;将绳子对折再量长木,长木还剩余尺.问木长多少尺?设木长尺,则可列方程为( )
A. B.
C. D.
【答案】A
【解析】
【分析】设木长尺,根据题意“用一根绳子去量一根长木,绳子还剩余尺;将绳子对折再量长木,长木还剩余尺”,列出一元一次方程即可求解.
【详解】解:设木长尺,根据题意得,
,
故选:A
【点睛】本题考查了一元一次方程的应用,根据题意列出方程是解题的关键.
8. 如图,二次函数的图象与x轴交于,两点,下列说法正确的是( )
A. 抛物线的对称轴为直线 B. 抛物线的顶点坐标为
C. ,两点之间的距离为 D. 当时,的值随值的增大而增大
【答案】C
【解析】
【分析】待定系数法求得二次函数解析式,进而逐项分析判断即可求解.
【详解】解:∵二次函数的图象与x轴交于,两点,
∴
∴
∴二次函数解析式为,对称轴为直线,顶点坐标为,故A,B选项不正确,不符合题意;
∵,抛物线开口向上,当时,的值随值的增大而减小,故D选项不正确,不符合题意;
当时,
即
∴,
∴,故C选项正确,符合题意;
故选:C.
【点睛】本题考查了二次函数的性质,待定系数法求二次函数解析式,抛物线与坐标轴的交点,熟练掌握二次函数的性质是解题的关键.
第Ⅱ卷(非选择题,共68分)
二、填空题(本大题共5个小题,每小题4分,共20分)
9. 因式分解:m2﹣3m=__________.
【答案】
【解析】
【分析】题中二项式中各项都含有公因式,利用提公因式法因式分解即可得到答案.
【详解】解:,
故答案为:.
【点睛】本题考查整式运算中的因式分解,熟练掌握因式分解的方法技巧是解决问题的关键.
10. 若点都在反比例函数的图象上,则_______(填“”或“”).
【答案】
【解析】
【分析】根据题意求得,,进而即可求解.
【详解】解:∵点都在反比例函数的图象上,
∴,,
∵,
∴,
故答案为:.
【点睛】本题考查了比较反比例函数值,熟练掌握反比例函数的性质是解题的关键.
11. 如图,已知,点B,E,C,F依次在同一条直线上.若,则的长为___________.
【答案】3
【解析】
【分析】利用平移性质求解即可.
【详解】解:由平移性质得:,
∴,
故答案为:3.
【点睛】本题考查平移性质,熟练掌握平移性质是解答的关键.
12. 在平面直角坐标系中,点关于y轴对称的点的坐标是___________.
【答案】
【解析】
【分析】根据关于y轴对称的点,纵坐标相同,横坐标互为相反进行求解即可.
【详解】解:在平面直角坐标系中,点关于y轴对称的点的坐标是,
故答案为:.
【点睛】本题主要考查了坐标与图形变化—轴对称,解决本题的关键是掌握关于y轴对称的点,纵坐标相同,横坐标互为相反数.
13. 如图,在中,是边上一点,按以下步骤作图:①以点为圆心,以适当长为半径作弧,分别交,于点,;②以点为圆心,以长为半径作弧,交于点;③以点为圆心,以长为半径作弧,在内部交前面的弧于点:④过点作射线交于点.若与四边形的面积比为,则的值为___________.
【答案】
【解析】
【分析】根据作图可得,然后得出,可证明,进而根据相似三角形的性质即可求解.
【详解】解:根据作图可得,
∴,
∴,
∵与四边形的面积比为,
∴
∴
∴,
故答案为:.
【点睛】本题考查了作一个角等于已知角,相似三角形的性质与判定,熟练掌握基本作图与相似三角形的性质与判定是解题的关键.
三、解答题(本大题共5个小题,共48分)
14. (1)计算:.
(2)解不等式组:
【答案】(1)3;(2)
【解析】
【分析】(1)先计算算术平方根、特殊角的三角函数值、零指数幂和绝对值,再加减运算即可求解;
(2)先求得每个不等式的解集,再求得它们的公共部分即可求解;
【详解】解:(1)
;
(2)解不等式①,得,
解不等式②,得,
∴不等式组的解集为.
【点睛】本题主要考查实数的混合运算和解一元一次不等式组,涉及到特殊角的三角函数值、零指数幂、绝对值、二次根式的加减等知识,熟练掌握相关运算法则并正确求解是解答的关键.
15. 文明是一座城市的名片,更是一座城市的底蕴.成都市某学校于细微处着眼,于贴心处落地,积极组织师生参加“创建全国文明典范城市志愿者服务”活动,其服务项目有“清洁卫生”“敬老服务”“文明宣传”“交通劝导”,每名参加志愿者服务的师生只参加其中一项.为了解各项目参与情况,该校随机调查了参加志愿者服务的部分师生,将调查结果绘制成如下两幅不完整的统计图.
根据统计图信息,解答下列问题:
(1)本次调查的师生共有___________人,请补全条形统计图;
(2)在扇形统计图中,求“敬老服务”对应的圆心角度数:
(3)该校共有1500名师生,若有的师生参加志愿者服务,请你估计参加“文明宣传”项目的师生人数.
【答案】(1),图见解析;
(2);
(3)人;
【解析】
【分析】(1)根据“清洁卫生”的人数除以占比即可得出样本的容量,进而求“文明宣传”的人数,补全统计图;
(2)根据“敬老服务”的占比乘以即可求解;
(3)用样本估计总体,用乘以再乘以“文明宣传”的 比即可求解.
【小问1详解】
解:依题意,本次调查的师生共有人,
∴“文明宣传”的人数为(人)
补全统计图,如图所示,
故答案为:.
【小问2详解】
在扇形统计图中,求“敬老服务”对应的圆心角度数为,
【小问3详解】
估计参加“文明宣传”项目的师生人数为(人).
【点睛】本题主要考查了条形统计图和扇形统计图的综合运用,样本估计总体,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
16. 为建设美好公园社区,增强民众生活幸福感,某社区服务中心在文化活动室墙外安装避阳篷,便于社区居民休憩.如图,在侧面示意图中,遮阳篷长为米,与水平面的夹角为,且靠墙端离地高为米,当太阳光线与地面的夹角为时,求阴影的长.(结果精确到米;参考数据:)
【答案】米
【解析】
【分析】过点作于点,于点,则四边形是矩形,在中,求得,进而求得,根据,即可求解.
【详解】解:如图所示,过点作于点,于点,则四边形是矩形,
依题意, ,(米)
在中,(米),(米),则(米)
∵(米)
∴(米)
∵,
∴(米)
∴(米).
【点睛】本题考查了解直角三角形的应用,添加辅助线构造直角三角形是解题的关键.
17. 如图,以的边为直径作,交边于点D,过点C作交于点E,连接.
(1)求证:;
(2)若,求和的长.
【答案】(1)见解析 (2),
【解析】
【分析】(1)根据,得到,再根据同弦所对的圆周角相等,得到,可证明是等腰三角形,即可解答;
(2)根据直径所对的圆周角为直角,得到,设,根据勾股定理列方程,解得x的值,即可求出;过点作的垂线段,交的延长线于点F,证明,求出的长,根据勾股定理即可解出的长.
【小问1详解】
证明:,
,
,
,
,
;
【小问2详解】
解:设,
是的直径,
,
,
,即,
根据(1)中的结论,可得,
根据勾股定理,可得,即,
解得,(舍去),
,,
根据勾股定理,可得;
如图,过点作的垂线段,交的延长线于点F,
,
,
(1)中已证明,
,
,
,即,
,,,
,
,
,
设,则,
,
可得方程,解得,
,,
根据勾股定理,可得.
【点睛】本题考查了圆周角定理,等腰三角形的判定和性质,平行线的性质,勾股定理,正切的概念,利用等量代换证明相关角相等是解题的关键.
18. 如图,在平面直角坐标系中,直线与y轴交于点A,与反比例函数的图象的一个交点为,过点B作AB的垂线l.
(1)求点A的坐标及反比例函数的表达式;
(2)若点C在直线l上,且的面积为5,求点C的坐标;
(3)P是直线l上一点,连接PA,以P为位似中心画,使它与位似,相似比为m.若点D,E恰好都落在反比例函数图象上,求点P的坐标及m的值.
【答案】(1)点A的坐标为,反比例函数的表达式为;
(2)点C的坐标为或
(3)点P的坐标为;m的值为3
【解析】
【分析】(1)利用直线解析式可的点C的坐标,将点代入可得a的值,再将点代入反比例函数解析式可得k的值,从而得解;
(2)设直线l于y轴交于点M,由点B的坐标和直线l是的垂线先求出点M的坐标,再用待定系数法求直线l的解析式,C点坐标为,根据(分别代表点B与点C的横坐标)可得点C的横坐标,从而得解;
(3) 位似图形的对应点与位似中心三点共线可知点B的对应点也在直线l上,不妨设为点E,则点A的对应点是点D,直线l与双曲线的解析式联立方程组得到,由得到,继而得到直线与直线的解析式中的一次项系数相等,设直线的解析式是:,将代入求得的解析式是:,再将直线与双曲线的解析式联立求得,再用待定系数法求出的解析式是,利用直线的解析式与直线l的解析式联立求得点P的坐标为,再用两点间的距离公式得到,从而求得.
【小问1详解】
解:令,则
∴点A的坐标为,
将点代入得:
解得:
∴
将点代入得:
解得:
∴反比例函数的表达式为;
【小问2详解】
解:设直线l于y轴交于点M,直线与x轴得交点为N,
令解得:
∴,
∴,
又∵,
∴
∵,
∴
又∵直线l是的垂线即,,
∴,
∴
设直线l得解析式是:,
将点,点代入得:
解得:
∴直线l的解析式是:,
设点C的坐标是
∵,(分别代表点B与点C的横坐标)
解得: 或6,
当时,;
当时,,
∴点C坐标为或
【小问3详解】
∵位似图形的对应点与位似中心三点共线,
∴点B的对应点也在直线l上,不妨设为点E,则点A的对应点是点D,
∴点E是直线l与双曲线的另一个交点,
将直线l与双曲线的解析式联立得:
解得:或
∴
画出图形如下:
又∵
∴
∴
∴直线与直线的解析式中的一次项系数相等,
设直线的解析式是:
将点代入得:
解得:
∴直线的解析式是:
∵点D也在双曲线上,
∴点D是直线与双曲线的另一个交点,
将直线与双曲线的解析式联立得:
解得:或
∴
设直线的解析式是:
将点,代入得:
解得:
∴直线的解析式是:,
又将直线的解析式与直线l的解析式联立得:
解得:
∴点P的坐标为
∴
∴
【点睛】本题考查直线与坐标轴的交点,求反比例函数解析式,反比例函数的图象与性质,反比例函数综合几何问题,三角形的面积公式,位似的性质等知识,综合性大,利用联立方程组求交点和掌握位似的性质是解题的关键.
B卷(共50分)
一、填空题(本大题共5个小题,每小题4分,共20分)
19. 若,则代数式,的值为___________.
【答案】
【解析】
【分析】根据分式的化简法则,将代数式化简可得,再将变形,即可得到答案.
【详解】解:,
,
,
,
,
,
,
故原式的值为,
故答案为:.
【点睛】本题考查了分式的化简法则,整式的整体代入,熟练对代数式进行化简是解题的关键.
20. 一个几何体由几个大小相同的小立方块搭成,它的主视图和俯视图如图所示,则搭成这个几何体的小立方块最多有___________个.
【答案】
【解析】
【分析】根据主视图和俯视图可得第一列最多2个,第二列最多1个小正方形,即可求解.
【详解】解:根据主视图和俯视图可得第一列最多2个,第二列最多1个小正方形,如图所示,
∴搭成这个几何体的小立方块最多有,
故答案为:.
【点睛】本题考查了三视图,熟练掌握三视图的定义是解题的关键.
21. 为传承非遗文化,讲好中国故事,某地准备在一个场馆进行川剧演出.该场馆底面为一个圆形,如图所示,其半径是10米,从A到B有一笔直的栏杆,圆心O到栏杆的距离是5米,观众在阴影区域里观看演出,如果每平方米可以坐3名观众,那么最多可容纳___________名观众同时观看演出.(取3.14,取1.73)
【答案】184
【解析】
【分析】过点O作的垂线段,交于点,根据直角三角形的边长关系求出的角度,阴影面积即为扇形的面积减去三角形的面积,随机可以求出容纳观众的数量.
【详解】解:如图,过点O作的垂线段,交于点,
圆心O到栏杆的距离是5米,
米,
,
,米,
,
,
,
可容纳观众
阴影部分面积(人),
最多可容纳184名观众同时观看演出,
故答案为:184.
【点睛】本题考查了弓形的面积,根据特殊角三角函数值求角的度数,熟知扇形面积公式是解题的关键.
22. 如图,在中,,平分交于点,过作交于点,将沿折叠得到,交于点.若,则__________.
【答案】
【解析】
【分析】过点作于,证明,得出,根据,得,设,,则,则,在中,,在中,,则,解方程求得,则,,勾股定理求得,根据正切的定义,即可求解.
【详解】解:如图所示,过点作于,
∵平分交于点,
∴,
∴
∴
∵折叠,
∴,
∴,
又∵
∴
∴
∴
∵,,则,
∴
∴,,
∵
设,,则,则,
∵
∴
中,
在中,
∴
即
解得:
∴,
则
∴
故答案为:.
【点睛】本题考查了求正切,折叠的性质,勾股定理,平行线分线段成比例,相似三角形的性质与判定,熟练掌握以上知识是解题的关键.
23. 定义:如果一个正整数能表示为两个正整数,的平方差,且,则称这个正整数为“智慧优数”.例如,,16就是一个智慧优数,可以利用进行研究.若将智慧优数从小到大排列,则第3个智慧优数是________;第23个智慧优数是________.
【答案】 ①. ②.
【解析】
【分析】根据新定义,列举出前几个智慧优数,找到规律,进而即可求解.
【详解】解:依题意, 当,,则第1个一个智慧优数为
当,,则第2个智慧优数为
当,,则第3个智慧优数为,
当,,则第5个智慧优数为
当,,则第6个智慧优数为
当,,则第7个智慧优数为
……
时有4个智慧优数,同理时有个,时有6个,
第22个智慧优数,当时,,第22个智慧优数为,
第23个智慧优数为时,,
故答案为:,.
【点睛】本题考查了新定义,平方差公式的应用,找到规律是解题的关键.
二、解答题(本大题共3个小题,共30分)
24. 年月日至月日,第届世界大学生运动会将在成都举行.“当好东道主,热情迎嘉宾”,成都某知名小吃店计划购买,两种食材制作小吃.已知购买千克种食材和千克种食材共需元,购买千克种食材和千克种食材共需元.
(1)求,两种食材的单价;
(2)该小吃店计划购买两种食材共千克,其中购买种食材千克数不少于种食材千克数的倍,当,两种食材分别购买多少千克时,总费用最少?并求出最少总费用.
【答案】(1)种食材单价是每千克元,种食材单价是每千克元
(2)种食材购买千克,种食材购买千克时,总费用最少,为元
【解析】
【分析】(1)设种食材的单价为元,种食材的单价为元,根据题意列出二元一次方程组,解方程组即可求解;
(2)设种食材购买千克,则种食材购买千克,根据题意列出不等式,得出,进而设总费用为元,根据题意,,根据一次函数的性质即可求解.
【小问1详解】
解:设种食材的单价为元,种食材的单价为元,根据题意得,
,
解得:,
答:种食材的单价为元,种食材的单价为元;
【小问2详解】
解:设种食材购买千克,则种食材购买千克,根据题意,
解得:,
设总费用为元,根据题意,
∵,随的增大而增大,
∴当时,最小,
∴最少总费用为(元)
【点睛】本题考查了二元一次方程组的应用,一元一次不等式的应用,一次函数的应用,根据题意列出方程组,不等式以及一次函数关系式是解题的关键.
25. 如图,在平面直角坐标系中,已知抛物线经过点,与y轴交于点,直线与抛物线交于B,C两点.
(1)求抛物线的函数表达式;
(2)若是以为腰的等腰三角形,求点B的坐标;
(3)过点作y轴的垂线,交直线AB于点D,交直线AC于点E.试探究:是否存在常数m,使得始终成立?若存在,求出m的值;若不存在,请说明理由.
【答案】(1)
(2)点B的坐标为或或
(3)存在,m的值为2或
【解析】
【分析】(1)利用待定系数法求解即可;
(2)设,分和两种情况,分别根据等腰三角形性质和两点坐标距离公式列方程求解即可;
(3)先根据题意画出图形,设抛物线与直线的交点坐标为,,联立抛物线和直线解析式,根据根与系数关系得到,,利用待定系数法分别求得直线、的表达式为得到, ,过E作轴于Q,过D作轴于N,证明得到,整理可得到,进而求解即可.
【小问1详解】
解:∵抛物线经过点,与y轴交于点,
∴,解得,
∴抛物线的函数表达式为;
【小问2详解】
解:设,
根据题意,是以为腰的等腰三角形,有两种情况:
当时,点B和点P关于y轴对称,
∵,∴;
当时,则,
∴,
整理,得,
解得,,
当时,,则,
当时,,则,
综上,满足题意的点B的坐标为或或;
【小问3详解】
解:存在常数m,使得.
根据题意,画出图形如下图,
设抛物线与直线的交点坐标为,,
由得,
∴,;
设直线的表达式为,
则,解得,
∴直线的表达式为,
令,由得,
∴,
同理,可得直线的表达式为,则,
过E作轴于Q,过D作轴于N,
则,,,,
若,则,
∴,
∴,
∴,
∴,
则,
整理,得,
即,
将,代入,得,
即,则或,
解得,,
综上,存在常数m,使得,m的值为2或.
【点睛】本题是二次函数的综合题,主要考查了待定系数法求函数的解析式、等腰三角形的性质、一元二次方程根与系数关系、相似三角形的判定与性质、解一元二次方程、坐标与图形等知识,综合性强,难度较大,熟练掌握相关知识的联系与运用,添加辅助线构造相似三角形,并利用数形结合和分类讨论思想解决问题是解答的关键.
26. 探究式学习是新课程倡导的重要学习方式,某兴趣小组拟做以下探究.
在中,,D是边上一点,且(n为正整数),E是边上的动点,过点D作的垂线交直线于点F.
【初步感知】
(1)如图1,当时,兴趣小组探究得出结论:,请写出证明过程.
【深入探究】
(2)①如图2,当,且点F在线段上时,试探究线段之间的数量关系,请写出结论并证明;
②请通过类比、归纳、猜想,探究出线段之间数量关系的一般结论(直接写出结论,不必证明)
【拓展运用】
(3)如图3,连接,设的中点为M.若,求点E从点A运动到点C的过程中,点M运动的路径长(用含n的代数式表示).
【答案】(1)见解析 (2)①,证明过程略;②当点F在射线上时,,当点F在延长线上时,
(3)
【解析】
【分析】(1)连接,当时,,即,证明,从而得到即可解答;
(2)①过的中点作的平行线,交于点,交于点,当时,,根据,可得是等腰直角三角形,,根据(1)中结论可得,再根据,,即可得到;
②分类讨论,即当点F在射线上时;当点F在延长线上时,画出图形,根据①中的原理即可解答;
(3)如图,当与重合时,取的中点,当与重合时,取的中点,可得的轨迹长度即为的长度,可利用建系的方法表示出的坐标,再利用中点公式求出,最后利用勾股定理即可求出的长度.
【小问1详解】
证明:如图,连接,
当时,,即,
,
,,,
,,即,
,
,
在与中,
,
,
,
;
【小问2详解】
①
证明:如图,过的中点作的平行线,交于点,交于点,
当时,,即,
是的中点,
,,
,
,,
,
是等腰直角三角形,且,
,
根据(1)中的结论可得,
;
故线段之间的数量关系为;
②解:当点F在射线上时,
如图,在上取一点使得,过作的平行线,交于点,交于点,
同①,可得,
,,
,,
同①可得,
,
即线段之间数量关系为;
当点F在延长线上时,
如图,在上取一点使得,过作的平行线,交于点,交于点,连接
同(1)中原理,可证明,
可得,
,,
,,
同①可得,
即线段之间数量关系为,
综上所述,当点F射线上时,;当点F在延长线上时,;
【小问3详解】
解:如图,当与重合时,取的中点,当与重合时,取的中点,可得的轨迹长度即为的长度,
如图,以点为原点,为轴,为轴建立平面直角坐标系,过点作的垂线段,交于点,过点作的垂线段,交于点,
,
,,
,
,
,
,
是的中点,
,
,
,
,
根据(2)中的结论,
,
,
,
,
,
.
【点睛】本题考查了等腰三角形的性质,全等三角形的判定及性质,相似三角形的判定及性质,平行线的性质,正确地画出图形,作出辅助线,找对边之间的关系是解题的关键.
2023年四川省成都市数学中考真题(含解析): 这是一份2023年四川省成都市数学中考真题(含解析),共34页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
精品解析:2022年四川省成都市中考数学真题(解析版): 这是一份精品解析:2022年四川省成都市中考数学真题(解析版),共32页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022年四川省成都市中考数学真题(解析版): 这是一份2022年四川省成都市中考数学真题(解析版),共32页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












