河南省洛阳市创新发展联盟2022-2023学年高二下学期5月阶段性检测+数学+Word版含解析

2022~2023学年下学期创新发展联盟高二阶段检测

数  学

注意事项：

1.答题前，考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

4.本试卷主要考试内容：人教A版选择性必修一、二、三。

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 若一个等差数列的前7项和为21，则该等差数列的第4项为

A.2                   B.3                  C.4                D.5

2. 若 则D(T)=

A.3                  B.4                                  

3. 已知点P在圆 上，则点P到x轴的距离的最大值为

A.2                  B.3                  C.                 

4. 某地区内猫的寿命超过12岁的概率为p，超过16岁的概率为0.15，且一只寿命超过12岁的猫的寿命超过16岁的概率为从该地区内任选两只猫，则至少有一只寿命超过12岁的概率为

A.0.88                B.0.9                 C.0.96               D.0.99

5. 如图，某手链由10颗较小的珠子(每颗珠子相同)和11颗较大的珠子(每颗珠子均不相同)串成，若10颗小珠子必须相邻，大珠子的位置任意，则该手链不同的串法有

A. 种                                  种

C. 种                                种

6.    的展开式的常数项为

A.1                  B.121                 C.-119                D.-120

7. 已知是定义在R上的奇函数,的导函数为,若恒成立,则的解集为

A.[-π,+∞)            B.[π,十∞)                      D.[0,+∞)

8. 已知抛物线 直线与交于,两点,直线 与交于,两点,则||+2||的最小值为

二、选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.

9. 某社区医院工作人员在社区内开展了“如何护理患有黄疸的新生儿”的知识讲座，并向参与讲座的每人发放了一份相关的知识问卷.该讲座结束后，共收回问卷100份.据统计，这100份问卷的得分X(满分为100分)服从正态分布N(80，25)，下列说法正确的是

附:若XN(μ,σ²),    则 P(<X)=0.683, P()=0.954, P()

A.这100份问卷得分数据的平均数是80，标准差是5

B.这100份问卷中得分超过85分的约有16份

C.P(70<X<75)= P(85<X<90)

D.若在其他社区开展该知识讲座并发放知识问卷，得到的问卷得分数据也服从正态分布N(80,25)

10. 在三棱锥A-BCD中, , , 两两夹角均为且若G,M分别为线段AD，BC的中点，则

C.异面直线AC与DB所成角的正弦值为

D.异面直线AC与DB所成角的正弦值为

11. 已知等比数列{}的前n项积为 且T₅=T₆,则下列结论正确的是

A.

的公比为-

12. 已知函数 下列结论正确的是

A. 在上单调递增

B. 的最大值为1

C.当时,

D.若函数恰有2个零点,则的取值范围为(0,1)

三、填空题：本题共4小题，每小题5分，共20分.

13. 双曲线 的焦点到渐近线的距离为5，则该双曲线的渐近线方程为         ▲          .

14. 现有A，B两艘轮船同时到达码头等待卸货，A轮船至少需要3名卸货工人，B轮船至少需要4名卸货工人.若码头有8名工人可以挑选，且每名工人只能去一艘轮船卸货，则这两艘轮船卸货的人选共有     ▲      种不同的选法.

15. 一个装有水的圆柱形水杯水平放在桌面上，在杯中放入一个半径为1cm的球状物体后，水面高度为6cm，如图所示.已知该水杯的底面圆半径为3cm，若从t=0s时刻开始，该球状物体的半径以1cm/s的速度变长(在该球状物体膨胀的过程中，该球状物体不吸水，且始终处于水面下，杯中的水不会溢出)，则在t =2s时刻,水面上升的瞬时速度为      ▲      cm/s.

16. 已知数列满足记为坐标原点,则△OAB面积的最大值为         ▲         .

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

17. (10分)

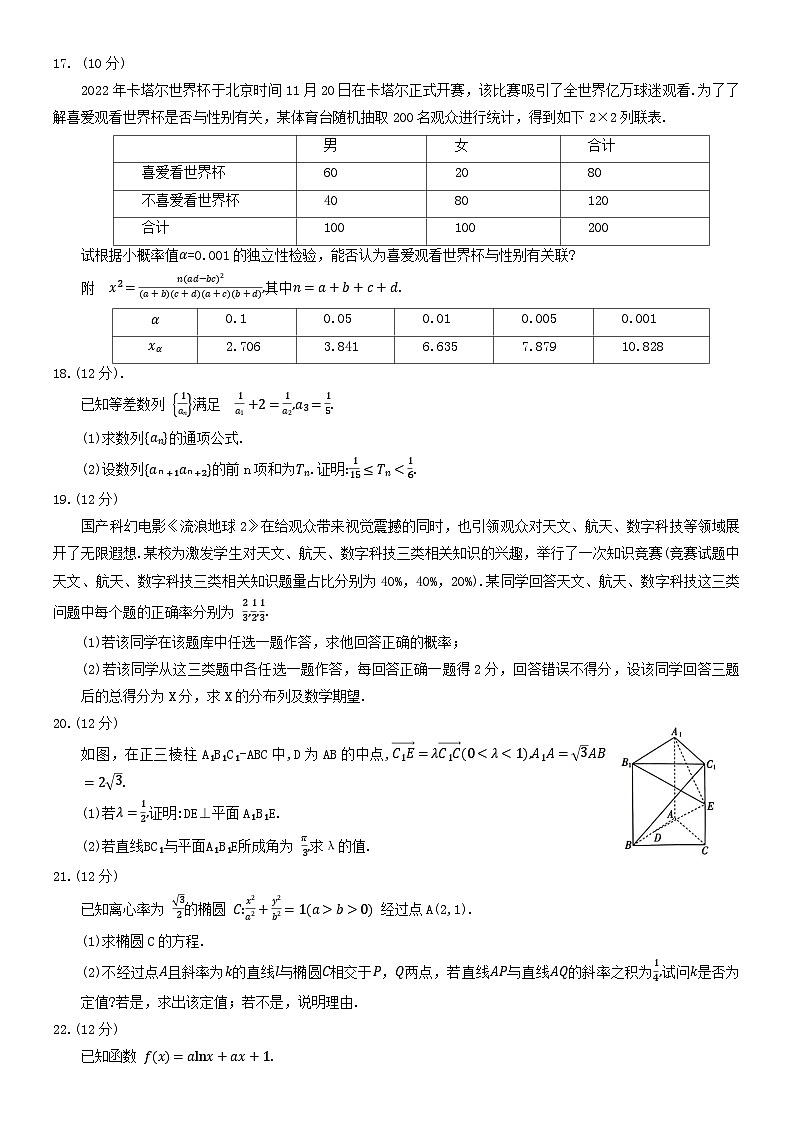
2022年卡塔尔世界杯于北京时间11月20日在卡塔尔正式开赛，该比赛吸引了全世界亿万球迷观看.为了了解喜爱观看世界杯是否与性别有关，某体育台随机抽取200名观众进行统计，得到如下2×2列联表.

试根据小概率值=0.001的独立性检验，能否认为喜爱观看世界杯与性别有关联?

附  其中

18.(12分).

已知等差数列 满足 

(1)求数列的通项公式.

(2)设数列的前n项和为.证明

19.(12分)

国产科幻电影《流浪地球2》在给观众带来视觉震撼的同时，也引领观众对天文、航天、数字科技等领域展开了无限遐想.某校为激发学生对天文、航天、数字科技三类相关知识的兴趣，举行了一次知识竞赛(竞赛试题中天文、航天、数字科技三类相关知识题量占比分别为40%，40%，20%).某同学回答天文、航天、数字科技这三类问题中每个题的正确率分别为

(1)若该同学在该题库中任选一题作答，求他回答正确的概率；

(2)若该同学从这三类题中各任选一题作答，每回答正确一题得2分，回答错误不得分，设该同学回答三题后的总得分为X分，求X的分布列及数学期望.

20.(12分)

如图，在正三棱柱A₁B₁C₁-ABC中,D为AB的中点,

(1)若证明:DE⊥平面A₁B₁E.

(2)若直线BC₁与平面A₁B₁E所成角为 求λ的值.

21.(12分)

已知离心率为 的椭圆 经过点A(2,1).

(1)求椭圆C的方程.

(2)不经过点且斜率为的直线与椭圆相交于，两点，若直线与直线的斜率之积为试问是否为定值?若是，求出该定值；若不是，说明理由.

22.(12分)

已知函数

(1)当时,求的图象在点(1,)处的切线方程;

(2)若不等式恒成立，求的取值集合.

2022~2023学年下学期创新发展联盟高二阶段检测

数学参考答案

1. B   因为第4项为该等差数列前7项的中间项，所以该等差数列的第4项为

2. C   因为 所以  

3. B   圆   即圆  易得点P到x轴的距离的最大值为2+1=3.

4. D   设A:猫的寿命超过12岁,B:猫的寿命超过16岁.依题意有P(A)=p,P(B)=P(B∩A)=0.15，则一只寿命超过12岁的猫的寿命超过16岁的概率 则p=0.9.从该地区内任选两只猫，则至少有一只寿命超过12岁的概率为  1-( 1 -0.9)²=0.99.

5. B   将10颗小珠子看成一个整体，不同的串法有  种.

6. C   因为 所以    的展开式的常数项为

7. D   令函数,则

因为所以.是增函数.

因为是奇函数,所以=0,)=-0=0,

所以的解集为[0,+∞),即≥的解集为[0,+∞).

8. A 设A,联立   得x²-4kx-4=0,则,因为直线经过C的焦点,所以，同理可得所以  +12,当且仅当时，等号成立.

9. ABC 由题意得,这100份问卷得分数据的平均数是80,标准差是5,A正确. P(X>85)= 所以这100份问卷中得分超过85分的约有16份，B 正确. P(70<X<75)=P(85<X<90)C正确。同一份

   问卷发到不同社区，得到的数据不一定相同，D错误.

10. BC   不妨设   则

因为 以 所以异面直线AC与DB所成角的正弦值为  

11. ABD   因为T₅=T₆,所以 a₆=1,A正确.

因为 a₆=a₁q⁵,所以   解得  正确.

 C 错误.

因  

所以   成立，D正确.

12.  BCD   的定义域为(0,+) 所以当0<x<1时, 单调递增，当x>1时单调递减,则=1,A 错误，B正确.

令    则 因为x∈(0,1),所以,为(0,1)上的增函数,则,即,C正确.

当m>1或m≤0时,g(x)没有零点.当m=1时,g(x)只有1个零点.当0<m<1时，令f(x)=t,方程f(f(x))-m=0的两个解为t₁,t₂,t₁∈(0,1),t₂∈(1,+∞),t₁=f(x)有2个不同的实根，t₂=f(x)没有实数根，故函数      g(x)=f(f(x))-m恰有2个零点时,m的取值范围为(0,1),D正确.

(或 依题意可得则该双曲线的渐近线方程为y=

14.406   若A轮船选择3名工人卸货,则有   种选法；若A轮船选择4名工人卸货，则有     种选法.故这两艘轮船卸货的人选共有336+70=406种不同的选法.

15.4   杯中水的体积为   设在该过程中水面高度为h，则π×3²×   即   令函数    则 故在t=2s时刻，

水面上升的瞬时速度为4 cm/s.

16.4   因为 所以    即

因为 =4,  所以是以4为首项为公比的等比数列， 所以     因为所以  

令函数     则.

当n≥1时,f(n+1)-f(n)≤0,所以f(1)=f(2),且f(n)在[2,+∞)上单调递减.

 ，故△OAB面积的最大值为4.

17.解:零假设为H₀:喜爱观看世界杯与性别无关联.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分

根据列表中的数据，经计算得到…………………6分

因为   ……………………………………………………………8分

根据小概率值=0.001的独立性检验，推断H₀不成立，即认为喜爱观看世界杯与性别有关联………………………………………………………………………………10分

18.(1)解:设数列  的公差为d，

则     …………………………………………………………………2分

所以    ………………………………………………………4分

故       …………………………………………………………………5分

(2)证明:    ……………………………7分

………………………………………………………………………………10分

因为函数  在(0,+∞)上单调递增,

所以  

故     …………………………………………………………………12分

19.解：(1)设所选的题目为天文、航天、数字科技相关知识的题目分别为事件A₁，A₂，A₃，所选

的题目回答正确为事件B，则 P(B)=P(A₁)P(B|A₁)+P(A₂)P(B|A₂)+P(A₃)P(B|A₃)

   …………………………………………………4分

(2)X的可能取值为0,2,4,6,………………………………………………………………5分

   …………………………………………6分

  ………………………………………………………………………………7分

   ，…………8分

   …………………………………………………………9分

则X的分布列为

…………………………………………………………………………………10分

    …………………………………………12分

20.(1)证明:取A₁B₁的中点F,连接EF,DF,DC,FC₁.

由题意得    

所以    DE²+EF²=DF², 则DE⊥EF.…………………………………………………2分

因为 A₁B₁⊥C₁F,A₁B₁⊥DF,所以A₁B₁⊥平面DCC₁F,所以DE⊥A₁B₁………………4分

因为A₁B₁∩EF=F,所以DE⊥平面A₁B₁E.………………………………………………5分

(2)解：以D为坐标原点， DB,DC,DF 的方向分别为x轴，y轴，z轴的正方向，建立空间直角坐标系，则              ………………………………………………6分

设 …………………………7分

设平面A₁B₁E的法向量为n=(x,y,z),

则  

取  则      ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9分

设直线BC₁与平面A₁B₁E所成的角为θ，

所以      ⋯⋯⋯⋯⋯⋯⋯10分

化简得 解得     或       ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯11分

当  时，点E与点C₁重合，此时λ=0，不符合题意.

所以  即λ的值为    …………………………………………………12分

21.解:(1)由题可知      ………………………………………………………2分

解得     故椭圆C的方程为     ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分

(2)设直线l的方程为y=kx+m,P(x₁,y₁),Q(x₂,y₂),

联立方程组      整理得( 1+4k²)x²+8kmx+4m²-8=0,              ……………………5分

则 △=64k²m²-(4+16k²)(4m²-8)=128k²-16m²+32>0,

  ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分

  …………………8分

整理得  4k²+2km+m-1=(2k+1)(m+2k-1)=0.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10分

因为不经过点A,所以m+2k-1≠0,所以2k+1=0,即     ……………………11分

故k为定值，且该定值为 ……………………………………………………12分

22.解:(1)当a=1时,f(x)=lnx+x+1,f(1)=2.                     ………………………………………1分

     …………………………………………………………3分

故f(x)的图象在点(1,f(1))处的切线方程为y=2(x-1)+2,即y=2x………………4分

(2)解法一：由题意可得   恒成立.

令函数   

则    ……………………5分

①当a<0时,   恒成立，此时g(x)单调递增，

g(x)的值域为R,不符合题意.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分

②当a=0时,则   不符合题意.………………………………………7分

③当a>0时,令   可得      即   

令函数   则    

所以   在(0,十∞)上单调递增…………………………………………………8分

设存在x₀∈(0,+∞),使得  两边同时取对数可得   x₀+ln x₀=ln a,

则当0<x< 时，  当x>x₀时,  

所以当x=x₀时,  

故只需a-alna-1≥0即可.……………………………………………………………10分

令函数φ(a)=a-aln a-1,则

由  可得0<a<1,由  可得a>1,

所以φ(a)在(0,1)上单调递增,在(1,+∞)上单调递减,

 即φ(a)=a-aln a-1≤0.……………………………………………11分

故a-aln a-1≥0只有唯一解,即a=1.

综上,a的取值集合为{1}…………………………………………………………………12分

解法二：由题意可得恒成立………………………………………6分

令  ,即t-aln t-1≥0.……………………………………………………………7分

令函数g(t)=t-aln t-1.

g(1)=0,要使g(t)≥0恒成立,则t=1是g(t)的极小值点………………………………9分

  解得a=1.……………………………………………11分

经检验，a=1符合题意.

综上,a的取值集合为{1}…………………………………………………………………1