安徽省2022-2023学年高三下学期第三次模拟考试文科数学试卷（含解析）

这是一份安徽省2022-2023学年高三下学期第三次模拟考试文科数学试卷（含解析），共20页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
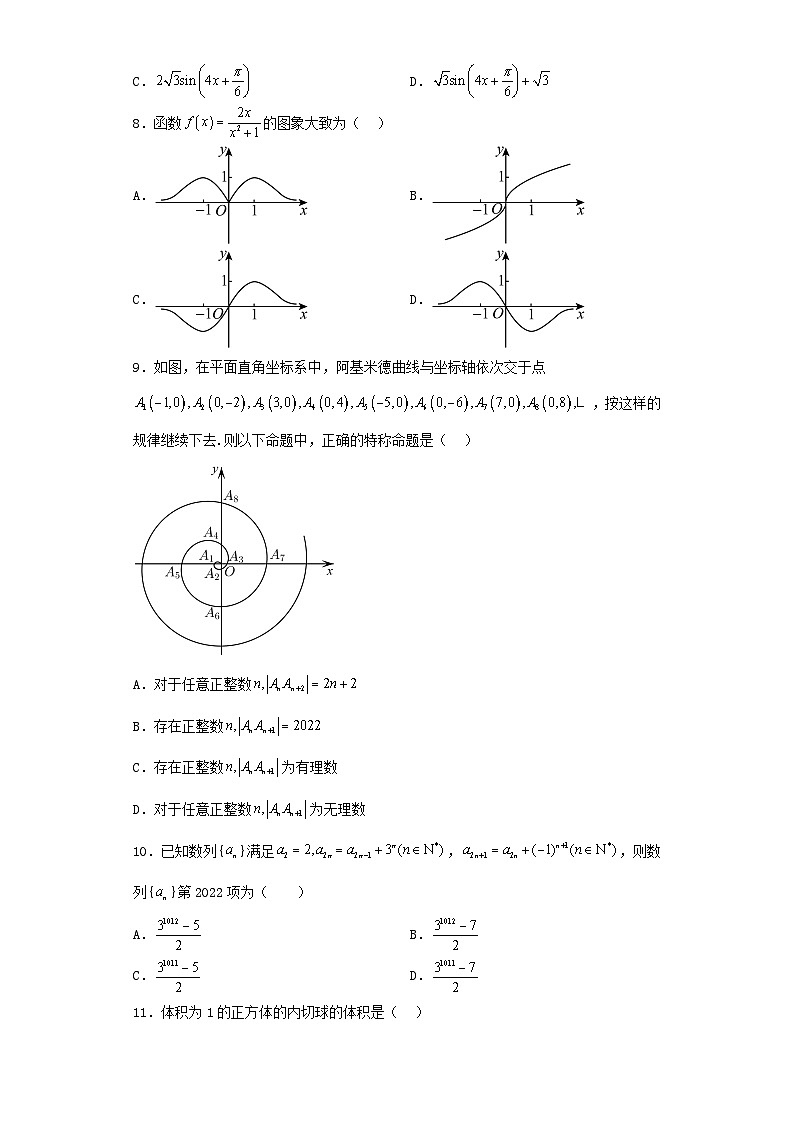
安徽省2022-2023学年高三下学期第三次模拟考试文科数学试卷学校:___________姓名：___________班级：__________一、单选题1．设集合，，则（    ）A． B． C． D．2．已知复数z满足z=2+，则复数z的虚部为（    ）A．1 B．-2 C．2 D．-23．“且”是“”的（    ）A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分又不必要条件4．若角的终边经过点，且，则实数的取值范围为（    ）A． B． C． D．5．如图是某届国际数学家大会的会标，现在有4种颜色给其中5个小区域涂色，规定每个区域只涂一种颜色，相邻区域颜色不相同，则不同的涂色方案种数为（    ）A．72 B．48 C．36 D．246．正四面体ABCD中，E，F分别是AB和CD的中点，则异面直线CE和AF所成角的余弦值为（    ）A． B． C． D．7．已知函数的最小正周期为，最大值为，则函数的解析式为（    ）A． B．C． D．8．函数的图象大致为（    ）A． B．C． D．9．如图，在平面直角坐标系中，阿基米德曲线与坐标轴依次交于点，按这样的规律继续下去.则以下命题中，正确的特称命题是（    ）A．对于任意正整数B．存在正整数C．存在正整数为有理数D．对于任意正整数为无理数10．已知数列{}满足，，则数列{}第2022项为（　　）A． B．C． D．11．体积为1的正方体的内切球的体积是（    ）A． B． C． D．12．已知某地区中小学生人数如图①所示，为了解该地区中小学生的近视情况，卫生部门根据当地中小学生人数，用分层抽样的方法抽取了10%的学生进行调查，调查数据如图②所示，则估计该地区中小学生的平均近视率为（    ）A．50% B．32% C．30% D．27% 二、填空题13．骑自行车是一种环保又健康的运动，如图是某一自行车的平面结构示意图，已知图中的圆（前轮），圆（后轮）的半径均为，，，均是边长为的等边三角形.设点为后轮上的一点，则在骑行该自行车的过程中，的最大值为______.14．若直线与圆交于，两点，且，关于直线对称，动点在不等式组表示的平面区域内部及边界上运动，的取值范围是______ ．15．已知满足，当，若函数在上恰有八个不同的零点，则实数的取值范围为__________.16．若直线与函数的图象相切，则__________. 三、解答题17．已知的内角A，B，C的对边分别为a，b，c，且.(1)求角B；(2)若b=4，求周长的最大值.18．2022年2月20日，北京冬奥会在鸟巢落下帷幕，中国队创历史最佳战绩．北京冬奥会的成功举办推动了我国冰雪运动的普及，让越来越多的青少年爱上了冰雪运动．某校体育组组织了一次冰雪运动趣味知识竞赛，100名喜爱冰雪运动的学生参赛，现将成绩制成如下频率分布表．学校计划对成绩前15名的参赛学生进行奖励，奖品为冬奥吉祥物冰墩墩玩偶．成绩分组频率0.080.260.420.180.06 (1)试求众数及受奖励的分数线的估计值；(2)从受奖励的15名学生中按表中成绩分组利用分层抽样抽取5人．现从这5人中抽取2人，试求这2人成绩恰有一个不低于90分的概率．19．如图，在三棱锥中，，为的中点，. (1)证明：平面平面；(2)若是边长为的等边三角形，点在棱上，，且二面角的大小为，求三棱锥的体积.20．已知圆，圆，，当两个圆有公共点时，所有可能的公共点组成的曲线记为.（1）求出曲线的方程；（2）已知向量，，，为曲线上不同三点，，求面积的最大值.21．已知函数．(1)讨论在上的单调性；(2)若，证明：函数在上有且仅有三个零点．22．设函数，.(1)求函数的单调递增区间；(2)求函数在区间上的值域.23．已知．(1)解不等式；(2)若关于x的不等式在R上恒成立，求实数m的取值范围．
参考答案：1．C【分析】解集合A中的不等式，求集合B中函数的值域，得到两个集合，再求交集.【详解】由，解得，又，函数单调递增，则，，得故选：C2．D【分析】根据复数的乘、除法运算可得，结合复数虚部的定义即可得出结果.【详解】由，得，所以复数z的的虚部为-2.故选：D.3．B【分析】根据充分、必要条件结合不等式性质理解判断.【详解】若且，例如满足条件，但不满足若，则，且∴“且”是“”的必要不充分条件故选：B.4．D【分析】把点坐标中角度化为锐角，根据三角函数定义取锐角并利用两角和的正切公式化简计算．【详解】，，，，，，，，，..故选：D.5．A【分析】分两种涂色方法：涂4种颜色和3种颜色，首先确定可涂相同颜色的区域，再应用分类分步计数求不同的涂色方案数.【详解】由图知：两组颜色可以相同，若涂4种颜色：颜色相同，则4种选一种涂有，余下3种颜色涂3个区域有，共种，同理颜色相同也有24种；若涂3种颜色，则、分别涂相同的颜色，首先4种颜色选3种有种，再所选3种中选一种涂5有种，余下2种颜色涂、个区域有，共有种；综上，共有72种.故选：A6．C【分析】连接，取的中点，连接，则可得∥，所以可得异面有线CE和AF所成角，然后利用余弦定理求解即可【详解】连接，取的中点，连接，因为为的中点，所以∥，所以为异面有线CE和AF所成角或其补角，设正四面体的棱长为2，则，,所以，所以在中，由余弦定理得,所以异面有线CE和AF所成角的余弦值为，故选：C7．B【分析】利用辅助角公式将解析式化简成，再根据周期求得，利用最大值求得，即可得到答案；【详解】，因为，即，所以，因为最大值为，所以，则，则．故选：B.8．C【分析】利用排除法及奇函数的性质，结合基本不等式即可求解.【详解】由，解得，所以函数的定义域为，所以，所以为奇函数，排除A ；当时，，排除D ；当时，，所以，（当且仅当时等号成立）即，排除B；所以C正确.故选：C.9．C【分析】由选项的命题为全称命题，排除；又，从而即可求解.【详解】解：选项的命题为全称命题，故排除；由，可知为奇数，因为2022为偶数，故排除选项；当，易知，故正确选项为.故选：C.10．A【分析】先通过条件得到，再利用累加法即可求解.【详解】解：由.得，又，可得所以，，，……，，将上式相加得，故选：A.11．A【分析】如图可知球的半径为，结合球的体积公式即可求解．【详解】如图，因为正方体的体积为1，所以其边长为1其内切球的球心为正方体的中心，半径为 则球的体积为．故选：A 12．D【分析】先利用扇形统计图求出抽取的样本容量及小学生、初中生、高中生的人数，再利用条形统计图求出样本容量中近视的学生人数，从而求出平均近视率，得出结果.【详解】根据题意，抽取的样本容量为，其中小学生、初中生、高中生抽取人数分别为：350，450，200，根据图②知抽取的小学生、初中生、高中生中，近视的人数分别为：35，135，100，所以该地区学生的平均近视率为，故选：D.13．【分析】方法一：以为坐标原点建立平面直角坐标系，设，根据向量数量积的坐标运算和三角恒等变换知识可表示出，则当时可得所求最大值；方法二：根据向量线性运算可得，利用向量数量积的定义和运算律可化简得到，由此可求得最大值.【详解】方法一：以点为坐标原点，为轴负半轴建立如图所示的平面直角坐标系，则，，点在以为圆心，为半径的圆上，可设，，，，则当时，取得最大值.方法二：，则当与同向，即时，取得最大值为.14．【分析】首先根据关于直线对称，求出与的值，再集合不等式组画出可行域，根据斜率的几何含义即可求解.【详解】解：由题意，得直线垂直于直线 ，即直线为 又圆心在直线上， 因此，题中不等式组为，作出不等式组表示的平面区域，如图所示设，为区域内的动点，可得表示直线的斜率运动点，可得当与原点重合时，为斜率在正数范围内的最小值；当与重合时，为斜率在负数范围内的最大值或，得的取值范围是.故答案为：15．【分析】由已知条件得出函数的周期，由可得或，由题意作出函数在上的大致图象，数形结合得答案．【详解】因为，所以为周期是8的周期函数，则，由，得或，作出函数在上的大致图象，如图，由图可知，在上，函数的图象与直线有六个交点，即时，有六个实根，从而时，应该有两个实根，即函数的图象与直线有两个交点，故，得.故答案为：.16．1【分析】利用导数的几何意义即可求得答案.【详解】由题意，可得，因为直线与函数的图象相切，故设切点为，则，故，则，故，故答案为：117．(1)；(2)12. 【分析】（1）利用差角的余弦公式，结合正弦定理，化简计算作答.（2）利用余弦定理，结合均值不等式求出a+c的最大值【详解】（1）因为，则，在中，由正弦定理得，，而，即，整理得，即，又，解得，所以.（2）在中，由余弦定理得：，即，而，于是得，当且仅当a=c=4时取“=”，因此，当a=c=4时，a+c取最大值8，从而a+b+c取最大值12，所以周长的最大值为12.18．(1)众数为75，估计值为(2) 【分析】（1）根据表格提供数据求得众数，结合百分位数的求法求得受奖励的分数线的估计值.（2）利用列举法，结合古典概型的概率计算公式计算出所求的概率.(1)众数为75，竞赛成绩在分的人数为，竞赛成绩在的人数为，故受奖励分数线在之间，设受奖励分数线为，则，解得，故受奖励分数线的估计值为．(2)由（1）知，受奖励的15人中，分数在的人数为9，分数在的人数为6，利用分层抽样，可知分数在的抽取3人，分数在的抽取2人，设分数在的2人分别为，分数在的3人分别为，所有的可能情况有，，，，，，，，，，共10种，满足条件的情况有，，，，，共6种 ，故所求的概率为19．(1)证明见解析(2) 【分析】（1）由等腰三角形三线合一性质可得；利用线面垂直判定可证得平面，由面面垂直的判定可得结论；（2）以为坐标原点建立空间直角坐标系，设，利用二面角的向量求法可构造方程求得的值，利用棱锥体积公式可求得结果.【详解】（1），为中点，，又，，平面，平面，平面，平面平面.（2）以为坐标原点，正方向为轴，过作垂直于的直线为轴，可建立如图所示空间直角坐标系，设，则，，，，，设平面的法向量，则，令，解得：，，；轴平面，平面的一个法向量；二面角的大小为，，解得：；，.20．（1）（2）【详解】试题分析：（1）看到具有对称性所以要联想到椭圆或双曲线的定义，曲线上的点满足,∴曲线是以为焦点的椭圆（2）∵，∴三点共线，且直线的斜率为，∴直线的方程为，与椭圆方程联立得，借助弦长公式求得三角形的底边长，利用椭圆得参数方程设出动点设，利用点到直线距离公式求得高的最大值，从而得三角形面积最大值试题解析：（1）曲线上的点满足,∴曲线是以为焦点的椭圆∴∴曲线的方程是                                       （2）∵，∴三点共线，且直线的斜率为，∴直线的方程为，与椭圆方程联立得，∴ . 设，∴到直线的距离，∴，∴的最大值为.点睛：看到此类题首先联想到圆锥曲线的三个方程定义，根据定义得几何关系从而确定方程求解，在求三角形面积最值问题时首先明确其表达式一般是算弦长，算高，对于本题而言，要特别注重参数方程在此题得应用，这样求解高显得很简单21．(1)单调递增区间是，递减区间是(2)证明见解析 【分析】（1）求得导数，结合导数的符号，即可求得函数的单调区间，得到答案；（2）化简函数，得到是偶函数，转化为确定时，的零点个数即可，分，和，三种情况讨论，结合单调性和最值，即可求解.【详解】（1）解：由函数，可得令，可得，当时，，单调递增；当时，，单调递减，所以的单调递增区间是，递减区间是．（2）解：证明：，因为，所以0是的一个零点．又因为，所以是偶函数，即要确定在上的零点个数，需确定时，的零点个数即可．①当时，，令，即，或，当时，，单调递减，且，当时，，单调递增，且，所以在上有唯一零点．②当时，由于，．，而在单调递增，．所以恒成立，故在无零点，所以在有一个零点．由于是偶函数，所以在有一个零点，而，综上所述，函数在上有且仅有三个零点．22．(1)（）(2) 【分析】（1）令（），解得答案.（2）令，可得，计算最值得到值域.【详解】（1）令（），得（），函数的单调递增区间是（）（2）令，可得，当，即时，，当，即时，.函数的值域为23．(1)(2) 【分析】（1）分别讨论，去掉绝对值，分别求出每个不等式的解集，再求并集即可.（2）由题可得，再利用绝对值三角不等式求出，解不等式即可.【详解】（1）解： ①当时，可化为，解得，无解；②当时，可化为，解得，故；③当时，可化为，解得，故．综上所示，不等式的解集为；（2）关于x的不等式在R上恒成立，即，∵，当且仅当，即时等号成立，∴，∴，解得，故实数m的取值范围为．