广西邕衡金卷2023届高三第三次适应性考试数学（理）试题（含解析）

广西邕衡金卷2023届高三第三次适应性考试数学（理）试题

学校:___________姓名：___________班级：___________考号：___________

一、单选题

1．已知，，则（    ）

A． B． C． D．

2．已知复数（，i为虚数单位），且，则z在复平面内对应点所在象限为（    ）

A．第一象限 B．第二象限 C．第三象限 D．第四象限

3．已知X的分布列为

且Y＝aX+3，E（Y），则a为（    ）

A．1 B．2 C．3 D．4

4．荀子《劝学》中说：“不积跬步，无以至千里；不积小流，无以成江海．”所以说学习是日积月累的过程，每天进步一点点，前进不止一小点．我们可以把看作是每天的“进步”率都是1%，一年后是；而把看作是每天“退步”率都是1%，一年后是；这样，一年后的“进步值”是“退步值”的倍．那么当“进步”的值是“退步”的值的2倍，大约经过（    ）天．（参考数据：，，）

A．9 B．15 C．25 D．35

5．抛物线的焦点为F，点，P为抛物线上的动点，则的最小值为（    ）

A． B．3 C．2 D．

6．已知和是两个正交单位向量，，且，则（    ）

A．2或3 B．2或4 C．3或5 D．3或4

7．在中，若，，则（    ）

A． B． C． D．

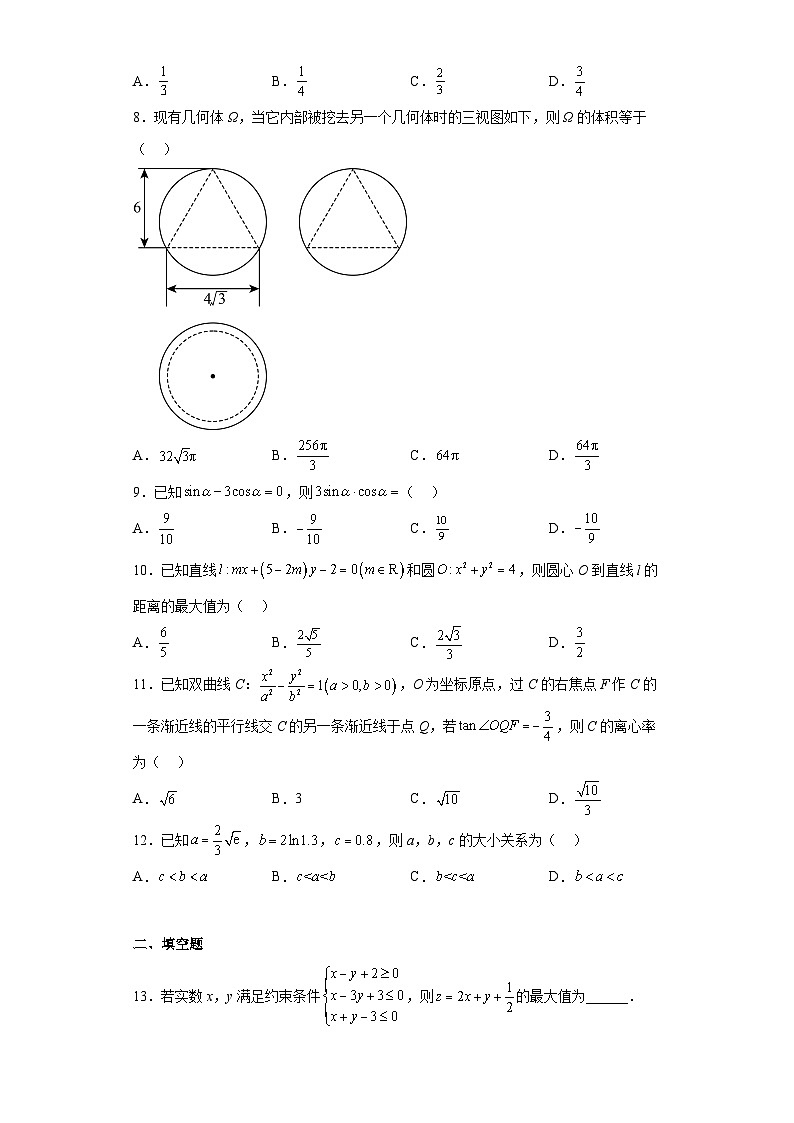
8．现有几何体Ω，当它内部被挖去另一个几何体时的三视图如下，则Ω的体积等于（    ）

A． B． C． D．

9．已知，则（    ）

A． B． C． D．

10．已知直线和圆，则圆心O到直线l的距离的最大值为（    ）

A． B． C． D．

11．已知双曲线C：，O为坐标原点，过C的右焦点F作C的一条渐近线的平行线交C的另一条渐近线于点Q，若，则C的离心率为（    ）

A． B．3 C． D．

12．已知，，，则a，b，c的大小关系为（    ）

A． B． C． D．

二、填空题

13．若实数x，y满足约束条件，则的最大值为______．

14．若，那么的值为_________．

15．如图，有一半径为单位长度的球内切于圆锥，则当圆锥的侧面积取到最小值时，它的高为______．

16．关于函数有如下四个命题：

①的一个周期是π；

②的对称中心是；

③在上的最小值是；

④在内的所有零点之和为．

其中所有真命题的序号是______．

三、解答题

17．已知数列的首项为2，且满足（且），．

(1)求的通项公式；

(2)设，求的前n项和．

18．为深入学习党的二十大精神，我校团委组织学生开展了“喜迎二十大，奋进新征程”知识竞赛活动，现从参加该活动的学生中随机抽取了100名，统计出他们竞赛成绩分布如下：

(1)求抽取的100名学生竞赛成绩的方差（同一组中数据用该组区间的中点值为代表）；

(2)以频率估计概率，发现我校参赛学生竞赛成绩X近似地服从正态分布，其中近似为样本平均分，近似为样本方差，若，参赛学生可获得“参赛纪念证书？”；若，参赛学生可获得“参赛先锋证书”.

①若我校有3000名学生参加本次竞赛活动，试估计获得“参赛纪念证书”的学生人数（结果保留整数）；

②试判断竞赛成绩为96分的学生能否获得“参赛先锋证书”.

附：若，则，，；抽取的这100名学生竞赛成绩的平均分.

19．如图，在多面体ABCDE中，平面平面ABC，平面ABC，和均为正三角形，，点M为线段CD上一点．

(1)求证：；

(2)若EM与平面ACD所成角为，求平面AMB与平面ACD所成锐二面角的余弦值．

20．已知抛物线：，圆：，点F为抛物线的焦点，点A为抛物线上的一点，，且点A的纵坐标为．

(1)求抛物线的方程；

(2)点P（不是原点）是上的一点，过点P作的两条切线分别交于M，N两点（异于点P），E为线段MN中点．若，求点P的坐标．

21．已知函数．

(1)若，求在处的切线方程；

(2)若有两个不同零点，证明：．

22．在平面直角坐标系中，曲线C的参数方程为（t为参数，且），曲线C与x轴交于A点，与y轴交于B点．

(1)求；

(2)以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求以线段AB为直径的圆M的极坐标方程．

23．已知a，b均为正实数，且，证明：

(1)；

(2)．

参考答案：

1．B

【分析】根据指数函数的图象与性质，求得集合，结合集合并集的运算，即可求解.

【详解】由题意，集合，

又因为，可得．

故选：B．

2．D

【分析】根据复数的乘法计算和复数的相等即可求解.

【详解】，

所以，

由复数相等得，

在复平面对应点坐标在第四象限，

故选：D．

3．B

【分析】利用期望的计算公式，计算出EX，再由期望的性质，Y＝aX+3，求出a即可．

【详解】先求出（﹣1）01．

再由Y＝aX+3得．

∴a（）+3，解得a＝2．

故选：B．

【点睛】本题主要考查离散型随机变量的期望及期望的性质，考查了基本运算的能力，属于基础题．

4．D

【分析】设经过x天“进步”的值是“退步”的值的2倍，则，然后利用对数的运算和题目所给的数据求出的值即可.

【详解】设经过x天“进步”的值是“退步”的值的2倍，则，

∴，

故选：D．

5．A

【分析】利用抛物线定义，结合图形可解.

【详解】如图，过点P作PH垂直于准线，垂直为H，

根据抛物线的定义，所以当A，P，H三点共线时最小，

此时.

故选：A．

6．B

【分析】根据题意得到，，求得，集合向量模的计算公式，列出方程，即可求解.

【详解】因为和是正交单位向量，，，

可得，所以，解得或.

故选：B．

7．C

【分析】根据题意，结合正弦定理求得，再由余弦定理，即可求解.

【详解】因为，由正弦定理可得，且，

由余弦定理可得：.

故选：C．

8．B

【分析】本题实质上是求圆锥外接球的体积，根据公式得球的半径R，再根据球的体积公式可得.

【详解】由题意可知，该几何体是球体被挖去一个圆锥，圆锥底面半径为，高为6，

设球的半径为R，可得，解得R=4，

所以体积为．

故选：B

9．A

【分析】先求，再将目标式化为齐次式求解即可.

【详解】由已知得：，所以.

故选：A

10．B

【分析】把直线方程化为，求得直线过定点，结合圆的几何性质，即可求解.

【详解】由题意，直线可化为，

联立方程组，解得，即直线过定点，

又由，可得定点在圆内，

由圆的几何性质知，圆心到直线的距离．

故选：B.

11．D

【分析】结合图形可得，利用诱导公式和二倍角公式求得，然后由公式可得.

【详解】设渐近线的倾斜角为，则，

，则，

解得（舍去）或，

∴，∴.

故选：D．

12．C

【分析】由指数幂的运算性质得到，得到，构造函数，利用导数取得函数得到单调性，得到，得到，结合，得到，即可求解.

【详解】由指数幂的运算公式，可得，所以，

构造函数，其中，则，

当时，；当时，，

所以函数在上单调递增，在上单调递减，

故，故，当且仅当时取等号，

由于，则，则，所以，所以，所以.

故选：C.

13．5

【分析】先作可行域，再作直线，平移直线确定最优解，然后可得.

【详解】根据题意作可行域如图，

作直线，由图可知，平移直线到l位置，即过点A时，取得最大值.

解方程组得，

代入，得.

故答案为：5

14．

【分析】根据题意利用赋值法分析运算.

【详解】令，可得；

令，可得；

所以．

故答案为：.

15．/

【分析】由，求得，得到侧面积，令，得到，求得函数的单调性，进而得到答案.

【详解】如图所示，设，半径，高，

球半径为单位长度，

因为，可得，即，

所以，解得，

所以侧面积，

令，可得，

令，可得，解得．

当，，单调递减；

当，，单调递减，

所以时侧面积有最小值．

故答案为：.

16．②④

【分析】根据函数的周期性和对称性公式以及导数确定单调性结合特殊点函数值即可求解.

【详解】对①，，故①错误；

对②，因为，

所以关于点对称，故②正确；

对③，，

令，

则，

当，；，，

所以在上的最小值是；

又，

而，

所以，故③错误；

对④，得或，

因为，

所以当时，解得，

当时，

因为在上函数的对称轴为，

所以它的两零点之和为，

故在内的所有零点之和为，故④正确．

故答案为：②④.

17．(1)

(2)

【分析】（1）因式分解可知为等比数列，然后可解；

（2）利用对数运算裂项可解.

【详解】（1）由得，

因为，所以，所以，即，

又，所以是以2为首项和公比的等比数列，所以．

（2）由得，

18．(1)

(2)①2456②能获得“参赛先峰证书”

【分析】（1）利用公式直接求出方差即可；

（2）①结合给的概率和正态分布的性质，确定获得“参赛纪念证书”，进而计算可得人数；

②利用正态分布的知识求出，即，进而可得结果.

【详解】（1）由题意，抽取的这100名学生竞赛成绩的平均分，

所以100名学生本次竞赛成绩方差

；

（2）①由于近似为样本成绩平均分，近似为样本成绩方差，

所以，可知，，

由于竞赛成绩X近似地服从正态分布，

因此竞赛学生可获得“参赛纪念证书”的概率

，

所以，

故估计获得“参赛纪念证书”的学生人数为2456，

②当时，即时，参赛学生可获得“参赛先锋证书”，

所以竞赛成绩为96分的学生能获得“参赛先峰证书”.

19．(1)证明见解析；

(2).

【分析】（1）取AC中点O，利用面面垂直的性质、线面垂直的性质证明即可推理作答.

（2）利用（1）中信息，建立空间直角坐标系，借助空间向量求解作答.

【详解】（1）取AC中点O，连接DO、OB，在正和正中，，

则，而平面平面ABC，

平面平面，平面ACD，平面ABC，于是平面ABC，平面ACD，

又平面ABC，即有，而．因此四边形DOBE是平行四边形，则，

从而平面ABC，平面ADC，

所以.

（2）由（1）知，平面ADC，为EM与平面ADC的所成角，即，

在中，，即M为DC中点，

由（1）知，两两垂直，建立如图所示的空间直角坐标系，

则，，

显然平面DAC的一个法向量为，设平面MAB的一个法向量为，

则，令，得，

，

所以平面AMB与平面ACD所成锐二面角的余弦值为．

20．(1)

(2)

【分析】（1）根据抛物线的焦半径公式可解；

（2）设，，，切线方程为，由圆心到直线的距离等于半径得关于k的方程，根据韦达定理可得的值，再联立切线方程和抛物线方程可得与的关系，然后根据可解.

【详解】（1）由题意可得，解得，

所以抛物线的方程为．

（2）设，，，由题知，，，且切线的斜率存在．

设过点的圆的切线方程为，即．

圆心到切线的距离为1，得到，

整理得，

设PM，PN的斜率分别为，，则有，，

联立，得，

因为点P是直线与抛物线的一个交点，有，

同理可得，

因为E为MN中点，则有，又，所以点在PE，从而有，

，

，所以，解得，

所以点P的坐标为.

【点睛】本题难点有二，一是MN的斜率如何转化为点P坐标来表示，可通过联立切线方程和抛物线方程，利用韦达定理得与的关系进行转化；二是如何表示PE的斜率，主要考察学生的观察能力，根据垂直平分线的性质即可得到.

21．(1)

(2)证明见解析

【分析】（1）求出切线斜率，根据点斜式可得.

（2）由得，故考虑构造函数，先证，利用的单调性去证明即可.

【详解】（1）当时，，            

故，，

故在处的切线方程为，即.

（2）证明：不妨设，设，则，         

当时，，当时，，

所以在单调递减，在单调递增，                        

可知，也是的两个零点，且，，于是，                

设，

因为．       

设，

当时，，

故在单调递增，

所以，从而，

因此在单调递增．                 

又，故，故，于是．              

又在单调递减，故                            

即，故

【点睛】关键点点睛：第一个关键点是从结论分析，由得，故构造函数；第二个关键点是能利用函数的最值得到，进而证明.

22．(1)

(2)

【分析】（1）分别令和，求得的坐标，进而求得的长；

（2）由（1）求得圆M的直角坐标方程为，结合极坐标与直角的互化公式，即可求解.

【详解】（1）解：令，则，解得或（舍去），

则，即．

令，则，解得或（舍去），

则，即，

所以.

（2）解：由（1）可知的中点为，则以线段为直径的圆M的半径为，

所以圆M的直角坐标方程为，即，

由，可得，直线的极坐标方程为．

23．(1)证明见解析

(2)证明见解析

【分析】（1）由柯西不等式有，结合题意，即可求解；

（2）根据题意得到，结合，结合基本不等式，即可求解．

【详解】（1）证明：由柯西不等式有，

又因为，则，当且仅当时，取等号，

所以．

（2）证明：因为，所以，

所以，所以，

当且仅当，即时取等号，．