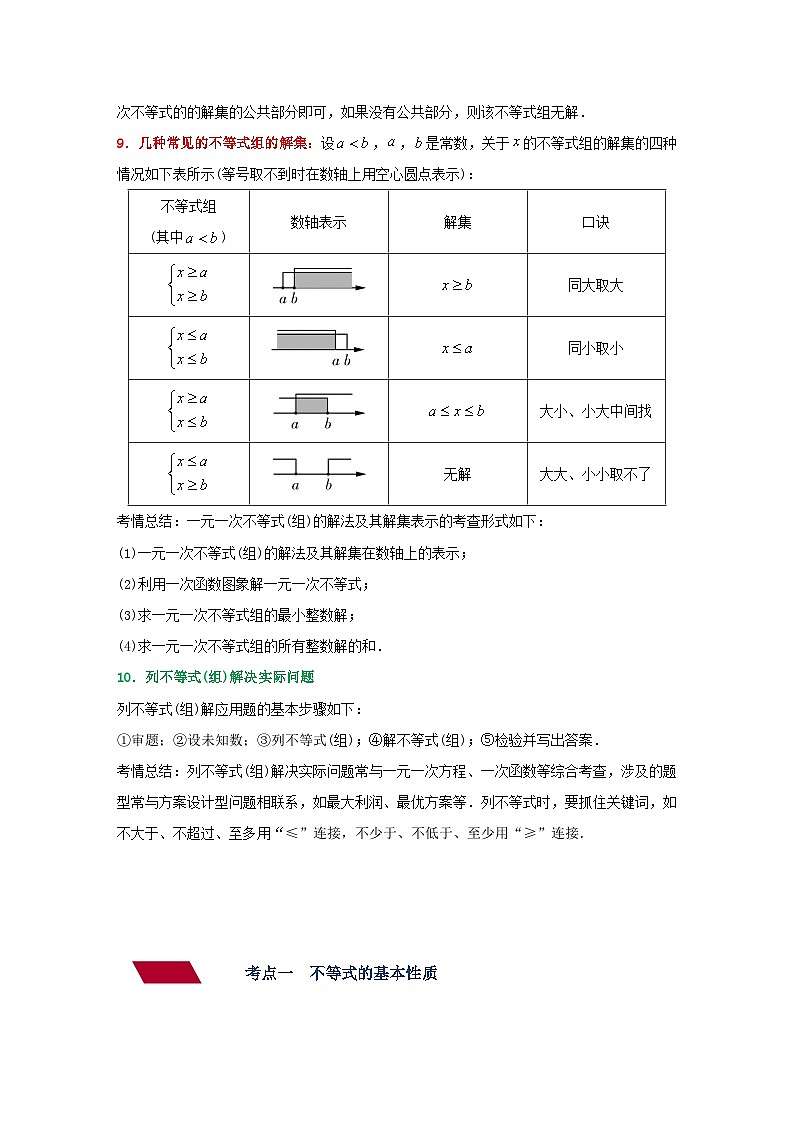
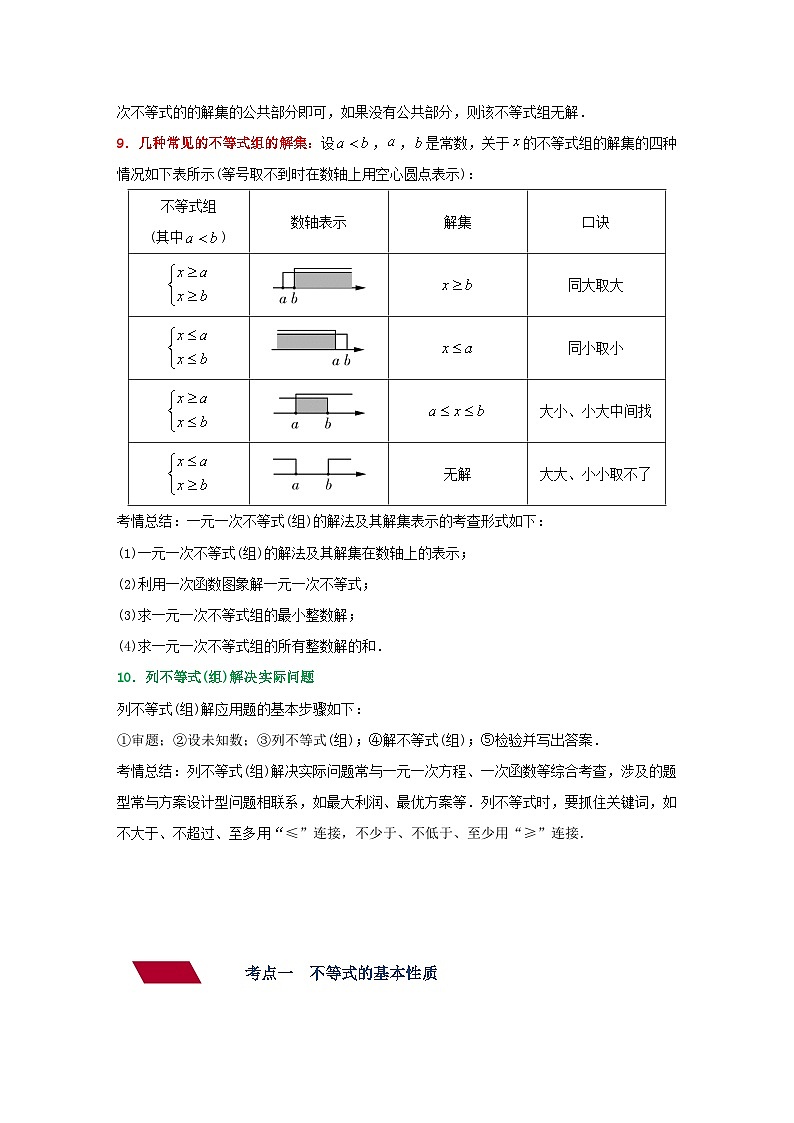
第7讲 一元一次不等式（组）（讲义）（教师版含解析）中考数学一轮复习讲义+训练

中考数学一轮复习专题讲义+强化训练(全国通用)

第五讲  一元二次方程

一、13个必备知识点

考点一  等式的性质

考点二  解一次方程(组)

考点三  含参数的一次方程(组)

考点四  一元一次方程的应用

考点五  二元一次方程组的应用

一、13个必备知识点

1．一元二次方程：只含有一个未知数，并且未知数的最高次数是2的整式方程叫做一元二次方程．

2．一般形式：(其中为常数，)，其中分别叫做二次项、一次项和常数项，分别称为二次项系数和一次项系数．

注意：(1)在一元二次方程的一般形式中要注意，因为当时，不含有二次项，即不是一元二次方程；(2)一元二次方程必须具备三个条件：①必须是整式方程；②必须只含有一个未知数；③所含未知数的最高次数是2．

3．直接开平方法：适合于或形式的方程．

4．配方法：(1)化二次项系数为1；(2)移项，使方程左边只含有二次项和一次项，右边为常数项；

(3)方程两边同时加上一次项系数一半的平方；(4)把方程整理成的形式；

(5)运用直接开平方法解方程．

5．公式法：(1)把方程化为一般形式，即；(2)确定的值；(3)求出的值；(4)将的值代入即可．

6．因式分解法：基本思想是把方程化成的形式，可得或．

7．根的判别式：一元二次方程是否有实数根，由的符号来确定，我们把叫做一元二次方程根的判别式．

8．一元二次方程根的情况与判别式的关系

(1)当时，方程有两个不相等的实数根；

(2)当时，方程有1个(两个相等的)实数根；

(3)当时，方程没有实数根．

9．根与系数关系：对于一元二次方程(其中为常数，)，设其两根分别为，，则，．

列一元二次方程解应用题步骤和列一元一次方程(组)解应用题步骤一样，即审、设、列、解、验、答六步．列一元二次方程解应用题，经济类和面积类问题是常考内容．

10．增长率等量关系

(1)增长率=增长量÷基础量．(2)设为原来量，为平均增长率，为增长次数，为增长后的量，则；当为平均下降率时，则有．

11．利润等量关系：(1)利润=售价－成本．(2)利润率=×100％．

12．面积问题

(1)类型1：如图1所示的矩形长为，宽为，空白“回形”道路的宽为，则阴影部分的面积为．

(2)类型2：如图2所示的矩形长为，宽为，阴影道路的宽为，则空白部分的面积为．

(3)类型3：如图3所示的矩形长为，宽为，阴影道路的宽为，则4块空白部分的面积之和可转化为．

图1                      图2                          图3

13. 碰面问题(循环问题)

(1)重叠类型(双循环)：n支球队互相之间都要打一场比赛，总共比赛场次为m。

∵1支球队要和剩下的(n－1)支球队比赛，∴1支球队需要比(n－1)场

∵存在n支这样的球队，∴比赛场次为：n(n－1)场

∵A与B比赛和B与A比赛是同一场比赛，∴上述求法有重叠部分.

∴m=

(2)不重叠类型(单循环)：n支球队，每支球队要在主场与所有球队各打一场，总共比赛场次为m。

∵1支球队要和剩下的(n－1)支球队比赛，∴1支球队需要比(n－1)场

∵存在n支这样的球队，∴比赛场次为：n(n－1)场.

∵A与B比赛在A的主场，B与A比赛在B的主场，不是同一场比赛，∴上述求法无重叠.

∴m=

考点一  一元二次方程的解

1．已知方程3x2﹣(k﹣1)x﹣k+7＝0的一个根为0，则k的值为(　　)

A．3 B．﹣3 C．7 D．﹣7

2．关于x的一元二次方程ax2+bx+c＝0(a≠0)中，它的一个根为﹣1，则(　　)

A．a+b+c＝0 B．a+b﹣c＝0 C．a﹣b+c＝0 D．a﹣b﹣c＝0

3．若x＝3是关于x的方程﹣3a＝0的一个根，则在平面直角坐标系中，一次函数y＝ax+2的图象不经过(　　)

A．第一象限 B．第二象限 C．第三象限 D．第四象限

考点二  解一元二次方程

1．用适当的方法解一元二次方程

(1)x2﹣9＝0        (2)2x2﹣7x＝0            (3)x2﹣2x﹣5＝0  

(4)3x2﹣1＝4x      (5)3(x﹣2)2＝x(x﹣2) (6)(x+8)(x+1)＝﹣12．

2．选用适当方法解一元二次方程

(1)(x﹣2)2＝(2x+5)2     (2)(x2+3x)2﹣2(x2+3x)﹣8＝0

（3）x2﹣2mx+m2﹣n2＝0      (4)(m﹣1)x2+(m﹣2)x﹣1＝0．

3．解下列一元二次方程

(1)4x2﹣16x+15＝0(用配方法解)

(2)9﹣x2＝2x2﹣6x(用分解因式法解)

(3)(x+1)(2﹣x)＝1(选择适当的方法解)

考点三  配方法求最值

1．已知x，y为实数，求代数式x2+y2+2x﹣4y+7的最小值　 　．

2．关于x的式子x2+6x﹣9，当x＝　   　时，式子有最　   　值，且这个值为　   　．

3．已知实数m，n满足m﹣n2＝1，则代数式m2+2n2+4m﹣1的最小值等于？

4．当a，b为何值时，多项式a2+b2﹣4a+6b+18有最小值？并求出这个最小值．

5．阅读下列材料：

我们把多项式a2+2ab+b2及a2﹣2ab+b2叫做完全平方式，如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法．配方法是一种重要的解决数学问题的方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决一些与非负数有关的问题或求代数式的最大值、最小值等．

例如：x2+2x﹣3＝(x2+2x+1)﹣4＝(x+1)2﹣22＝(x+1+2)(x+1﹣2)＝(x+3)(x﹣1)；

x2﹣10x+30＝x2﹣10x+25+5＝(x2﹣10x+25)+5＝(x﹣5)2+5，因为(x﹣5)2≥0，即(x﹣5)2的最小值是0，所以x2﹣10x+30的最小值是5．

根据阅读材料用配方法解决下列问题：

(1)分解因式：x2﹣4x﹣5；

(2)求a2+2a+2021的最小值；

(3)求﹣x2+2x+2019的最大值．

考点四  根的判别式与韦达定理

1．已知关于x的一元二次方程mx2﹣4x+2＝0有两个实数根，则m的取值范围是(　　)

A．m≤2 B．m＜2且m≠0 C．m≠0 D．m≤2且m≠0

2．小刚在解关于x的方程ax2+bx+c＝0(a≠0)时，只抄对了a＝1，c＝4，解出其中一个根是x＝﹣1．他核对时发现所抄的b是原方程中b的相反数．则原方程的根的情况是(　　)

A．有两个不相等的实数根 B．有两个相等的实数根 

C．有一个根是x＝﹣1 D．不存在实数根

3．关于x的方程(x﹣1)(x+2)＝p2(p为常数)的根的情况，下列结论中正确的是(　　)

A．两个正根 B．两个负根 

C．一个正根，一个负根 D．无实数根

4．三角形的两边a、b的夹角为60°且满足方程x2﹣3x+4＝0，则第三边的长是(　　)

A． B．2 C．2 D．3

5．一个等腰三角形的两条边长分别是方程x2﹣9x+18＝0的两根，则该等腰三角形的周长是(　　)

A．12 B．9 C．15 D．12或15

6．关于x的一元二次方程x2﹣4x+m＝0的两实数根分别为x1、x2，且x1+3x2＝5，则m的值为(　　)

A． B． C． D．0

7．设x1，x2是方程x2﹣x﹣2020＝0的两实数根，则x13+2021x2﹣2020＝　     　．

8．已知一元二次方程两个根为a，b，求下列各式的值．

(1)；

(2)．

9．已知关于x的一元二次方程(x﹣m)2+6x＝4m﹣3有实数根．

(1)求m的取值范围；

(2)设方程的两实根分别为x1与x2，若x1x2﹣x12﹣x22＝﹣7，求m的值．

10．如图，在△ABC中，∠C＝90．，∠A，∠B，∠C所对的边分别为a，b，c．将形如ax2+cx+b＝0的一元二次方程称为“直系一元二次方程”．

(1)请直接写出一个“直系一元二次方程”；

(2)求证：关于x的“直系一元二次方程”ax2+cx+b＝0必有实数根；

(3)若x＝﹣1是“直系一元二次方程”ax2+cx+b＝0的一个根，且S△ABC＝3，求的值．

11．材料一：法国数学家弗朗索瓦•韦达于1615年在著作《论方程的识别与订正》中建立了方程根与系数的关系，提出一元二次方程ax2+bx+c＝0(a≠0)的根完全由它的系数决定，当b2﹣4ac≥0时有两根：x1＝，x2＝；

于是，两根之和为x1+x2＝；

两根之积为x1⋅x2＝•＝＝．

由于韦达最早发现代数方程的根与系数之间有这种关系，人们把这个关系称为韦达定理，韦达定理对代数学的推进做出了巨大贡献，它最早系统地引入代数符号，推进了方程论的发展，用字母代替未知数，指出了根与系数之间的关系．利用韦达定理可以快速求出两方程根的关系，韦达定理应用广泛，在初等数学、解析几何、平面几何、方程论中均有体现．而且韦达定理为数学中的一元方程奠定了基础，对一元方程的应用创造和开拓了广泛的发展空间．

材料二：已知一元二次方程ax2﹣bx+c＝0(a≠0)的两个根满足，且a、b、c分别是△ABC的∠A、∠B、∠C的对边，若a＝c，求∠B的度数．

解题过程如下：x1+x2＝﹣，x1⋅x2＝＝1，

∵|x1﹣x2|＝，

∴|x1﹣x2|2＝2．

又∵﹣4，

∴＝3，

∵a＞0，b＞0，

∴＝．

如图，过点B作BH⊥AC于点H．则HC＝AC＝b，∴cosC＝，∴∠C＝30°，∴∠B＝120°．

(1)在上题中，将方程改为ax2﹣bx+c＝0(a≠0)，要得到∠B＝120°，而条件“a＝c”不变，那么对应条件中的|x1﹣x2|的值是多少？请说明理由．

(2)已知一元二次方程ax2﹣bx+c＝0(n≥0，a≠0)的两根满足1﹣(x1﹣x2)2＝2|x1﹣x2|，且a、b、c分别是△ABC的∠A、∠B、∠C的对边，若∠A＝30°，∠B＝45°，求n的值．

考点五  一元二次方程的应用

1．2021年是中国历史上的超级航天年，渝飞航模专卖店看准商机，8月初推出了“天问一号”和“嫦娥五号”两款模型．每个“天问一号”模型的售价是90元，每个“嫦娥五号”模型的售价是100元，该店在8月份售出“天问一号”模型400个，“嫦娥五号”模型200个．该店决定从9月1日起推出“逐梦航天、仰望星空”优惠活动，

9月份，每个“天问一号”模型的售价与8月份相同，销量比8月份增加a%；每个“嫦娥五号”模型的售价在8月份的基础上降价a%，销量比8月份增加a%．

(1)用含有a的代数式填表(不需化简)：

（2）据统计，该店在9月份的销售总额比8月份的销售总额增加a%，求a的值．

2．如图，△ABC中，∠C＝90°，BC＝30cm，AC＝40cm，点P从点C开始沿CA边以4cm/s的速度向点A移动，同时，另一点Q由点C开始以3cm/s的速度沿着CB边向点B移动，求几秒钟后，△PCQ的面积等于△ABC面积的？

3．R0，也叫基本传染数，或者基本再生数，英文为Basicreproductionnumber．更确切的定义是：在没有外力介入，所有人都没有免疫力的情况下，一个感染某种传染病的人，总共会传染给其他多少个人的平均数．例如：有1人感染新型冠状病毒，若R0＝3.50，则经两轮传染后感染新型冠状病毒的人数为：1+1×3.50+1×3.50×3.50≈17(人)．时下人心惶惶的新型冠状病毒的基本传染数据估计为3.30到5.40之间．请解答下列问题：

(1)若现有10人感染新型冠状病毒，则经历两轮传染后，感染新型冠状病毒的人数大约在什么范围内(直接写出结果，结果保留整数)？

(2)最近，新型冠状病毒变异出德尔塔毒株，德尔塔变异病毒的R0值极高．若1人患病，在无任何外力影响下经历两轮传染后共有73人感染．

①求德尔塔变异病毒的R0值；

②国家研制出新冠疫苗后发现，通过接种疫苗可以使得R0值随接种人数比例的增高同步降低．例如，当疫苗全民接种率达到40%时，此时的R0值为：R0(1﹣40%)＝0.6R0．若有1人感染德尔塔变异病毒，要在两轮内将总感染人数控制在7人以内，再加以隔离等措施的干涉，就可控制住疫情，则全民接种率至少应该达到多少？

4．某超市销售一种商品，成本价为50元/千克，规定每千克售价不低于成本价，且不高于85元．经市场调查，该商品每天的销售量y(千克)与售价x(元千克)满足一次函数关系，如图所示：

(1)求y与x之间的函数表达式；

(2)该商场销售这种商品要想每天获得1350元的利润，每件商品的售价应定为多少元？

5．“民族要复兴，乡村必振兴”，巴南区积极践行国家乡村振兴战略，大力发展乡村特色产业，丰盛镇脆桃种植基地连续几年产量获得大丰收，该基地采用现场采摘销售和线上销售两种模式．

(1)今年该基地脆桃产量为51000千克，全部售出，其中线上销量不超过现场采摘销量的2倍．求现场采摘销量至少多少千克？

(2)该基地6月份现场采摘销售均价为15元/千克，销售量为1200千克．线上销售均价为10元/千克，销售量为1800千克．7月份现场采摘销售均价上涨了25%，销售量下降了2a%，线上销售均价上涨了a%，销量与6月份一样，7月份销售总金额比6月份销售总金额减少了a%，求a的值．

6．如图，用一段长为30m的篱笆围成一个一边靠墙的矩形苗圃园，墙长为18m，设这个苗圃园垂直于墙的一边AB的长为xm．

(1)用含有x的式子表示BC，并直接写出x的取值范围；

(2)若苗圃园的面积为72m2，求AB的长．

7．某电商公司推出A、B两种类型的超薄全面屏电视机，已知售出2台A型电视机，3台B型电视机的销售额为35500元：售出1台A型电视机，2台型电视机的销售额为20500元．

(1)求每台A型电视机和B型电视机的售价分别是多少元；

(2)该电商公司在8月实行“满减促销”活动，活动方案为：单台电视机满4000元减500元，满9000元减1500元(每台电视机只能参加一次最高满减活动)结果8月A型电视机的销量是B型电视机的，9月该电商公司加大促销活动力度，每台A型电视机按照8月满减后的售价再降a%，销量比8月增加2a%；每台B型电视机按照8月满减后的售价再降a%，销量比8月销量增加a%，结果9月A和B的销售总额比8月A和B的销售总额多a%，求a的值．