2023年山东省泰安市泰山区中考数学一模试卷

2023年山东省泰安市泰山区中考数学一模试卷

学校:___________姓名：___________班级：___________考号：___________

第I卷（选择题）

一、选择题（本大题共12小题，共48.0分。在每小题列出的选项中，选出符合题目的一项）

1.  下面几何体的左视图是(    )

A.
B.
C.
D.

2.  在实数：，，，中，最小的数是(    )

A.  B.  C.  D.

3.  截至年月日，世界第四大水电站云南昭通溪洛渡水电站累计生产清洁电能突破亿千瓦时，相当于替代标准煤约亿吨，减排二氧化碳约亿吨．亿用科学记数法表示为(    )

A.  B.  C.  D.

4.  下列运算结果等于的是(    )

A.  B.  C.  D.

5.  如图，三角形板的直角顶点落在矩形纸片的一边上，若，则的度数是(    )

A.  B.  C.  D.

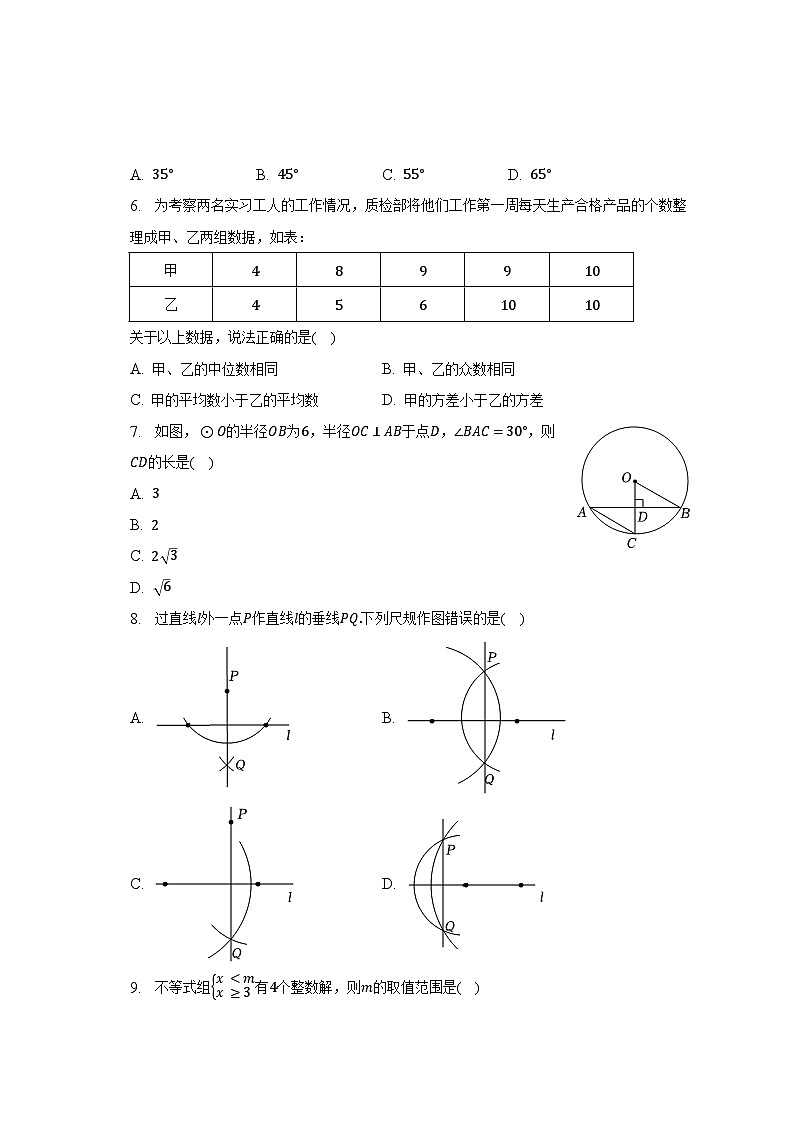
6.  为考察两名实习工人的工作情况，质检部将他们工作第一周每天生产合格产品的个数整理成甲、乙两组数据，如表：

关于以上数据，说法正确的是(    )

A. 甲、乙的中位数相同 B. 甲、乙的众数相同
C. 甲的平均数小于乙的平均数 D. 甲的方差小于乙的方差

7.  如图，的半径为，半径于点，，则的长是(    )

A.
B.
C.
D.

8.  过直线外一点作直线的垂线下列尺规作图错误的是(    )

A.  B.
C.  D.

9.  不等式组有个整数解，则的取值范围是(    )

A.  B.  C.  D.

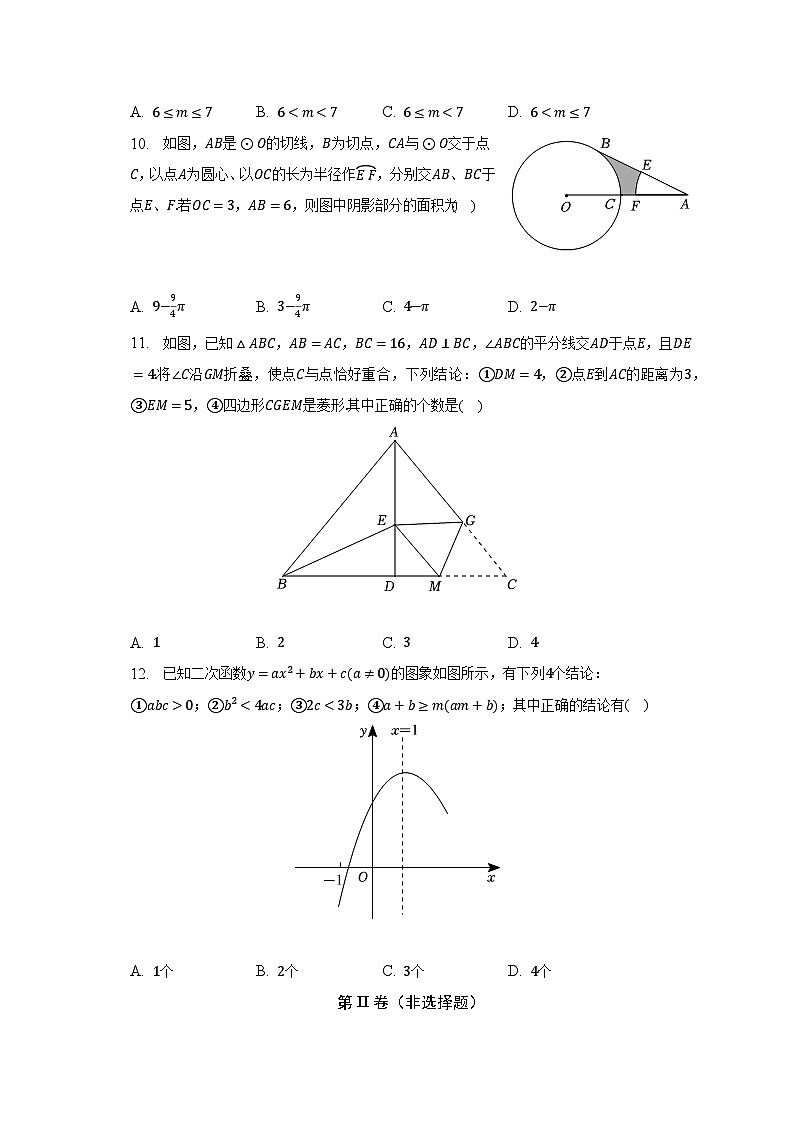
10.  如图，是的切线，为切点，与交于点，以点为圆心、以的长为半径作，分别交、于点、若，，则图中阴影部分的面积为(    )

A.  B.  C.  D.

11.  如图，已知，，，，的平分线交于点，且将沿折叠，使点与点恰好重合，下列结论：，点到的距离为，，四边形是菱形其中正确的个数是(    )

A.  B.  C.  D.

12.  已知二次函数的图象如图所示，有下列个结论：
；；；；其中正确的结论有(    )

A. 个 B. 个 C. 个 D. 个

第II卷（非选择题）

二、填空题（本大题共6小题，共24.0分）

13.  分解因式：______．

14.  不透明布袋中装有除颜色外没有其他区别的个红球和个白球，搅匀后从中摸出一个球，放回搅匀，再摸出一个球，两次都摸出白球的概率是______ ．

15.  我国古代四元玉鉴中记载二果问价问题，其内容如下：九百九十九文钱，甜果苦果买千，甜果九个十一文，苦果七个四文钱，试问甜苦果几个，又问各该几个钱？其意思为：九百九十九文钱买了甜果和苦果共一千个已知十一文钱可买九个甜果，四文钱可买七个苦果，那么甜果、苦果各买了多少个？买甜果和苦果各需要多少文钱？若设买甜果个，买苦果个，根据题意所列方程组是______ ．

16.  数学活动小组到某广场测量标志性建筑的高度如图，他们在地面上点测得最高点的仰角为，再向前至点，又测得最高点的仰角为，点，，在同一直线上，则该建筑物的高度约为______ 精确到参考数据：，，，

17.  根据图中数字的规律，则的值是______．
 

18.  如图，菱形的对角线相交于点，，，点为边上一点，且不与、重合过作于，于，连接，则的最小值等于______ ．

三、解答题（本大题共7小题，共78.0分。解答应写出文字说明，证明过程或演算步骤）

19.  本小题分
先化简，再求值：，其中．
解不等式组：，并把它们的解集在数轴上表示出来．

20.  本小题分
某校为了响应市政府号召，在“创文明城市”活动周中，设置了“：文明礼仪，：环境保护，：卫生保洁，：垃圾分类”四个主题，每个学生选一个主题参与为了解活动开展情况，学校随机抽取了部分学生进行调查，并根据调查结果绘制了如图：条形统计图和扇形统计图．
求本次调查的学生人数和的值；
请补全条形统计图；
学校要求每位同学从星期一至星期五选择两天参加活动如果小明同学随机选择两天，那么其中有一天是星期五的概率是多少？
 

21.  本小题分
如图，反比例函数的图象与正比例函数的图象相交于、两点，点在第三象限，轴．
求反比例函数的表达式；
以、为边作菱形，求点坐标．

22.  本小题分
如图，四边形是的内接四边形，连接，，延长至点．
若，求证：平分；
若，的半径为，求．

23.  本小题分
某中学为落实教育部办公厅关于进一步加强中小学生体质健康管理工作的通知文件要求，决定增设篮球，足球两门选修课程，需要购进一批篮球和足球若购买篮球的数量是足球的倍，购买篮球用了元，购买足球用了元，篮球单价比足球单价贵元．
求篮球和足球的单价分别是多少元；
学校计划采购篮球、足球共个，并要求篮球多于个，且总费用低于元那么有哪几种购买方案？

24.  本小题分
二次函数的图象交轴于点，点两点，交轴于点动点从点出发，以每秒个单位长度的速度沿方向运动，过点作轴交直线于点，交抛物线于点，连接，设运动的时间为秒．
求二次函数的表达式；
连接，当时，求的面积；
在直线上存在一点，当是以为直角的等腰直角三角形时，求此时点的坐标．
 

25.  本小题分
问题：如图，在▱中，，，，的平分线，分别与直线交于点，．
求的长．
探究：
把“问题”中的条件“”去掉，其余条件不变当点与点重合时，求的长．
把“问题”中的条件“，”去掉，其余条件不变，当点，，，相邻两点间的距离相等时，求的值．

答案和解析

1.【答案】 

【解析】解：从左面看，是一个等腰梯形．
故选：．
找到几何体从左面看所得到的图形即可．注意所有的看到的棱都应表现在视图中，看不见的棱用虚线表示．
本题考查了三视图的知识，左视图是从物体的左面看得到的视图．画物体的三视图的口诀为：主、俯：长对正；主、左：高平齐；俯、左：宽相等．
 

2.【答案】 

【解析】解：，，
．
故选：．
由正数都大于，负数都小于，由此即可得到答案．
本题考查实数大小比较，相反数，绝对值，关键是掌握：实数大小的比较方法．
 

3.【答案】 

【解析】解：亿，
故选：．
根据亿，再用科学记数法的表示即可．
本题主要考查科学记数法的知识，熟练掌握科学记数法的形式是解题的关键．
 

4.【答案】 

【解析】解：、，无法计算，故此选项错误；
B、，故此选项错误；
C、，故此选项错误；
D、，故此选项正确．
故选：．
分别利用合并同类项法则以及幂的乘方运算法则、同底数幂的乘除法运算法则化简判断即可．
此题主要考查了合并同类项以及幂的乘方运算、同底数幂的乘除法运算，正确掌握运算法则是解题关键．
 

5.【答案】 

【解析】解：如图，

由题意得：，，
，
．
故选：．
由题意可得，，由平行线的性质可求得，再由补角的定义即可求．
此题考查了平行线的性质，补角，熟记两直线平行，同位角相等是解此题的关键．
 

6.【答案】 

【解析】解：、甲的中位数为，乙的中位数为，故本选项不符合题意；
B、甲的众数为，乙的众数为，故本选项不符合题意；
C、甲的平均数为，乙的平均数为，故本选项不符合题意；
D、甲的方差为，
乙的方差为，
甲的方差小于乙的方差，故本选项符合题意；
故选：．
根据中位数的定义求出甲、乙两组数据的中位数，可以对作出判断；
根据众数是一组数据中出现次数最多的数，据此判断的正误；
利用平均数的计算公式求出甲、乙两组数据的平均数，判断的正误；
分别求出甲、乙两组数据的方差，通过比较方差的大小判断的正误．
此题主要考查了众数、中位数、方差和平均数，关键是掌握三种数的概念和方差公式．
 

7.【答案】 

【解析】解：半径，
，
，
，
，
在中，，
，
，
故选：．
根据垂直定义可得，再利用圆周角定理可得，然后利用直角三角形的两个锐角互余可得，从而在中，利用含度角的直角三角形的性质可求出的长，最后利用线段的和差关系进行计算，即可解答．
本题考查了圆周角定理，含度角的直角三角形，熟练掌握圆周角定理，以及含度角的直角三角形的性质是解题的关键．
 

8.【答案】 

【解析】解：选项A，连接，，，，

，
点在线段的垂直平分线上，
，
点在线段的垂直平分线上，
，故此选项不符合题意；
选项B，连接，，，，

，
点在线段的垂直平分线上，
，
点在线段的垂直平分线上，
，故此选项不符合题意；
选项C，无法证明，故此选项符合题意；
选项D，连接，，，，

，
点在线段的垂直平分线上，
，
点在线段的垂直平分线上，
，故此选项不符合题意；
故选：．
根据作图痕迹结合线段垂直平分线的判定进行分析判断．
本题考查尺规作图，准确识图，掌握线段垂直平分线的判定定理是解题关键．
 

9.【答案】 

【解析】解：关于的不等式组有解，其解集为，
关于的不等式组恰有个整数解，
，
故选：．
根据关于的不等式组的解集和整数解的个数确定关于的不等式组，再求出解集即可．
本题考查一元一次不等式组的整数解，掌握一元一次不等式组的解法，理解一元一次不等式组的整数解的意义是正确解答的前提．
 

10.【答案】 

【解析】解：连接，

是的切线，为切点，
，
，
由题意得：
，
阴影部分的面积的面积扇形的面积扇形的面积


，
故选：．
连接，根据切线的性质可得，从而可得，根据题意可得，然后利用阴影部分的面积的面积扇形的面积扇形的面积，进行计算即可答．
本题考查了切线的性质，扇形面积的计算，熟练掌握切线的性质，以及扇形面积的计算是解题的关键．
 

11.【答案】 

【解析】解：在中，，，，
，
如图，过点作于点，于点，
，，
平分，
，
是的角平分线，
，，
，
，故错误；
由折叠性质可得：，，
设，则，
中，，
，
解得：，
，故正确；
，故错误；
连接，由内心可知平分，
，
由折叠可知，
，
，
，
，
，
，
，
四边形是菱形；故正确，
故选：．
根据等腰三角形的性质得到，如图，过点作于点，于点，根据角平分线的性质得到，，求得，故错误；由折叠性质得到，，设，则，根据勾股定理得到，故正确；得到，故错误；连接，由内心可知平分，求得，由折叠可知，根据平行线的性质得到，求得，根据菱形的判定定理得到四边形是菱形；故正确．
本题考查解翻折变换折叠问题，等腰三角形的性质，角平分线的性质，菱形的判定，掌握相关性质定理，正确添加辅助线是解题的关键．
 

12.【答案】 

【解析】解：抛物线开口向下，
，
抛物线对称轴为直线，
，
，
抛物线与轴交点在轴上方，
，
，错误．
抛物线与轴有两个交点，
，
，错误．
，
，
由图象可得时，，
，
，正确．
时，函数取最大值，
，
，正确．
故选：．
由抛物线开口方向，对称轴位置，抛物线与轴交点位置可判断，，的符号及与的数量关系，从而判断，由抛物线与轴有两个交点可判断，由时可判断，由时取最大值判断．
本题考查二次函数图象与系数的关系，解题关键是掌握二次函数的性质，掌握二次函数与方程及不等式的关系．
 

13.【答案】 

【解析】解：，
，
．
先提取公因式，再对余下的多项式利用平方差公式继续分解．
本题考查了提公因式法，公式法分解因式，关键在于提取公因式后，可以利用平方差公式进行二次分解．
 

14.【答案】 

【解析】
共有种等可能出现的结果，其中两次都是白球的有种，
两次都摸出白球的概率是，
故答案为：．
列举出所有可能出现的结果，进而求出“两次都是白球”的概率．
本题考查了列表法与树状图法：利用列表法和树状图法展示所有可能的结果求出，再从中选出符合事件或的结果数目，求出概率．
 

15.【答案】 

【解析】解：买了甜果和苦果共一千个，
；
买甜果和苦果共花了文钱，
．
根据题意可列方程组．
故答案为：．
利用总价单价数量，结合用九百九十九文钱买了甜果和苦果共一千个，可得出关于，的二元一次方程组，此题得解．
本题考查了由实际问题抽象出二元一次方程组，找准等量关系，正确列出二元一次方程组是解题的关键．
 

16.【答案】 

【解析】解：由题意得：，，
设，则，
在中，，
，
在中，，
，
，
解得：，
，
故答案为：．
根据题意可得：，，设，则，然后在中，利用锐角三角函数的定义求出的长，再在中，利用锐角三角函数的定义求出的长，从而列出关于的方程，进行计算即可解答．
本题考查了解直角三角形的应用仰角俯角问题，熟练掌握锐角三角函数的定义是解题的关键．
 

17.【答案】 

【解析】解：，；
，；
，；
，，
．
故答案为：．
观察发现，图中第二行左边的数比第一行数的平方大，第二行右边的数第二行左边的数第一行的数第一行的数，依此规律先求，再求即可．
本题考查了规律型：数字的变化类，解答的关键是由图形得到第二行左边的数比第一行数的平方大，第二行右边的数第二行左边的数第一行的数第一行的数．
 

18.【答案】 

【解析】解：连接，作于点，
四边形是菱形，，，
，，
，
，
，
，
，
，
于，于，
，
四边形是矩形，
，
，
，
的最小值等于，
故答案为：．
连接，作于点，由菱形的性质得，，，则，由，求得，再证明四边形是矩形，则，由，得，则的最小值等于，于是得到问题的答案．
此题重点考查菱形的性质、矩形的判定与性质、勾股定理、根据面积等式求线段的长度、垂线段最短等知识与方法，正确地作出所需要的辅助线是解题的关键．
 

19.【答案】解：

，
当时，
原式

；
，
解不等式得，，
解不等式得，，
不等式组的解集为：，
把不等式组的解集在数轴上表示为：
． 

【解析】利用分式的相应的法则对式子进行整理，再代入相应的值运算即可；
利用解一元一次不等式的方法把各个不等式的解集求出来，再确定不等式组的解集即可．
本题主要考查分式的化简求值，解一元一次不等式组，解答的关键是对相应的运算法则的掌握．
 

20.【答案】解：本次调查的学生人数为人．
，
．
主题的人数为人，
主题的人数为人．
补全条形统计图如图．

设星期一至星期五分别记为，，，，，
画树状图如下：

共有种等可能的结果，其中有一天是星期五的结果有：，，，，，，，，共种，
其中有一天是星期五的概率为． 

【解析】用主题的学生人数除以其所占的百分比可得本次调查的学生人数；求出主题所占的百分比即可求得的值．
分别求出主题和主题的人数，补全条形统计图即可．
画树状图得出所有等可能的结果数以及其中有一天是星期五的结果数，再利用概率公式可得出答案．
本题考查列表法与树状图法、条形统计图、扇形统计图，能够理解条形统计图和扇形统计图，熟练掌握列表法与树状图法是解答本题的关键．
 

21.【答案】解：点在直线上，
，
即点的坐标为，
点在反比例函数的图象上，
，
反比例函数的表达式是：；

由题意得：，
解得：或，
经检验或是原方程的解，
，
点，
，
菱形是以，为边，且轴，
，
点． 

【解析】用待定系数法即可求解；
由题意得：，得到，求出的长度，进而求解．
本题考查的是反比例函数的综合运用，涉及到菱形的性质、一次函数和反比例函数的性质等，有一定的综合性，难度不大．
 

22.【答案】证明：四边形是的内接四边形，
，
，
，
，
，
，
，
平分；
解：连接并延长交于点，连接，

是的直径，
，
在中，，，
，
，
，
，
的值为． 

【解析】根据圆内接四边形对角互补以及平角定义可得，再利用等腰三角形的性质可得，然后利用同弧所对的圆周角相等可得，从而可得，即可解答；
连接并延长交于点，连接，根据直径所对的圆周角是直角可得，然后在中，利用勾股定理可求出的长，从而求出的值，最后根据同弧所对的圆周角相等可得，即可解答．
本题考查了圆周角定理，解直角三角形，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
 

23.【答案】解：设篮球的单价是元，则足球的单价是元，
由题意得：，
解得：，
经检验，是原方程的解，且符合题意，
，
答：篮球的单价是元，足球的单价是元；
设采购篮球个，则采购足球为个，
由题意得：，
解得：，
又为整数，
的值可为，，，，，，
共有种购买方案：
采购篮球个，足球个；
采购篮球个，足球个；
采购篮球个，足球个；
采购篮球个，足球个；
采购篮球个，足球个；
采购篮球个，足球个． 

【解析】设篮球的单价是元，则足球的单价是元，由题意：购买篮球的数量是足球的倍，购买篮球用了元，购买足球用了元，列出分式方程，解方程即可；
设采购篮球个，则采购足球为个，由题意：篮球多于个，且总费用低于元，列出一元一次不等式组，解不等式组，即可解决问题．
本题考查了分式方程的应用以及一元一次不等式组的应用，解题的关键是：找准等量关系，正确列出分式方程；找出数量关系，正确列出一元一次不等式组．
 

24.【答案】解：将点，代入，
，，
；

，
的直线解析式为，
当时，，
，
，
，，，
的面积的面积的面积；

，
，
设，
，，
，
，
，
，
，

或，
或，
或． 

【解析】将点，代入，即可求解；
的面积的面积的面积，即可求解；
，，，则，且，，即可求解．
本题考查二次函数的图象及性质，动点问题；要求学生能够熟练掌握二次函数解析式与相应点的求法，熟悉等腰直角三角形的性质．
 

25.【答案】解：四边形是平行四边形，
，，，
，
平分，
，
，
，
同理：，
，
；
四边形是平行四边形，
，，，
，
平分，
，
，
，
同理：，
如图所示：

点与点重合，
点与点重合，
；

分三种情况：
如图所示：

同得：，
点，，，相邻两点间的距离相等，
，
；
如图所示：

同得：，
，
；
如图所示：

同得：，
，
；
综上所述，的值为或或． 

【解析】证，得，同理，即可求解；
证，得，同理，即可求解；
分三种情况，由的结果结合点，，，相邻两点间的距离相等，分别求解即可．
本题考查了平行四边形的性质、等腰三角形的判定、平行线的性质等知识；熟练掌握平行四边形的性质和等腰三角形的判定是解题的关键．