2022-2023学年江苏省南通市通州区等两地八年级（下）期中数学试卷（含解析）

2022-2023学年江苏省南通市通州区等两地八年级（下）期中数学试卷

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1.  已知▱中，，则的度数为(    )

A.  B.  C.  D.

2.  下列长度的三条线段能首尾相接构成直角三角形的是(    )

A. ，， B. ，， C. ，， D. ，，

3.  在下列条件中，能够判定▱为菱形的是(    )

A.  B.  C.  D.

4.  如图，一棵垂直于地面的树在一次强台风中从高地面米处折断倒下，倒下部分与地面成角，这棵树在折断前的高度为(    )

A. 米 B. 米 C. 米 D. 米

5.  如图，在中，是斜边上的中线若，则的度数为(    )

A.
B.
C.
D.

6.  已知函数是正比例函数，则常数的值为(    )

A.  B.  C.  D.

7.  若，则函数的图象可能是(    )

A.  B.
C.  D.

8.  如图，四边形是正方形，点是上的任意一点，于点于点，已知，，则线段的长为(    )

A.
B.
C.
D.

9.  如图，直线与的交点横坐标为，则关于的不等式组的整数解为(    )

A.  B.  C.  D.

10.  已知直线与直线，且，若两直线与轴围成的三角形面积为，则的值是(    )

A.  B.  C.  D.

二、填空题（本大题共8小题，共30.0分）

11.  将直线的向上平移个单位，则平移后的直线解析式是______ ．

12.  已知菱形的两条对角线长分别是和，则这个菱形的面积为______．

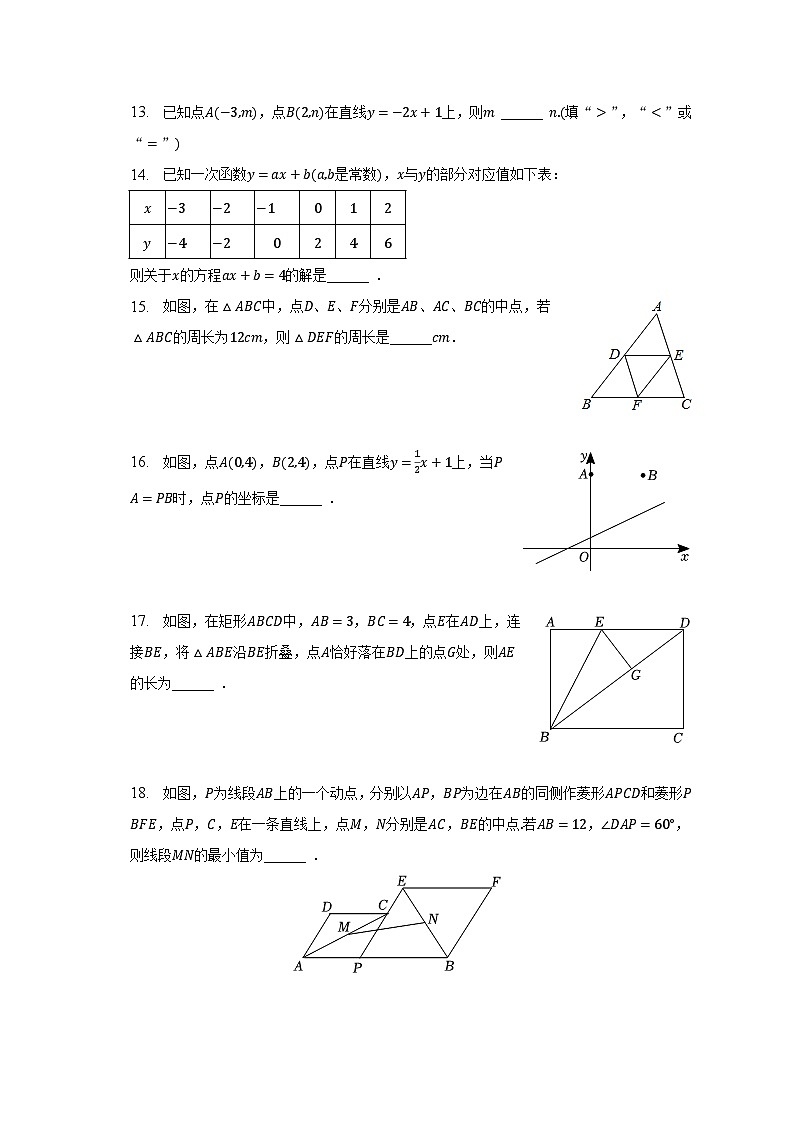
13.  已知点，点在直线上，则 ______ 填“”，“”或“”

14.  已知一次函数是常数，与的部分对应值如下表：

则关于的方程的解是______ ．

15.  如图，在中，点、、分别是、、的中点，若的周长为，则的周长是______．

16.  如图，点，，点在直线上，当时，点的坐标是______ ．

17.  如图，在矩形中，，，点在上，连接，将沿折叠，点恰好落在上的点处，则的长为______ ．

18.  如图，为线段上的一个动点，分别以，为边在的同侧作菱形和菱形，点，，在一条直线上，点，分别是，的中点若，，则线段的最小值为______ ．

三、解答题（本大题共8小题，共90.0分。解答应写出文字说明，证明过程或演算步骤）

19.  本小题分
已知一次函数的图象经过和两点．
求这个一次函数的解析式；
当时，求的值．

20.  本小题分
如图，，平分交于点，交于点．
求证：四边形是菱形．

21.  本小题分
如图，在中，，，是边上的中线，且，延长到点，使，连接．
求证：是直角三角形．
求边的长．

22.  本小题分
暑期将至，某健身俱乐部面向学生推出暑期优惠活动，活动方案如下．
方案一：购买一张元的学生暑期专享卡，每次健身费用元；
方案二：不购买学生暑期专享卡，每次健身费用元．
设健身次数为次，所需费用为元，分别就两种活动方案写出关于的函数解析式；
当学生消费次数在什么范围时，选择方案一更划算？

23.  本小题分
已知四边形是矩形，是等边三角形，请仅用无刻度直尺按下列要求画图，并保留画图痕迹画图过程用虚线表示，画图结果用实线表示．
在图中，作的平分线；
在图中，作菱形，使，，，四点均在矩形的各边上．
 

24.  本小题分
如图，，两地相距，在，之间有汽车站站客车由地驶向站、货车由地驶向地，两车同时出发，匀速相向行驶图是客车、货车离站的路程单位：与行驶时间单位：之间的函数关系图象．
客车的速度为______ ，货车的速度为______ ；
求两小时后，货车离站的路程与行驶时间之间的函数关系式；
求图中点的坐标．
 

25.  本小题分
在一次数学研究性学习中，小敏将两个全等的直角三角形纸片和拼在一起，使点与点重合，点与点重合如图，其中，，，并进行如下研究活动，将图中的纸片沿方向平移，连结，如图，当点与点重合时停止平移．

图中的四边形是平行四边形吗？请说明理由．
当纸片平移到某一位置时，小敏发现四边形为矩形如图，求的长．

26.  本小题分
在平面直角坐标系中，对于点和，给出如下定义：如果，那么称点为点的“联络点”例如，点的“联络点”为，点的“联络点”为点．
若点是直线上点的“联络点”，求的值；
若点是直线上点的“联络点”，求点的坐标；
已知直线与轴交于点，该直线上的一点的“联络点”为点若的面积为，求线段的长．

答案和解析

1.【答案】 

【解析】解：如图，四边形是平行四边形，
，
，
．

故选：．
根据平行四边形的性质：对角相等，即可得出答案．
本题考查了平行四边形的性质，解题的关键是记住平行四边形的性质，属于中考基础题．
 

2.【答案】 

【解析】解：、，，
，
不能构成直角三角形，
故A不符合题意；
B、，，
，
能构成直角三角形，
故B符合题意；
C、，，
，
不能构成直角三角形，
故C不符合题意；
D、，，
，
不能构成直角三角形，
故D不符合题意；
故选：．
根据勾股定理的逆定理进行计算，逐一判断即可解答．
本题考查了勾股定理的逆定理，熟练掌握勾股定理的逆定理是解题的关键．
 

3.【答案】 

【解析】解：、由，不能判定▱为菱形，故选项A不符合题意；
B、由，能判定▱为矩形，不能判定▱为菱形，故选项B不符合题意；
C、由，不能判定▱为菱形，故选项C不符合题意；
D、由，能判定▱为菱形，故选项D符合题意；
故选：．
由菱形的判定和矩形的判定分别对各个选项进行判断即可．
本题考查了菱形的判定、平行四边形的判定以及矩形的判定，熟练掌握菱形的判定是解题的关键．
 

4.【答案】 

【解析】解：，，，
，
这棵树在折断前的高度为米．
故选：．
根据含有角的直角三角形的性质可以得到的长，然后即可计算出的值，从而可以得到这棵树在折断前的高度．
本题考查了含有角的直角三角形的性质，熟练掌握性质是解题的关键．
 

5.【答案】 

【解析】解：在中，是斜边上的中线，
，
，
，
，
故选：．
根据直角三角形斜边上的中线性质可得，从而可得，然后利用角的和差关系进行计算即可解答．
本题考查了直角三角形斜边上的中线，熟练掌握直角三角形斜边上的中线性质是解题的关键．
 

6.【答案】 

【解析】解：函数是正比例函数，
，
解得．
故选：．
先根据正比例函数的定义列出关于的方程组，求出的值即可．
本题考查的是正比例函数的定义，即形如的函数叫正比例函数．
 

7.【答案】 

【解析】

【分析】
根据，可知，或，，然后分情况讨论直线的位置关系．
本题考查一次函数的图象性质，解题的关键是正确理解与对直线位置的影响，属于基础题型．
【解答】
解：由题意可知：可知，或，，
当，时，
直线经过一、二、三象限，
当，
直线经过二、三、四象限，
故选：．  

8.【答案】 

【解析】解：四边形是正方形，，，
，，
，
在和中，
，
≌，
，，
．
故选：．
证明≌，得，，进而可以解决问题．
本题主要考查了正方形性质、全等三角形的判定与性质，证明≌是解答本题的关键．
 

9.【答案】 

【解析】解：直线与的交点的横坐标为，
关于的不等式的解集为，
时，，
的解集是，
的解集是，
关于的不等式的整数解为．
故选：．
满足不等式就是直线位于直线的上方且位于轴的上方的图象，据此求得自变量的取值范围即可．
本题考查了一次函数的图象和性质以及与一元一次不等式的关系，要熟练掌握．
 

10.【答案】 

【解析】解：联立两直线解析式得：，
解得两直线交点的横坐标为，
直线与轴的交点坐标为，
直线与轴的交点坐标为，
两交点的距离为，
两直线与轴围成的三角形面积为，
，
．
故选：．
联立两直线解析式可求得两直线交点的横坐标为，再求出两直线与轴的交点坐标，算出两交点间的距离为，以此可得，以此计算即可求解．
本题主要考查一次函数图象上点的坐标特征、直线与坐标轴围成图形的面积，联立两直线解析式得到两直线交点的横坐标为是解题关键．
 

11.【答案】 

【解析】解：将直线向上平移个单位长度，所得直线的解析式为，
故答案为：．
直接根据“上加下减”的平移规律求解即可．
本题考查一次函数的图象与几何变换，在平面直角坐标系中，平移后解析式有这样一个规律“左加右减，上加下减”．
 

12.【答案】 

【解析】解：菱形的两条对角线长分别是和，
这个菱形的面积为
故答案为
因为菱形的面积为两条对角线积的一半，所以这个菱形的面积为．
此题考查了菱形面积的求解方法：底乘以高，对角线积的一半．
 

13.【答案】 

【解析】解：点，点在直线上，
当时，；
当时，，
，
．
故答案为：．
直接把点，点代入直线，求出，的值，再比较大小即可．
本题考查的是一次函数图象上点的坐标特点，熟知一次函数图象上各点的坐标一定适合此函数的解析式是解题的关键．
 

14.【答案】 

【解析】解：根据图表可得：当时，，即时，，
因而方程的解是．
故答案为：．
方程的解为时函数的的值，根据图表即可得出此方程的解．
本题主要考查了一次函数与一元一次方程，正确数形结合分析是解题关键．
 

15.【答案】 

【解析】解：点、、分别是、、的中点，
，，，
的周长．
故答案为：．
根据三角形中位线定理易得所求的三角形的各边长为原三角形各边长的一半，那么所求的三角形的周长就等于原三角形周长的一半．
此题考查的是三角形中位线的性质，即三角形的中位线平行于第三边且等于第三边的一半．
 

16.【答案】 

【解析】解：点在直线上，
设点的坐标为．
，
，
即，
解得：，
点的坐标为
故答案为：
设点的坐标为，利用两点间的距离结合，即可得出关于的一元一次方程，解之即可得出结论．
本题考查了一次函数图象上点的坐标特征、两点间的距离以及解一元一次方程，利用一次函数图象上点的坐标特征及两点间的距离，找出关于的方程是解题的关键．
 

17.【答案】 

【解析】解：四边形是矩形，，，
，，
，
由折叠得，，，
，，
，且，
，
，
故答案为：．
先由，，，根据勾股定理求得，再由折叠得，，，则，，在中根据勾股定理得，则，求得．
此题重点考查矩形的性质、轴对称的性质、勾股定理等知识，在中根据勾股定理列方程是解题的关键．
 

18.【答案】 

【解析】解：连接、．

四边形，四边形是菱形，，
，，
，分别是对角线，的中点，
，，
，
设，则，，，
，
时，有最小值，最小值为，
故答案为：．
连接、首先证明设，则，，，构建二次函数，利用二次函数的性质即可解决问题．
本题考查了梯形中位线的性质，菱形的性质、勾股定理、二次函数的性质等知识，解题的关键是学会添加常用辅助线，构建二次函数解决最值问题．
 

19.【答案】解把和两点坐标代入中得，
，
解得，
一次函数的解析式为：．
当时，，
当时，的值为． 

【解析】把和两点坐标代入中，建立方程组，求出，的值即可得结果．
令中求得的解析式中，求出即可．
本题考查了待定系数法求一次函数解析式以及知自变量的值求函数值，熟练掌握待定系数法是解题关键．
 

20.【答案】证明：，，
四边形是平行四边形，
，
，
平分，
，
，
，
四边形是菱形； 

【解析】根据平行四边形的判定定理得到四边形是平行四边形，根据平行线的性质得到，根据角平分线的定义得到，得到，根据菱形的判定定理得到四边形是菱形．
本题考查了菱形的判定定理，平行四边形 的判定和性质，角平分线的定义，熟练掌握菱形的判定定理是解题的关键．
 

21.【答案】证明：在和中，

≌，
，
  

是直角三角形．
    
解：在中，

． 

【解析】首先证明≌，推出，由，推出是直角三角形．
在中，求出，根据即可解决问题．
本题考查全等三角形的判定和性质、勾股定理以及勾股定理的逆定理等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
 

22.【答案】解：由题意得：方案一：，
方案二：，
方案一所需费用为与健身次数为的函数关系式为，方案一所需费用为与健身次数为的函数关系式为；
由题意得：，
解得：，
学生消费次数大于次时，选择方案一更划算． 

【解析】根据两种活动方案的收费标准即可求解；
要选择方案一更划算，则方案一所花费用小于方案二所花费用，以此列出不等式，求解即可．
本题主要考查一次函数的应用、一元一次不等式的应用，读懂题意，找准题目所蕴含的等量关系，并正确列出函数关系式是解题关键．
 

23.【答案】解：如图中，射线即为所求；
如图中，四边形即为所求．
 

【解析】连接，交于点，连接，射线即为所求；
构造矩形的中点四边形即可．
本题考查作图复杂作图，角平分线的定义，菱形的判定，矩形的性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
 

24.【答案】   

【解析】解：由图象可得：货车从地驶向站花费了小时，行驶了，
则货车的速度为，
地与站的距离为，
客车的速度为；
故答案为：，；
由知，货车的速度为，
小时后货车的行驶时间为小时，
；
设，
因为，在的函数图象上，
，
解得：，
，
联立得：，
解得：，
点的坐标为．
根据题意并结合图象可知，货车从地驶向站花费了小时，行驶了，根据“速度路程时间”即可求出货车的速度；再算出地与站的距离，由图象可知客车从地驶向站花费了小时，根据“速度路程时间”即可求出客车的速度；
根据“路程速度时间”即可求解；
根据待定系数法先求出关于的函数解析式，再联立所求的函数关系式，求解即可．
本题主要考查一次函数的应用、用待定系数法求一次函数解析式，解题关键联立两函数解析式得出方程组，求得点的坐标．
 

25.【答案】解：四边形是平行四边形．
证明：，
，，
，
四边形是平行四边形；
如图，连接交于点，

四边形为矩形，
，
设，则，
，
在中，，
，
解得：，
． 

【解析】由全等三角形的性质得出，，则，可得出结论；
连接交于点，设，则，得出，由勾股定理列出方程，进而求解．
本题是四边形综合题，考查了平行四边形的判定与性质，平移的性质，矩形的性质，全等三角形的判定与性质，勾股定理，平行线的判定与性质等知识，熟练掌握全等三角形的判定与性质是解题的关键．
 

26.【答案】解：由题意得：，
，
解得：；
当时，，由题意得：，解得，
当时，，由题意得：，解得，
设，
的面积为，
，
，
直线与轴交于点，
，
，
解得：，或不合题意，舍去，
，
． 

【解析】根据新定义求解；
分类讨论，先根据新定义写出的坐标，利用待定系数法求解；
先求出的坐标，再用表示和的坐标，根据三角形的面积公式求出，最后根据两点间的距离公式求解．
本题考查了一次函数图象上点的坐标特征，理解新定义是解题的关键．