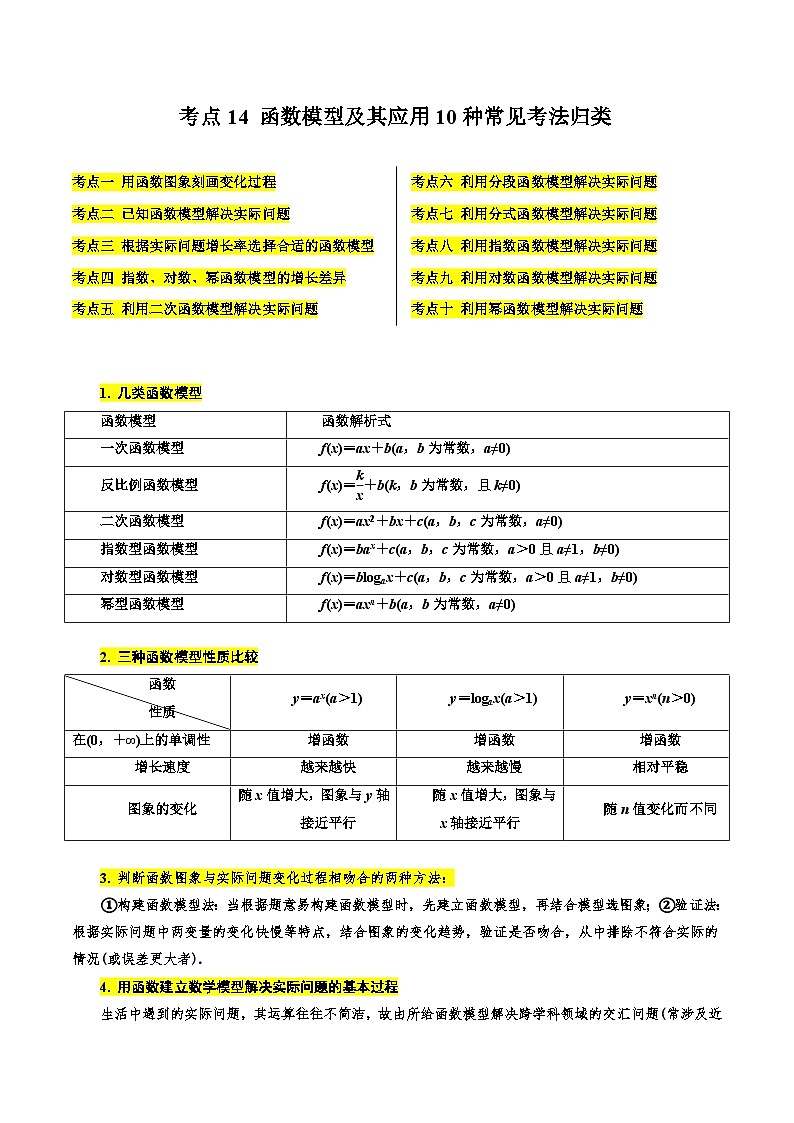
考点14 函数模型及其应用10种常见考法归类-备战高考数学一轮题型归纳与解题策略(新高考地区专用)

这是一份考点14 函数模型及其应用10种常见考法归类-备战高考数学一轮题型归纳与解题策略(新高考地区专用)，文件包含考点14函数模型及其应用10种常见考法归类解析版docx、考点14函数模型及其应用10种常见考法归类原卷版docx等2份试卷配套教学资源，其中试卷共59页， 欢迎下载使用。

考点14 函数模型及其应用10种常见考法归类


考点一 用函数图象刻画变化过程
考点二 已知函数模型解决实际问题
考点三 根据实际问题增长率选择合适的函数模型
考点四 指数、对数、幂函数模型的增长差异
考点五 利用二次函数模型解决实际问题
考点六 利用分段函数模型解决实际问题
考点七 利用分式函数模型解决实际问题
考点八 利用指数函数模型解决实际问题
考点九 利用对数函数模型解决实际问题
考点十 利用幂函数模型解决实际问题


1. 几类函数模型
函数模型
函数解析式
一次函数模型
f(x)＝ax＋b(a，b为常数，a≠0)
反比例函数模型
f(x)＝＋b(k，b为常数，且k≠0)
二次函数模型
f(x)＝ax2＋bx＋c(a，b，c为常数，a≠0)
指数型函数模型
f(x)＝bax＋c(a，b，c为常数，a＞0且a≠1，b≠0)
对数型函数模型
f(x)＝blogax＋c(a，b，c为常数，a＞0且a≠1，b≠0)
幂型函数模型
f(x)＝axn＋b(a，b为常数，a≠0)

2. 三种函数模型性质比较
函数
性质
y＝ax(a＞1)
y＝logax(a＞1)
y＝xn(n＞0)
在(0，＋∞)上的单调性
增函数
增函数
增函数
增长速度
越来越快
越来越慢
相对平稳
图象的变化
随x值增大，图象与y轴
接近平行
随x值增大，图象与x轴接近平行
随n值变化而不同

3. 判断函数图象与实际问题变化过程相吻合的两种方法：
①构建函数模型法：当根据题意易构建函数模型时，先建立函数模型，再结合模型选图象；②验证法：根据实际问题中两变量的变化快慢等特点，结合图象的变化趋势，验证是否吻合，从中排除不符合实际的情况(或误差更大者).
4. 用函数建立数学模型解决实际问题的基本过程
生活中遇到的实际问题，其运算往往不简洁，故由所给函数模型解决跨学科领域的交汇问题(常涉及近似计算)是近几年高考热点问题，解此类问题的关键点：
(1)分析和理解实际问题的增长情况(是“对数增长”“直线上升”还是“指数爆炸”或其他)；
(2)根据增长情况选择函数类型构建数学模型，将实际问题化归为数学问题；
(3)通过运算、推理求解函数模型，根据已知条件，利用待定系数法确定模型中的待定系数；,
(4)用得到的函数模型描述实际问题的变化规律、解决有关问题.
注：解函数应用问题的步骤：
(1)审题：弄清题意，识别条件与结论，弄清数量关系，初步选择数学模型；
(2)建模：将自然语言转化为数学语言，将文字语言转化为符号语言，利用已有知识建立相应的数学模型;
(3)解模：求解数学模型，得出结论；
(4)还原：将数学问题还原为实际问题．
5. 二次函数模型解析式的选择策略
根据已知条件确定二次函数解析式，一般用待定系数法，选择规律如下：

6. 分段函数模型的求解策略
在现实生活中，很多问题的两变量之间的关系，不能用同一个关系式给出，而是由几个不同的关系式构成分段函数．如出租车票价与路程之间的关系，就是分段函数．分段函数主要是每一段上自变量变化所遵循的规律不同，可以先将其作为几个不同问题，将各段的规律找出来，再将其合在一起．要注意各段变量的范围，特别是端点．构造分段函数时，要力求准确、简捷，做到分段合理、不重不漏．分段函数的最值是各段最大值(或最小值)中的最大者(或最小者)．
7. 指数、对数函数模型的求解策略
(1)指数函数模型，常与增长率相结合进行考查，在实际问题中有人口增长、银行利率、细胞分裂等增长问题可以利用指数函数模型来表示．
(2)应用指数函数模型时，关键是对模型的判断，先设定模型将有关数据代入验证，确定参数，从而确定函数模型．
(3)y＝a(1＋x)n通常利用指数运算与对数函数的性质求解．
(4)对于直线上升、指数增长、对数增长的特点要注意区分：
与指数函数、对数函数两类函数模型有关的实际问题，在求解时，要先学会合理选择模型，在两类模型中，指数函数模型是增长速度越来越快(底数大于1)的一类函数模型，与增长率、银行利率有关的问题都属于指数函数模型．
直线上升：匀速增长，其增长量固定不变；指数增长：先慢后快，其增长量成倍增加，常用“指数爆炸”来形容；对数增长：先快后慢，其增长速度缓慢．公司的利润选择直线上升或指数模型增长，而员工奖金选择对数模型增长．
(5)在解决指数函数、对数函数模型问题时，一般需要先通过待定系数法确定函数解析式，再借助函数的图象求解最值问题，必要时可借助导数．


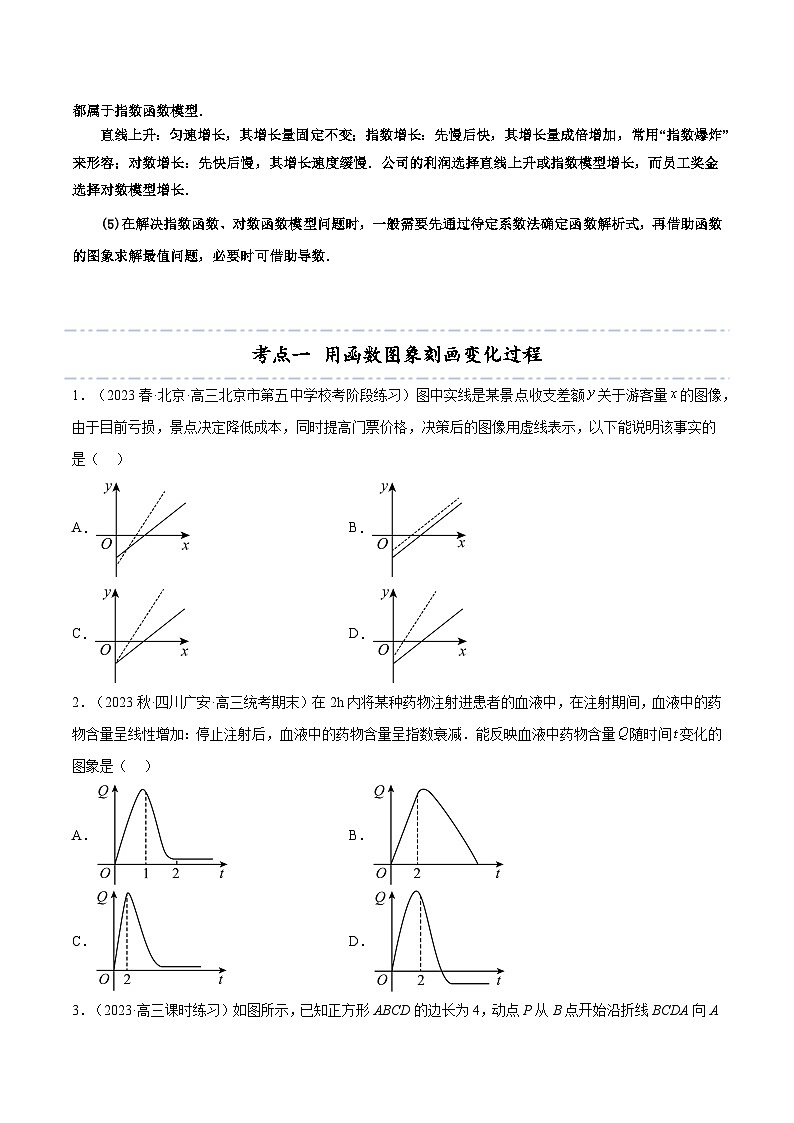
考点一 用函数图象刻画变化过程
1．（2023春·北京·高三北京市第五中学校考阶段练习）图中实线是某景点收支差额关于游客量的图像，由于目前亏损，景点决定降低成本，同时提高门票价格，决策后的图像用虚线表示，以下能说明该事实的是（    ）
A． B．
C． D．
【答案】D
【分析】根据直线的纵截距表示成本，倾斜角与门票价格的关系判断.
【详解】对于A，当时，虚线值减小，说明成本提高了，不满足题意，A错误；
对于B，两函数图象平行，说明票价不变，不合题意，B错误；
对于C，当时， 值不变，说明成本不变，不满足题意，C错误；
对于D，当时，虚线值变大，说明成本见减小，又因为虚线的倾斜角变大，
说明提高了门票的价格，符合题意，D正确，
故选:D.
2．（2023秋·四川广安·高三统考期末）在2h内将某种药物注射进患者的血液中，在注射期间，血液中的药物含量呈线性增加：停止注射后，血液中的药物含量呈指数衰减．能反映血液中药物含量随时间变化的图象是（    ）
A． B．
C． D．
【答案】C
【分析】根据在注射期间，血液中的药物含量呈线性增加；停止注射后，血液中的药物含量呈指数衰减即可得出．
【详解】在注射期间，血液中的药物含量呈线性增加，则第一段图象为线段，且为增函数，排除A，D，
停止注射后，血液中的药物含量呈指数衰减．排除B．
能反映血液中药物含量随时间变化的图象是C．
故选：C．
3．（2023·高三课时练习）如图所示，已知正方形ABCD的边长为4，动点P从B点开始沿折线BCDA向A点运动．设P点运动的路程为x，△ABP的面积为S，则函数S＝f(x)的图像是(    )

A． B．
C． D．
【答案】D
【分析】数形结合，分P点在BC、CD、DA三种情况，依次求出S＝f(x)的解析式，根据解析式即可作出图像﹒
【详解】由题意：
P点在BC上时，0≤x＜4，S＝＝2x；
P点在CD上时，4≤x≤8，S＝＝8；
P点在DA上时，8＜x≤12，S＝24－2x．
故选：D﹒
4．（2023·全国·高三专题练习）已知正四面体的棱长为，为棱上的动点（端点、除外），过点作平面垂直于，与正四面体的表面相交．记，将交线围成的图形面积表示为的函数，则的图象大致为（    ）
A． B．
C． D．
【答案】C
【分析】取线段的中点，连接、，证明出平面，分析可知平面与平面平行或重合，分、、三种情况讨论，计算出的面积，利用三角形相似可得出的表达式，即可得出合适的选项.
【详解】取线段的中点，连接、，
因为、为等边三角形，为的中点，则，，
，、平面，平面，
因为平面，所以，平面与平面平行或重合，
且，
取的中点，连接，则，
且，故.
①当时，平面平面，平面平面，
平面平面，，同理可知，，，
所以，，故，
如下图所示：

则，则；
②当时，；
③当时，平面平面，平面平面，
平面平面，，同理可知，，，
所以，，故，
如下图所示：

则，则.
综上所述，，故函数的图象如C选项中的图象.
故选：C.
【点睛】关键点点睛：本题考查函数图象的识别，解题的关键对分类讨论，求出函数的解析式，进而辨别出函数的图象.
考点二 已知函数模型解决实际问题
5．（2023·河南商丘·商丘市实验中学校联考模拟预测）已知电磁波在空间中自由传播时的损耗公式为，其中D为传输距离（单位：km），F为载波频率（单位：MHz），L为传输损耗（单位：dB）．若载波频率变为原来的200倍，传输损耗增加90dB，则传输距离约为原来的（    ）参考数据：．
A．倍 B．倍 C．倍 D．倍
【答案】B
【分析】设出变化前后的相关量，再结合已知列式，借助对数运算求解作答.
【详解】设原来的传输损耗、载波频率、传输距离分别为，
变化后的传输损耗、载波频率、传输距离分别为，
则，，
因此，
于是，解得
所以传输距离约为原来的倍.
故选：B
6．（2023·北京通州·统考模拟预测）声强级（单位：）与声强x（单位：）满足．一般噪音的声强级约为80，正常交谈的声强级约为50，那么一般噪音的声强约为正常交谈的声强的（    ）
A．倍 B．倍 C．倍 D．倍
【答案】A
【分析】根据题中公式，分别求出一般噪音的声强和正常交谈的声强，从而可得出答案.
【详解】当时，即，解得，
即一般噪音的声强约，
当时，即，解得，
即正常交谈的声强约，
所以一般噪音的声强约为正常交谈的声强的倍.
故选：A.
7．（2023春·湖南·高三校联考阶段练习）住房的许多建材都会释放甲醛.甲醛是一种无色、有着刺激性气味的气体，对人体健康有着极大的危害.新房入住时，空气中甲醛浓度不能超过0.08，否则，该新房达不到安全入住的标准.若某套住房自装修完成后，通风周与室内甲醛浓度y（单位：）之间近似满足函数关系式，其中，且，，则该住房装修完成后要达到安全入住的标准，至少需要通风（    ）
A．17周 B．24周 C．28周 D．26周
【答案】D
【分析】由已知数据求得参数，然后解不等式即可得．
【详解】，由，，得，，
两式相减得，则，所以，.
该住房装修完成后要达到安全入住的标准，则，
则，即，解得，
故至少需要通风26周.
故选：D．
8．（2023春·陕西榆林·高三绥德中学校考阶段练习）昆虫信息素是昆虫用来表示聚集、觅食、交配、警戒等信息的化学物质，是昆虫之间起化学通讯作用的化合物，是昆虫交流的化学分子语言，包括利它素、利己素、协同素、集合信息素、追踪信息素、告警信息素、疏散信息素、性信息素等．人工合成的昆虫信息素在生产中有较多的应用，尤其在农业生产中的病虫害的预报和防治中较多使用．研究发现，某昆虫释放信息素t秒后，在距释放处x米的地方测得的信息素浓度y满足，其中k，a为非零常数．已知释放信息素1秒后，在距释放处2米的地方测得信息素浓度为m；若释放信息素4秒后，距释放处b米的位置，信息素浓度为，则b＝（    ）
A．3 B．4 C．5 D．6
【答案】B
【分析】根据已知的浓度解析式，代入变量，结合对数的运算，化简求值.
【详解】由题意，，
所以），
即．又，所以．
因为，所以．
故选：B．
9．（2023秋·北京朝阳·高三统考期末）2023年10月31日，长征五号B遥四运载火箭带着中华民族千百年来探索浩瀚宇宙的梦想，将中国空间站梦天实验舱准确送入预定轨道在不考虑空气阻力的条件下，若火箭的最大速度v（单位：）和燃料的质量M（单位：t）、火箭（除燃料外）的质量m（单位：t）的关系满足，M，m，v之间的关系如图所示，则下列结论正确的是（    ）

A．当时， B．当时，
C．当时， D．当时，
【答案】C
【分析】由题及图象关系可知，在中，当一定时，越大，则越大，
当一定时，越小，则越大，代入对应的，逐项判断选项即可得到答案.
【详解】由题及图象关系可知，在中，当一定时，越大，则越大，
当一定时，越小，则越大，
对于A，当时，，故A错误.
对于B，当时，，故B错误.
对于C，当时，，故C正确.
对于D，因为，令,， ，故D错误.
故选：C.
10．【多选】（2023·全国·高三专题练习）某医药研究机构开发了一种新药，据监测，如果患者每次按规定的剂量注射该药物，注射后每毫升血液中的含药量y（微克）与时间t（小时）之间的关系近似满足如图所示的曲线．据进一步测定，当每毫升血液中含药量不少于0.125微克时，治疗该病有效，则（    ）

A．
B．注射一次治疗该病的有效时间长度为6小时
C．注射该药物小时后每毫升血液中的含药量为0.4微克
D．注射一次治疗该病的有效时间长度为时
【答案】AD
【分析】利用图象分别求出两段函数解析式，再进行逐个分析，即可解决．
【详解】由函数图象可知，
当时，，即，解得，
，故正确，
药物刚好起效的时间，当，即，
药物刚好失效的时间，解得，
故药物有效时长为小时，
药物的有效时间不到6个小时，故错误，正确；
注射该药物小时后每毫升血液含药量为微克，故错误，
故选：．
考点三 根据实际问题增长率选择合适的函数模型
11．（2023·高三单元测试）下表显示出函数值随自变量变化的一组数据，由此可判断它最可能的函数模型为（    ）
x
-2
-1
0
1
2
3
y

0.26
1.11
3.96
16.05
63.98

A．一次函数模型 B．二次函数模型
C．对数函数模型 D．指数函数模型
【答案】D
【分析】利用各类型函数的特点，取点，设出函数解析式，代入其他对应值验证即可求解.
【详解】由变量可取负数，故函数模型暂排除对数函数模型；故C错误；
取点，
设一次函数，则
，解得，即，
而当时，，所以不是一次函数模型；故A错误；
设二次函数，则
  解得 ，即.
当时，，故不满足题意；故B错误；
设指数函数，则
，解得，即，
代入其他值，验证：接近；接近；接近；接近，故D正确.
故选：D .
12．（2023秋·高三单元测试）下列函数中，随着的增大，增长速度最快的是（    ）
A． B．
C． D．
【答案】D
【分析】根据不同函数增长的差异直接判断即可.
【详解】A选项是常数函数，B选项是一次函数，C、D选项都是指数型函数，
C选项的指数型函数的底数是2，D选项的指数型函数的底数是，且，
所以随着的增大，增长速度最快的是D.
故选：D.
13．（2023秋·浙江·高三校联考期末）有一组实验数据如下表所示：
t
3.0
6.0
9.0
12.0
15.0
v
1.5
2.5
2.9
3.6
4.0
现准备用下列函数中的一个近似地表示这些数据满足的规律，其中最接近的一个是（    ）
A． B． C． D．
【答案】D
【分析】根据题设中表格中的数据画出散点图，结合图象和选项，得到答案.
【详解】由表格中的数据，作出数据的散点图，如图所示，

数据散点图和对数函数的图象类似，所以选项D最能反映之间的函数关系.
故选：D.
14．（2023秋·重庆九龙坡·高三统考期末）某同学参加研究性学习活动，得到如下实验数据：

3
9
27
81

2



以下函数中最符合变量与的对应关系的是（    ）
A． B．
C． D．
【答案】D
【分析】根据表格给出的数据，函数的增长速度越来越慢，再依次判断每个选项函数的增长速度得到答案.
【详解】根据表格给出的数据，函数的增长速度越来越慢，
对选项A：增长速度不变，不满足；
对选项B：时，增长速度越来越大，不满足；
对选项C：时，增长速度越来越大，不满足；
对选项D：函数的增长速度越来越慢，满足.
故选：D
15．（2023·高三课时练习）已知三个变量，，随变量的变化数据如下表：

1
2
4
6
8
…

2
4
16
64
256
…

1
4
16
36
64
…

0
1
2
2.585
3
…
则反映，，随x变化情况拟合较好的一组函数模型是（　　）
A．，， B．，，
C．，， D．，，
【答案】B
【分析】根据指数函数、幂函数与对数函数图像变化的性质可得.
【详解】从题表可以看出，三个变量，，都随x的增大而增大，但是增长速度不同，其中变量的增长呈指数函数型变化，变量的增长呈幂函数型变化，变量的增长呈对数函数型变化．
此外，也可以使用第五组数据代入检验得到答案.
故选：B.
16．（2023秋·贵州黔东南·高三统考期末）1766年人类已经发现太阳系中的行星有金星、地球、火星、木星和土星．科学家在研究了各行星离太阳的距离（单位：，是天文学中计量天体之间距离的一种单位）的排列规律后，预测在火星和木星之间应该还有一颗未被发现的行星（后被命名为谷神星）存在，并按离太阳的距离从小到大列出了如下表所示的数据：

行星编号
1（金星）
2（地球）
3（火星）
4（    ）
5（木星）
6（土星）
离太阳的距离






(1)为了描述行星离太阳的距离与行星编号之间的关系，根据表中已有的数据画出散点图，并根据散点图的分布状况，从以下三种模型中选出你认为最符合实际的一种函数模型（直接给出结论）；
①；②；③．
(2)根据你的选择，依表中前三组数据求出函数解析式，并用剩下的两组数据检验模型的吻合情况；（误差小于0.2的为吻合）
(3)请用你求得的模型，计算谷神星离太阳的距离．
【答案】(1)散点图见解析，模型②符合题意
(2)，模型与数据吻合
(3)
【分析】（1）根据已知作出散点图，根据散点图结合所给函数模型图像性质得出答案；
（2）将三点代入所选函数模型，求出参数，在根据后两点验证即可；
（3）根据（2）求出的函数模型，令，即可求出.
【详解】（1）散点图如图所示：

根据散点图可知，模型②符合题意；
（2）将，，分别代入，
得，解得，，
所以
当时，，误差，吻合，
当时，，误差，吻合，
所以，模型与数据吻合；
（3）当时，，
即谷神星距太阳的距离为.
考点四 指数、对数、幂函数模型的增长差异
17．（2023·全国·高三专题练习）下列函数中，随着的增大，函数值的增长速度最快的是(    )
A． B． C． D．
【答案】D
【分析】根据指对幂函数的增长速度即可判断.
【详解】当x＞1时，指数函数增长最快，幂函数其次，对数函数最慢，故函数的增长速度最快．
故选：D.
18．【多选】（2023秋·广东广州·高三广东实验中学校考期中）已知函数，，，下列关于这三个函数的描述中，当在上逐渐增大时，下列说法正确的是（    ）
A．的增长速度越来越快 B．的增长速度越来越快
C．的增长速度一直快于 D．的增长速度有时慢于
【答案】BD
【分析】在同一坐标系中画出3个函数图象，然后根据图象逐个分析判断即可.
【详解】在同一平面直角坐标系中画出函数，，的图象，如图所示，

由图可知的增长速度没有变，所以A错误，
在上的增长速度越来越快，所以B正确，
由图可知在上的增长速度最慢，而在上的增长速度最快，所以C错误，D正确，
故选：BD
19．【多选】（2023秋·高三单元测试）函数，，，在区间上（    ）
A．递减速度越来越慢 B．递减速度越来越慢
C．递减速度越来越慢 D．的递减速度慢于递减速度
【答案】ABC
【分析】根据指数函数，对数函数及幂函数的性质即得.
【详解】根据指数函数，对数函数及幂函数的性质结合图象可知在区间上，

递减速度越来越慢，故A正确；
递减速度越来越慢，故B正确；
递减速度越来越慢，故C正确；
的递减速度慢于递减速度，故D错误.
故选：ABC.
20．（2023春·江苏南通·高三南通一中校考阶段练习）已知，则下列命题中正确的是（    ）
A．，，有成立
B．，，有成立
C．，，有成立
D．，，有成立
【答案】A
【分析】根据不同函数类型的增长速度，即可得到答案.
【详解】因为，所以函数、、均为单调递增函数.
而且各类函数的增长速度为：指数函数快于幂函数，幂函数快于对数函数.
所以，，，有成立.
故选：A.
21．（2023·高三课时练习）若，则使成立的的取值范围是________，使成立的的取值范围是________．
【答案】
【分析】画出指对幂函数的图象，数形结合法判断不等关系下对应x的范围即可.
【详解】在同一平面直角坐标系中作出，，在上的图象如下．

由图得，若，则，
若，则或．
故答案为：，
考点五 利用二次函数模型解决实际问题
22．（2023·全国·高三专题练习）某小型服装厂生产一种风衣，日销售量x（件）与单价P（元）之间的关系为，生产x件所需成本为C（元），其中，若要求每天获利不少于1300元，则日销量x的取值范围是（    ）
A．， B．，
C．， D．，
【答案】B
【分析】由题意求得利润函数，然后解不等式即可得．
【详解】由题意日销量x件时，利润是，
，，．
故选：B．
23．（2023·全国·高三专题练习）劳动实践是大学生学习知识､锻炼才干的有效途径，更是大学生服务社会､回报社会的一种良好形式某大学生去一服装厂参加劳动实践，了解到当该服装厂生产的一种衣服日产量为x件时，售价为s元/件，且满足，每天的成本合计为元，请你帮他计算日产量为___________件时，获得的日利润最大，最大利润为___________万元.
【答案】 200 7.94
【分析】将利润表示为关于的一个二次函数，求出该函数的最值即可.
【详解】由题意易得日利润，
故当日产量为200件时，获得的日利润最大，最大利润为7.94万元，
故答案为：200，7.94.
24．（2023·全国·高三专题练习）某企业生产，两种产品，根据市场调查和预测，产品的利润（万元）与投资额（万元）成正比，其关系如图（1）所示；产品的利润（万元）与投资额（万元）的算术平方根成正比，其关系如图（2）所示．

(1)分别将，两种产品的利润表示为投资额的函数；
(2)该企业已筹集到10万元资金，并全部投入，两种产品的生产，问：怎样分配这10万元投资，才能使企业获得最大利润？其最大利润约为多少万元（精确到1万元）？
【答案】(1)，；
(2)当产品投入3.75万元，产品投入6.25万元，企业获得最大利润约为4万元．
【分析】（1）由已知给出的函数模型设出解析式，代入已知数据即可算出结果；
（2）设产品投入万元，则产品投入万元，设企业的利润为万元，则有，再利用换元法转化为求二次函数在给定区间上的最值问题即可求解．
【详解】（1）设投资额为万元，产品的利润为万元，产品的利润为万元，
由题设，，
由图可知（1），所以，又（4），所以，
所以，；
（2）设产品投入万元，则产品投入万元，设企业的利润为万元，
，，
令，则，，
所以当时，，此时，
所以当产品投入3.75万元，产品投入6.25万元，企业获得最大利润为万元，约为4万元．
25．（2023·江西鹰潭·二模）某公司为了对某种商品进行合理定价，需了解该商品的月销售量（单位：万件）与月销售单价（单位：元/件）之间的关系，对近6个月的月销售量和月销售单价数据进行了统计分析，得到一组检测数据如表所示：
月销售单价（单位：元/件）
4
5
6
7
8
9
月销售量（万件）
89
83
82
79
74
67
(1)若用线性回归模型拟合与之间的关系，现有甲、乙、丙三位实习员工求得回归直线方程分别为：，和，其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识，判断哪位实习员工的计算结果是正确的，并说明理由；
(2)已知该商品的月销售额为（单位：万元），利用（1）中的计算正确的结果回答问题：当月销售单价为何值时，啇品的月销值额预报值最大，并求出其最大值.
【答案】(1)甲，理由见解析
(2)时，商品的月销售额预报值最大，最大值为万元
【分析】（1）首先由数据可得，负相关，排除乙，再计算样本中心点，代入方程检验即可；
（2）由题意知，根据二次函数的性质计算可得.
【详解】（1）根据数据知，负相关，故排除乙，
又，，
由，可得过点，
由，可得不过点，
所以甲满足，丙不满足，故甲计算正确.
（2）根据题意
，
当时有最大值，
故当时，商品的月销售额预报值最大，最大值为万元.
26．（2023秋·重庆万州·高三重庆市万州第二高级中学校考期末）新型冠状病毒感染的肺炎治疗过程中，需要某医药公司生产的某种药品．该公司每年产生此药品不超过300千件，此药品的年固定成本为250万元，每生产x千件需另投入成本为（万元）．每千件药品售价为50万元，在疫情期间，该公司生产的药品能全部售完．
（Ⅰ）当年产量为多少千件时，在这一药品的生产中所获利润最大？利润最大是多少？
（Ⅱ）当年产量为多少千件时，每千件药品的平均利润最大？并求最大平均利润．
【答案】（Ⅰ）当年产量为200千件时，所获利润最大为3750万元；（Ⅱ）当年产量为50千件时，每千件药品的平均利润最大为30万元．
【解析】（Ⅰ）根据题意可得利润，根据二次函数性质即可求出最大值；
（Ⅱ）利用基本不等式可求出最大值.
【详解】（Ⅰ）设所获利润为万元，
则由题可得（），
当时，，
所以当年产量为200千件时，在这一药品的生产中所获利润最大为3750万元；
（Ⅱ）可知平均利润为，
当且仅当，即时等号成立，
所以当年产量为50千件时，每千件药品的平均利润最大为30万元．
考点六 利用分段函数模型解决实际问题
27．（2023·全国·高三专题练习）党的二十大报告将“完成脱贫攻坚､全面建成小康社会的历史任务，实现第一个百年奋斗目标”作为十年来对党和人民事业具有重大现实意义和深远历史意义的三件大事之一.某企业积极响应国家的号召，对某经济欠发达地区实施帮扶，投资生产A产品，经过市场调研，生产A产品的固定成本为200万元，每生产万件，需可变成本万元，当产量不足50万件时，；当产量不小于50万件时，.每件A产品的售价为100元，通过市场分析，生产的A产品可以全部销售完，则生产该产品能获得的最大利润为__________万元.
【答案】1000
【分析】依题意求得利润，借助导数和基本不等式可求得最大值.
【详解】由题意得，销售收入为万元，
当产量不足50万件时，利润；
当产量不小于50万件时，利润.
所以利润
因为当时，，
当时，单调递增；
当时，单调递减；
所以在上单调递增，在上单调递减，
则；
当时，，当且仅当时取等号.
又，故当时，所获利润最大，最大值为1000万元.
故答案为：1000
28．（2023·全国·高三专题练习）某公司生产一种电子仪器的固定成本为20000元，每生产一台仪器需增加投入100元，已知总收益满足函数，其中x是仪器的月产量．
(1)将利润表示为月产量的函数；
(2)当月产量为何值时，公司所获利润最大？最大利润为多少元？（总收益=总成本+利润）
【答案】(1)
(2)当月产量为时, 最大利润为元.
【分析】（1）利用利润=总收益固定成本投入成本，即可求解利润关于月产量x的函数；
（2）分段求解利润关于月产量的最大值并比较即可.
【详解】（1）
当时，，
当时，，
；
（2）当时，
当时，；
当时，在定义域内单调递减，
，

当时，；
当月产量为台时，公司所获利润最大，最大利润为元.
29．（2023·全国·高三专题练习）某乡镇响应“绿水青山就是金山银山”的号召，因地制宜的将该镇打造成“生态水果特色小镇”.经调研发现：某珍稀水果树的单株产量W（单位：千克）与施用肥料（单位：千克）满足如下关系：肥料成本投入为元，其它成本投入（如培育管理、施肥等人工费）元.已知这种水果的市场售价大约为15元/千克，且销路畅通供不应求.记该水果树的单株利润为（单位：元）.
(1)求的函数关系式；
(2)当施用肥料为多少千克时，该水果树的单株利润最大？最大利润是多少？
【答案】(1)
(2)当施用肥料为4千克时，该水果树的单株利润最大，最大利润为480元
【分析】（1）利用，即可求解；
（2）对进行化简，得到，然后，分类讨论和时，的取值，进而得到答案.
【详解】（1）根据题意，，化简得，

（2）由（1）得

当时，
当时，
当且仅当时，即时等号成立.
因为，所以当时，.
故当施用肥料为4千克时，该水果树的单株利润最大，最大利润为480元.
30．（2023·全国·高三专题练习）第24届冬季奥林匹克运动会，又称2023年北京冬季奥运会，是由中国举办的国际性奥林匹克赛事，于2023年2月4日开幕，2月20日闭幕.本届奥运会共设7个大项，15个分项，109个小项.北京赛区承办所有的冰上项目和自由式滑雪大跳台，延庆赛区承办雪车､雪橇及高山滑雪项目，张家口赛区承办除雪车､雪橇､高山滑雪和自由式滑雪大跳台之外的所有雪上项目，冬奥会的举办可以带动了我国3亿人次的冰雪产业，这为冰雪设备生产企业带来了新的发展机遇，某冰雪装备器材生产企业，生产某种产品的年固定成本为2000万元，每生产x千件，需另投入成本（万元）.经计算若年产量x千件低于100千件，则这x千件产品成本；若年产量x千件不低于100千件时，则这x千件产品成本.每千件产品售价为100万元，为了简化运算我们假设该企业生产的产品能全部售完.
(1)写出年利润（万元）关于年产量（千件）的函数解析式；
(2)当年产量为多少千件时，企业所获得利润最大？最大利润是多少？
【答案】(1)
(2)当该企业年产量为105千件时，所获得利润最大，最大利润是1000万元
【分析】（1）年利润为销售收入减去生产成本，分情况讨论计算即可；（2）当时，根据二次函数单调性求最大值；当时，根据基本不等式求最大值，继而求出最大值.
【详解】（1）当时，；
当时，.
所以
（2）当时，.
当时，取得最大值，且最大值为950.
当时，当且仅当时，等号成立.
因为，所以当该企业年产量为105千件时，所获得利润最大，最大利润是1000万元.
31．（2023·全国·高三专题练习）2023年11月5日至10日，第三届中国国际进口博览会在上海举行，经过三年发展，进博会让展品变商品，让展商变投资商，交流创意和理念，联通中国和世界，国际采购、投资促进、人文交流，开放合作四大平台作用不断凸显，成为全球共享的国际公共产品.在消费品展区，某企业带来了一款新型节能环保产品参展，并决定大量投放市场.已知该产品年固定研发成本为150万元，每生产1万台需另投入380万元.设该企业一年内生产该产品万台且全部售完，每万台的销售收入为万元，且.
(1)写出年利润（万元）关于年产量（万台）的函数解析式；（利润 = 销售收入—成本）
(2)当年产量为多少万台时，该企业获得的年利润最大？并求出最大年利润.
【答案】(1)
(2)当年产量为25万台时，该企业获得的年利润最大，最大为1490万元
【分析】（1）分和两种情况，由利润 = 销售收入—成本，知，再代入的解析式，进行化简整理即可，
（2）当时，利用配方法求出的最大值，当时，利用基本不等式求出的最大值，比较两个最大值后，取较大的即可
【详解】（1）当时，

，
当时，

，
所以年利润（万元）关于年产量（万台）的函数解析式为

（2）当时，，
所以函数在上单调递增，所以当时， 取得最大值1450，
当时，
，
当且仅当，即时取等号，此时取得最大值1490，
因为，
所以当年产量为25万台时，该企业获得的年利润最大，最大为1490万元
32．（2023·全国·高三专题练习）某乡镇响应“绿水青山就是金山银山”的号召，因地制宜的将该镇打造成“生态水果特色小镇”．经调研发现：某珍惜水果树的单株产量(单位：千克)与施用肥料(单位：千克)满足如下关系：，肥料成本投入为元，其它成本投入(如培育管理、施肥等人工费)元．已知这种水果的市场售价大约15元/千克，且销售畅通供不应求，记该水果单株利润为(单位：元)
(1)写单株利润(元)关于施用肥料(千克)的关系式；
(2)当施用肥料为多少千克时，该水果单株利润最大？最大利润是多少？
【答案】(1)；
(2)4千克，480元﹒
【分析】（1）用销售额减去成本投入得出利润的解析式；
（2）根据二次函数的单调性和基本不等式求出的最大值即可．
【详解】（1）依题意，又，
∴．
（2）当时，，开口向上，对称轴为，
在上单调递减，在上单调递增，
在上的最大值为．
当时，，
当且仅当时，即时等号成立．
∵，∴当时，．
∴当投入的肥料费用为40元时，种植该果树获得的最大利润是480元．
考点七 利用分式函数模型解决实际问题
33．（2023·全国·高三对口高考）某工厂统计资料显示,一种产品的次品率p与日产量x（件）（且）之间的关系如下表:
日产量x
1
2
3
4
5
…
98
99
100
次品率p





…



已知生产一件正品盈利a元,生产一件次品损失元．
(1)将该厂的日赢利额y（元）表示为日产量x（件）的函数;
(2)为使日赢利最大,该厂的日产量应定为多少？
【答案】(1),（,）
(2)96
【分析】(1)根据表格得到次品率p与日产量x之间的关系,再写出关于日赢利额y和日产量x的函数即可;
(2)根据(1)中的结论，对进行换元,分离常数,用基本不等式求出最值,以及取等条件即可.
【详解】（1）解:由表可知次品率(,）,
故
（,）．
（2）由(1)可得: ,（,）
设,则,,
可得


,
当且仅当,即时等号成立,
由,得,
所以日产量定为96件时可使日赢利最大．
34．（2023·上海·高三专题练习）某便民超市经销一种小袋装地方特色桃酥食品，每袋桃酥的成本为6元，预计当一袋桃酥的售价为元时，一年的销售量为万袋，并且全年该桃酥食品共需支付万元的管理费. 一年的利润一年的销售量售价（一年销售桃酥的成本一年的管理费）.（单位：万元）
(1)求该超市一年的利润（万元）与每袋桃酥食品的售价的函数关系式；
(2)当每袋桃酥的售价为多少元时，该超市一年的利润最大，并求出的最大值.
【答案】(1)；
(2)售价为9元时，利润最大为9万元
【分析】（1）直接由题目所给关系即可求得利润（万元）与售价的函数关系式；
（2）将函数关系式变形整理得，结合基本不等式即可求出最大值.
【详解】（1）由题意知，分公司一年的利润L（万元）与售价x的函数关系式为；
（2），因为，所以，
当且仅当即时取等号，此时最大为9万元.当每件产品的售价为9元时，该分公司一年的利润最大，且最大利润9万元.
35．（2023·全国·高三专题练习）首届世界低碳经济大会在南昌召开，本届大会以“节能减排，绿色生态”为主题.某单位在国家科研部门的支持下进行技术攻关，采取了新工艺，把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨，最多为600吨，月处理成本 (元)与月处理量 (吨)之间的函数关系可近似的表示为 ，且处理每吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时，才能使每吨的平均处理成本最低？
(2)该单位每月能否获利？如果获利，求出最大利润；如果不获利，则需要国家至少补贴多少元才能使单位不亏损？
【答案】(1)400吨；
(2)不获利，需要国家每个月至少补贴40000元才能不亏损.
【分析】（1）由题设平均每吨二氧化碳的处理成本为，应用基本不等式求其最小值，注意等号成立条件.
（2）根据获利，结合二次函数的性质判断是否获利，由其值域确定最少的补贴额度.
【详解】（1）由题意知，平均每吨二氧化碳的处理成本为；
当且仅当 ，即 时等号成立，
故该当每月处理量为400吨时，才能使每吨的平均处理成本最低为200元.
（2）不获利，设该单位每个月获利为S元，则 ，
因为，则，
故该当单位每月不获利，需要国家每个月至少补贴40000元才能不亏损.
36．（2023春·云南曲靖·高三宣威市第三中学校考阶段练习）2023 年初至今，新冠肺炎疫情袭击全球，对人民生命安全和生产生活造成严重影响. 在党和政府强有力的抗疫领导下，我国控制住疫情后，一方面防止境外疫情输入，另一方面逐步复工复产，减轻经济下降对企业和民众带来的损失. 为降低疫情影响，某厂家拟在2023年举行某产品的促销活动，经调查测算，该产品的年销售量(即该厂的年产量) x万件与年促销费用m万元(m≥0)满足 x= 4−. 已知生产该产品的固定成本为 8万元，生产成本为16万元 / 万件，厂家将产品的销售价格定为万元 / 万件 (产品年平均成本)的1.5倍.
(1)将2023年该产品的利润y万元表示为年促销费用m万元的函数；
(2)该厂家2023年的促销费用投入多少万元时，厂家的利润最大？
【答案】(1)
(2)3万元
【分析】（1）依据题意列出该产品的利润y万元关于年促销费用m万元的解析式即可；
（2）依据均值定理即可求得促销费用投入3万元时，厂家的利润最大.
【详解】（1）由题意知，每万件产品的销售价格为（万元），x= 4−
则2023年的利润．
（2）∵当时，，
∴，（当且仅当时等号成立）
∴，当且仅当万元时，（万元）．
故该厂家2023年的促销费用投入3万元时，厂家的利润最大为29万元．
37．（2023·全国·高三专题练习）如图所示，设矩形的周长为cm，把沿折叠，折过去后交于点，设cm，cm．

(1)建立变量与之间的函数关系式，并写出函数的定义域;
(2)求的最大面积以及此时的的值．
【答案】(1)，定义域为
(2)，的最大面积为
【分析】（1）由题意可得，再由可求出的取值范围，
（2）设，在直角三角形ADP中利用勾股定理可得，从而可求得，化简后利用基本不等式可求得结果
【详解】（1）因为，，矩形ABCD的周长为20cm，
所以，因为，所以，
解得．所以，定义域为．
（2）因为ABCD是矩形，所以有，．
因为是沿折起所得，
所以有，，因此有，
，所以≌，因此，．
设．而ABCD是矩形，所以，
因此．
在直角三角形ADP中，有，．
所以，
化简得，
当且仅当时取等号，即时，的最大面积为．
考点八 利用指数函数模型解决实际问题
38．（2023·甘肃武威·统考三模）2023年8月，中科院院士陈发虎带领他的团队开始了第二次青藏高原综合科学考察．在科考期间，陈院士为同行的科研人员讲解专业知识，在空气稀薄的高原上开设了“院士课堂”．已知某地大气压强与海平面大气压强之比为b，b与该地海拔高度（单位：米）满足关系：（k为常数，e为自然对数的底）． 若科考队算得A地，海拔8700米的B地 ，则A，B两地的高度差的绝对值约为（，）（    ）
A．3164米 B．4350米 C．5536米 D．6722米
【答案】A
【分析】设地海拔高度为，由题意可得，，解方程可得，进而求解.
【详解】设地海拔高度为，
由已知可得，，
则，，
所以，
所以（米）.
故选：A.
39．（2023届福建省福州市高三质量检测数学试题）为落实党的二十大提出的“加快建设农业强国，扎实推动乡村振兴”的目标，银行拟在乡村开展小额贷款业务.根据调查的数据，建立了实际还款比例关于贷款人的年收入（单位：万元）的Logistic，模型：，已知当贷款大的年收入为8万元时，其实际还款比例为50%.若银行希望实际还款比例为40%，则贷款人的年收入为（    ）（精确到0.01万元，参考数据：，）
A．4.65万元 B．5.63万元 C．6.40万元 D．10.00万元
【答案】A
【分析】先根据题中数据代入计算函数中参数的值，然后计算时的值即可.
【详解】由题意，即，得，所以.
令，
得，
得，
得
得.
故选：A.
40．（2023春·江西赣州·高三校联考期中）赣南脐橙，江西省赣州市特产，中国国家地理标志产品.赣南脐橙年产量达百万吨，原产地江西省赣州市已经成为脐橙种植面积世界第一，年产量世界第三，全国最大的脐橙主产区.假设某赣南脐橙种植区的脐橙产量平均每年比上一年增长，若要求该种植区的脐橙产量高于当前脐橙产量的6倍，则至少需要经过的年数为（    ）（参考数据：取）
A．9 B．10 C．11 D．12
【答案】B
【分析】先根据条件建立对数不等式，从而得到，再利用换底公式即可求出的值，进而求出的范围得到结果.
【详解】假设当前该种植区的脐橙产量为1，经过年该种植区的脐橙产量为，
由题意得，得到，
又因为，
所以，故至少需要经过的年数为10.
故选：B.
41．（2023春·云南玉溪·高三云南省玉溪第一中学校考阶段练习）酒驾是严重危害交通安全的违法行为.根据国家有关规定：驾驶人血液中的酒精含量大于（或等于）毫克/毫升，小于毫克/毫升的情况下驾驶机动车属于饮酒驾车；含量大于（或等于）毫克/毫升的情况下驾驶机动车属于醉酒驾车.假设某驾驶员一天晚上点钟喝了一定量的酒后，其血液中酒精含量上升到了毫克/毫升.如果在停止喝酒后，他血液中酒精含量以每小时的速度减少，那么他次日上午最早几点（结果取整数）开车才不构成酒驾？（参考数据：，）（    ）
A．8点 B．9点 C．10点 D．11点
【答案】C
【分析】假设经过小时后，驾驶员开车才不构成酒驾，则，由对数的运算性质解不等式即可得出答案.
【详解】假设经过小时后，驾驶员开车才不构成酒驾，
则，即，，
则，
，次日上午最早点，该驾驶员开车才不构成酒驾.
故选：C.
42．（2023·贵州·统考模拟预测）某工厂产生的废气经过过滤后排放，已知在过滤过程中的污染物的残留含量（单位：）与过滤时间（单位：）之间的函数关系为，其中是自然对数的底数，为常数，为原污染物总量.若前5个小时废气中的污染物被过滤掉了，则污染物被过滤掉了所需时间约为（    ）
A． B． C． D．
【答案】C
【分析】根据题意列出方程，求出，得到函数解析式，再设出未知数，解方程，求出答案.
【详解】由题意得，化简得，
两边取对数，，故，
故
设污染物被过滤掉了所需时间约为，
则，化简得，
即，解得，
故污染物被过滤掉了所需时间约为77h.
故选：C
考点九 利用对数函数模型解决实际问题
43．（2023·全国·高三专题练习）某地为了抑制一种有害昆虫的繁殖，引入了一种以该昆虫为食物的特殊动物，已知该动物的繁殖数量（只）与引入时间（年）的关系为，若该动物在引入一年后的数量为180只，则15年后它们发展到（    ）
A．300只 B．400只 C．600只 D．720只
【答案】D
【分析】根据题意求得，当时即可求解.
【详解】由题知，该动物的繁殖数量（只）与引入时间（年）的关系为，
当代入得，，得，
所以，
所以当时，，
所以15年后它们发展到720只.
故选：D
44．（2023春·山西·高三校联考阶段练习）净水机通过分级过滤的方式使自来水逐步达到纯净水的标准，其中的核心零件是多层式结构的棉滤芯（聚丙烯熔喷滤芯），主要用于去除铁锈､泥沙､悬浮物等各种大颗粒杂质.假设每一层棉滤芯可以过滤掉的大颗粒杂质，过滤前水中大颗粒杂质含量为，若要满足过滤后水中大颗粒杂质含量不超过，则棉滤芯层数最少为（    ）（参考数据：，）
A． B． C． D．
【答案】C
【分析】根据指数与对数的运算直接求解.
【详解】由题意得，经层滤芯过滤后水中大颗粒杂质含量为，，
则，得，所以，
即，所以，
解得，，
所以的最小值为，
故选：C.
45．（2023·贵州黔东南·凯里一中校考三模）酒驾是严重危害交通安全的违法行为．为了保障交通安全，根据国家有关规定：100mL血液中酒精含量达到20~79mg的驾驶员即为酒后驾车，80mg及以上认定为醉酒驾车．假设某驾驶员喝了一定量酒后，其血液中的酒精含量上升到了1mg/mL．如果在停止喝酒以后，他血液中酒精含量会以每小时20%的速度减少，那他至少经过（    ）小时才能驾驶．（参考数据）
A．5 B．6 C．7 D．8
【答案】D
【分析】由题意可得，由对数的运算性质求解即可.
【详解】解析：设该驾驶员x小时后100mL血液中酒精含量为ymg，
则，
当时，有，即，
∴，
故选：D．
46．（2023秋·内蒙古阿拉善盟·高三阿拉善盟第一中学校考期末）某地锰矿石原有储量为a万吨，计划每年的开采量为本年年初储量的m（，且m为常数）倍，第n（）年开采后剩余储量为，按该计划使用10年时间开采到剩余储量为原有储量的一半.若开采到剩余储量为原有储量的70%，则需开采约（参考数据：）（    ）
A．3年 B．4年 C．5年 D．6年
【答案】C
【分析】设第n年开采后剩余储量为y，则，计算，得到，解得答案.
【详解】设第n年开采后剩余储量为y，则，
当时，，所以，，故，即，
，设第n年时，，
故，，，故.
故选：C
47．（2023·江苏·高三统考学业考试）2023年2月6日，土耳其发生强烈地震，造成重大人员伤亡和财产损失，江苏救援队伍紧急赴当地开展救报行动.尽管日前人类还无法准确预报地震，但科学家通过研究，已经对地震有所了解，例如，地震时释放的能量E（单位：焦耳）与地震里氏震级M之间的关系为.里氏8.0级地震所释放出来的能量是里氏6.0级地震所释放出来的能量的（    ）
A．6倍 B．倍 C．倍 D．倍
【答案】C
【分析】代入数据计算，，计算得到答案.
【详解】，；，，
.
故选：C
48．（2023·北京·高三专题练习）在不考虑空气阻力的条件下，火箭的最大速度和燃料的质量以及火箭（除燃料外）的质量间的关系为．若火箭的最大速度为，则下列各数中与最接近的是（    ）（参考数据：）
A． B．
C． D．
【答案】B
【分析】根据所给关系式，求出，近似计算得解.
【详解】由题意，火箭的最大速度为时，可得，
即，
因为，所以近似计算可得，
故选：B
考点十 利用幂函数模型解决实际问题

49．（2023·全国·高三专题练习）某公司的收入由保险业务收入和理财业务收入两部分组成.该公司年总收入为亿元，其中保险业务收入为亿元，理财业务收入为亿元.该公司经营状态良好、收入稳定，预计每年总收入比前一年增加亿元.因越来越多的人开始注重理财，公司理财业务发展迅速.要求从年起每年通过理财业务的收入是前一年的倍，若要使得该公司年的保险业务收入不高于当年总收入的，则的值至少为（    ）
A． B． C． D．
【答案】A
【分析】求出年通过理财业务的收入为亿元，根据题意可得出关于的不等式，解出的范围即可得解.
【详解】因为该公司年总收入为亿元，预计每年总收入比前一年增加 亿元，所以年的总收入为亿元，
因为要求从年起每年通过理财业务的收入是前一年的倍，
所以年通过理财业务的收入为亿元，所以，解得.故的值至少为，
故选：A.
50．（2023·全国·高三专题练习）2023年底，国务院扶贫办确定的贫困县全部脱贫摘帽，脱贫攻坚取得重大胜利！为进一步巩固脱贫攻坚成果，持续实施乡村振兴战略，某企业响应政府号召，积极参与帮扶活动．该企业2023年初有资金150万元，资金的年平均增长率固定，每三年政府将补贴10万元．若要实现2024年初的资金达到270万元的目标，资金的年平均增长率应为（参考值：）（    ）
A．10% B．20% C．22% D．32%
【答案】B
【分析】设年平均增长率为，依题意列方程求即可.
【详解】由题意，设年平均增长率为，则，
所以，故年平均增长率为20%.
故选：B
51．（2023·全国·高三专题练习）异速生长规律描述生物的体重与其它生理属性之间的非线性数量关系通常以幂函数形式表示．比如，某类动物的新陈代谢率与其体重满足，其中和为正常数，该类动物某一个体在生长发育过程中，其体重增长到初始状态的16倍时，其新陈代谢率仅提高到初始状态的8倍，则为（    ）
A． B． C． D．
【答案】D
【分析】初始状态设为，变化后为，根据，的关系代入后可求解．
【详解】设初始状态为，则，，
又，，即，
，，，，．
故选：D．