

2021-2023年浙江省高考物理模拟试题分类——专题7机械能守恒定律 计算题
展开
这是一份2021-2023年浙江省高考物理模拟试题分类——专题7机械能守恒定律 计算题,共50页。试卷主要包含了,求铅球,和与J相切的水平直轨道JK组成等内容,欢迎下载使用。
2021-2023年浙江省高考物理模拟试题分类——专题7机械能守恒定律 计算题
一.试题(共22小题)
1.(2022•温州二模)我国选手谷爱凌在北京冬奥会自由式滑雪好U形场地技巧决赛中夺得金牌。如图所示,某比赛用U形池场地长度L=160m、宽度d=20m、深度h=7.25m,两边竖直雪道与池底平面雪道通过圆弧雪道连接组成,横截面像“U”字形状,池底雪道平面与水平面夹角为θ=20°。为测试赛道,将一质量m=1kg的小滑块从U形池的顶端A点以初速度v0=0.7m/s滑入;滑块从B点第一次冲去U形池,冲出B点的速度vB=10m/s,与竖直方向夹角为α (α未知),再从C点重新落回U形池(C点图中未画出)。已知A、B两点间直线距离为25m,不计滑块所受的空气阻力,sin20°=0.34,cos20°=0.94,tan20°=0.36。
(1)A点至B点过程中,求小滑块克服雪道阻力所做的功Wf;
(2)忽略雪道对滑块的阻力,若滑块从池底平面雪道离开,求滑块离开时速度v的大小;
(3)若保持vB大小不变,调整速度vB与竖直方向的夹角为α0时,滑块从冲出B点至重新落回U形池的时间最长,求tanα0。
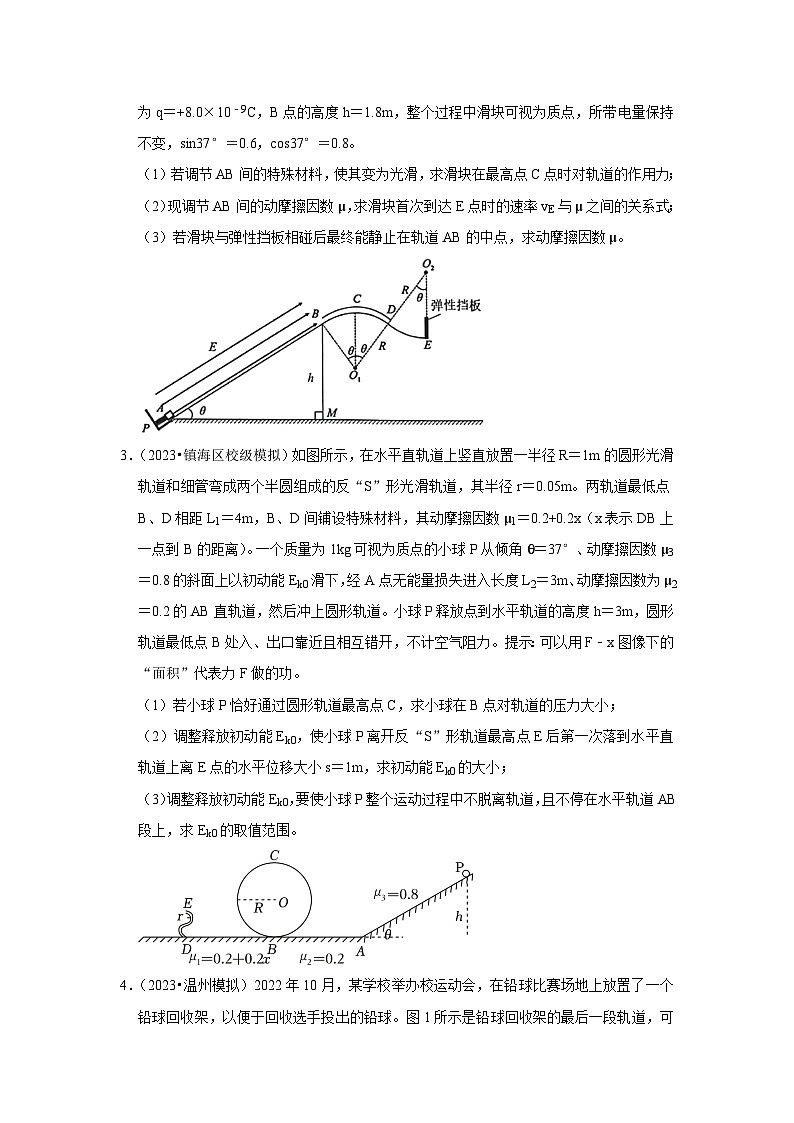
2.(2022•宁波二模)如图所示,在竖直平面内,某一游戏轨道由直轨道AB、光滑圆弧细管道BCD和光滑圆弧轨道DE平滑连接组成,两段圆弧半径相等R=0.5m,B、D等高,图中θ角均为37°,AB与圆弧相切,AM水平。直轨道AB上方有与AB相平行的匀强电场E=108N/C,且电场只分布在AB之间。直轨道AB底端装有弹射系统(弹簧长度很短,长度和质量不计,可以认为滑块从A点射出),具有初始弹性势能EP=2.5J,某次弹射系统将尺寸略小于管道内径的带正电的滑块弹出,冲上直轨道AB,直轨道AB上铺有特殊材料,使滑块与轨道AB间的动摩擦因数μ大小可调。滑块进入光滑圆轨道后,最后能在E点与弹性挡板相互作用后以等速率弹回。已知滑块的质量为m=0.1kg,带电量为q=+8.0×10﹣9C,B点的高度h=1.8m,整个过程中滑块可视为质点,所带电量保持不变,sin37°=0.6,cos37°=0.8。
(1)若调节AB间的特殊材料,使其变为光滑,求滑块在最高点C点时对轨道的作用力;
(2)现调节AB间的动摩擦因数μ,求滑块首次到达E点时的速率vE与μ之间的关系式;
(3)若滑块与弹性挡板相碰后最终能静止在轨道AB的中点,求动摩擦因数μ。
3.(2023•镇海区校级模拟)如图所示,在水平直轨道上竖直放置一半径R=1m的圆形光滑轨道和细管弯成两个半圆组成的反“S”形光滑轨道,其半径r=0.05m。两轨道最低点B、D相距L1=4m,B、D间铺设特殊材料,其动摩擦因数μ1=0.2+0.2x(x表示DB上一点到B的距离)。一个质量为1kg可视为质点的小球P从倾角θ=37°、动摩擦因数μ3=0.8的斜面上以初动能Ek0滑下,经A点无能量损失进入长度L2=3m、动摩擦因数为μ2=0.2的AB直轨道,然后冲上圆形轨道。小球P释放点到水平轨道的高度h=3m,圆形轨道最低点B处入、出口靠近且相互错开,不计空气阻力。提示:可以用F﹣x图像下的“面积”代表力F做的功。
(1)若小球P恰好通过圆形轨道最高点C,求小球在B点对轨道的压力大小;
(2)调整释放初动能Ek0,使小球P离开反“S”形轨道最高点E后第一次落到水平直轨道上离E点的水平位移大小s=1m,求初动能Ek0的大小;
(3)调整释放初动能Ek0,要使小球P整个运动过程中不脱离轨道,且不停在水平轨道AB段上,求Ek0的取值范围。
4.(2023•温州模拟)2022年10月,某学校举办校运动会,在铅球比赛场地上放置了一个铅球回收架,以便于回收选手投出的铅球。图1所示是铅球回收架的最后一段轨道,可简化为如图2所示的ABCDE轨道,其中AB、BC、CD轨道均为直轨道且平滑连接,长度分别为LAB=1.0m、LBC=1.6m、LCD=0.6m,与水平方向的夹角分别为θ1=37°、θ2=15°、θ3=37°。一质量m=4kg的铅球,从A点以某一速度冲上AB轨道,运动到B点时速度恰好为0,然后经过BC轨道冲上CD轨道。若铅球在AB、CD轨道运动时所受的轨道阻力恒为Ff1=8N,在BC轨道运动时所受的轨道阻力恒为Ff2=9.6N,不计其它阻力,铅球大小可忽略。(取sin37°=0.6,cos37°=0.8,sin15°=0.26,cos15°=0.96),求铅球
(1)冲上AB轨道时的初速度大小vA;
(2)运动到轨道C点时的速度大小vc;
(3)从轨道A点到在CD轨道上速度第一次减为零时所用的总时间t总。
5.(2023•浙江模拟)某闯关项目的简化图如图所示,距离水平地面高为h=1.8m的平台上,A点左侧为光滑平台,一根弹簧左端与固定挡板连接,自然长度时右端不超过A点,一个可以看作质点的滑块靠着弹簧右端(不拴连),滑块质量为m=1kg。平台AB段长为L1=2.0m,与滑块的动摩擦因数为μ1=0.1。B点右侧设置长为L2=1.5m的水平传送带,传送带与滑块的动摩擦因数为μ2,传送带的右端设置半径为R=0.9m的半圆弧光滑轨道,CD为竖直直径的上下两端,C点与传送带末端的空隙很小,但是可以让滑块通过。传送带一且启动,顺转(即让传送带顺时针方向转动)和逆转的速度都为v=4m/s,在B点的左侧附近设置传送带启动按钮,按钮有两个,一个为顺转,一个为逆转。闯关开始前传送带处于关闭状态。闯关时,选手首先向左推滑块压缩弹簧,使弹簧具有一定的初始弹性势能EP,然后释放滑块,在滑块进入传送带前,选手必须按照实时情况按下顺转按钮或逆转按钮。闯关规则为:如果滑块最终能始终沿着轨道到达水平地面,则闯关成功;如果滑块最终退回到A点左侧,则可以再次闯关(既不失败,也没有成功);如果滑块最终停在AB段上,或者向右出传送带后摔落在CD段则游戏失败(来不及按下按钮也视为失败,本题假设选手都按了按钮)。g取10m/s2。
(1)设备调试时,关闭传送带,测得当弹簧的初始弹性势能为EP=5.0J时,滑块恰好滑到传送带的右端停止,求传送带与滑块的动摩擦因数μ2的大小;
(2)某选手压缩弹簧使其具有EP=4.5J的初始弹性势能,请通过计算说明本次闯关选手(按下任何一个按钮的可能性都会有)是否可能会失败;
(3)求选手按下任意一个按钮都能闯关成功的初始弹簧弹性势能EP取值范围。
6.(2022•宁波模拟)如图所示,一游戏装置由安装在水平台面上的高度h可调的斜轨道AB、竖直圆轨道(在最低点E分别与水平轨道AE和EG相连)、细圆管道GHIJ(HI和IJ为两段四分之一圆弧)和与J相切的水平直轨道JK组成。可认为所有轨道均处在同一竖直平面内,连接处均平滑。已知,滑块质量为m=30g且可视为质点,竖直圆轨道半径为r=0.45m小圆弧管道HI和大圆弧管道IJ的半径之比为1:4,L1=1.5m不变,L2=0.5m,滑块与AB、EG及JK间摩擦因数均为μ=0.5,其他轨道均光滑,不计空气阻力,忽略管道内外半径差异。现调节h=2m,滑块从B点由静止释放后,贴着轨道恰好能滑上水平直轨道JK,求:
(1)大圆弧管道IJ的半径R;
(2)滑块经过竖直圆轨道与圆心O等高的P点时对轨道的压力F1与运动到圆弧管道最低点H时对轨道的压力F2大小之比;
(3)若在水平轨道JK上某一位置固定一弹性挡板,当滑块与之发生弹性碰撞后能以原速率返回,若第一次返回时滑块不脱轨就算游戏闯关成功。调节斜轨道的高度为h=3m,仍让滑块从B点由静止滑下,问弹性挡板与J的间距L满足什么条件时游戏能闯关成功。
7.(2021•瓯海区校级模拟)如图所示,在高h1=30m的水平平台上有一质量m=1kg的小物块(可视为质点),它在F=20N的水平外力作用下从离平台右端l=5m处由静止开始向右做直线运动,物块与平台间的动摩擦因数μ0=0.2,作用一段距离x后撤去力F,物块又滑行一段距离后从平台右端水平抛出,物块抛出后,恰好能从光滑圆弧形轨道BC的B点沿切线方向进入圆弧形轨道。B点的高度h2=15m,圆弧轨道的圆心O与平台等高,轨道最低点C的切线水平,并与地面上长度L=70m的水平粗糙轨道CD平滑连接;小物块沿轨道BCD运动并与右边墙壁发生碰撞,取g=10m/s2。
(1)求水平外力F的作用的距离x;
(2)若小物块与墙壁只发生一次碰撞,碰后物块的速度等大反向、反向运动过程中物块没有冲出B点,最后停在轨道CD上的P点(P点没画出),设小物块与轨道CD之间的动摩擦因数为μ,求μ的取值范围。
8.(2023•嘉兴一模)如图所示,某游乐场游乐装置由竖直面内轨道BCDE组成,左侧为半径R=0.8m的光滑圆弧轨道BC,轨道上端点B和圆心O的连线与水平方向的夹角α,下端点C与粗糙水平轨道CD相切,DE为倾角θ=37°的粗糙倾斜轨道,一轻质弹簧上端固定在E点处的挡板上。现有质量为m=0.1kg的小滑块P(视为质点)从空中的A点以v0=22m/s的初速度水平向左抛出,经过65s后恰好从B点沿轨道切线方向进入轨道,沿着圆弧轨道运动到C点之后继续沿水平轨道CD滑动,经过D点后沿倾斜轨道向上运动至F点(图中未标出),弹簧恰好压缩至最短,已知CD=DF=1m,滑块与轨道CD、DE间的动摩擦因数为μ=0.1,各轨道均平滑连接,不计其余阻力,sin37°=0.6。求:
(1)BO连线与水平方向的夹角α的大小;
(2)小滑块P到达与O点等高的O'点时对轨道的压力;
(3)弹簧的弹性势能的最大值;
(4)试判断滑块返回时能否从B点离开,若能,求出飞出时对B点的压力大小;若不能,判断滑块最后位于何处。
9.(2023•浙江模拟)如图所示,半径R=2.45m的竖直光滑14圆弧轨道AB,其底端右侧是一个凹槽,凹槽右端连接一个半径r=0.40m的光滑圆轨道,轨道固定在竖直平面内,D与圆心连线与竖直方向成θ=37°角。一质量为m=1kg的滑板Q放置在凹槽内水平面上,其上表面刚好与B点和C点水平等高。开始时滑板静置在紧靠凹槽左端处,此时滑板右端与凹槽右端的距离d=0.60m。一质量也为m的小物块P(可视为质点)从A点由静止滑下,当物块滑至滑板右端时滑板恰好到达凹槽右端,撞击后滑板立即停止运动。已知物块与滑板间的动摩擦因数μ=0.75,其余接触面的摩擦均可忽略不计,取重力加速度g=10m/s2。
(1)求滑块滑至B点时对B点的压力;
(2)求滑板的长度l;
(3)请通过计算说明滑块滑上CD轨道后能否从D点飞出?
10.(2022•杭州二模)公交站点1与站点2之间的道路由水平路面AB段、CD段及倾角为15°的斜坡BC段组成,斜坡足够长。一辆公交车额定功率为210kW,载人后总质量为8000kg。该车在AB段以54km/h的速率匀速行驶,此过程该车的实际功率为额定功率的一半。该车到达C点时的速率为21.6km/h,此后在大小恒为1.4×104N的牵引力作用下运动,直到速度达到54km/h时关闭发动机自由滑行,结果该车正好停在了D点(站点2)。若在整个行驶过程中,公交车的实际功率不超过额定功率,它在每一个路段的运动都可看成直线运动,它受到的由地面、空气等产生的阻力F1大小不变。已知sin15°=0.26,求:
(1)F1的大小;
(2)公交车上坡过程中能够保持匀速行驶的最大速率;
(3)C点与D点之间的距离。
11.(2021•浙江模拟)有一弹射打板游戏装置,其结构如图所示,半径R=0.4m的竖直光滑圆弧轨道BC固定在水平底座CD上,轨道的上端点B和圆心O的连线与水平方向的夹角θ=30°,C、D两点间的距离L=1.2m;D点与弹射装置相连,弹射装置的弹性势能Ep=2.0J。装置的上方有一高h=0.4m可水平移动的竖直挡板,挡板的下端点A与BC轨道有一定间距。在某次游戏中,一质量m0=0.1kg的弹射物(可视为质点)从弹射器弹出,经DC沿圆弧轨道从B点抛出,恰好从A点贴近挡板水平飞出,已知弹射物与水平面间的动摩擦因数μ=0.5,不计空气阻力,g取10m/s2求:
(1)弹射物经过圆弧轨道上C点时对轨道的压力;
(2)弹射物经过圆弧轨道上B点时的速度vB的大小:
(3)挡板的下端点A与轨道最高点B的高度差:,
(4)现减小弹射物的质量,并且要求弹射物与挡板垂直相碰,试写出挡板水平距离×(A与B点的水平间距)与弹射物的质量m的函数关系。
12.(2022•浙江模拟)如图所示,质量均为m=4kg的两个小物块A、B(均可视为质点)放置在水平地面上,竖直平面内半径R=0.4m的光滑半圆形轨道与水平地面相切于C,弹簧左端固定。移动物块A压缩弹簧到某一位置(弹簧在弹性限度内),由静止释放物块A,物块A离开弹簧后与物块B碰撞并粘在一起以共同速度v=5m/s向右运动,运动过程中经过一段长为s,动摩擦因数μ=0.2的水平面后,冲上圆轨道,除s段外的其他水平面摩擦力不计。求:(g取10m/s2)
(1)若s=1m,两物块刚过C点时对轨道的压力大小;
(2)若两物块能冲上圆形轨道,且不脱离圆形轨道,s应满足什么条件。
13.(2021•岱山县校级模拟)如图所示,水平放置的轻质弹簧原长为2L,一端与质量m1=2kg的物块P接触但不连接,另一端固定在A点,光滑水平轨道AB长度为5L.长度为L0=2.5m的水平传送带分别与B端和水平光滑轨道CD平滑连接,物块P与传送带之间的动摩擦因数μ=0.2,传送带始终以v=2m/s的速率顺时针匀速转动.质量为m2=6kg小车放在光滑水平轨道上,位于CD右侧,小车左端与CD段平滑连接,小车的水平面长度L1=0.5m,右侧是一段半径R=0.5m的四分之一光滑圆弧,物块P与小车水平上表面的动摩擦因数μ1=0.1.用外力推动物块P,将弹簧压缩至长度L,然后放开,P开始沿轨道运动,冲上传送带后开始做减速运动,到达传送带右端时速度恰好与传送带速度大小相等.重力加速度大小g=10m/s2.求:
(1)弹簧压缩至长度L时储存的弹性势能Ep;
(2)物块P在小车圆弧上上升的最大高度H;
(3)要使物块P既可以冲上圆弧又不会从小车上掉下来,小车水平面长度的取值范围。
14.(2021•金华模拟)如图所示,竖直放置的半径为R=0.2m的螺旋圆形轨道BGEF与水平直轨道MB和BC平滑连接,倾角为θ=30°的斜面CD在C处与直轨道BC平滑连接。水平传送带MN以v0=4m/s的速度顺时针方向运动,传送带与水平地面的高度差为h=0.8m,MN间的距离为LMN=3.0m,小滑块P与传送带和BC段轨道间的摩擦因数μ=0.2,轨道其他部分均光滑。直轨道BC长LBC=1m,小滑块P质量为m=1kg。
(1)若滑块P第一次到达圆轨道圆心O等高的F点时,对轨道的压力刚好为零,求滑块P从斜面静止下滑处与BC轨道高度差H;
(2)若滑块P从斜面高度差H=1.0m处静止下滑,求滑块从N点平抛后到落地过程的水平位移;
(3)滑块P在运动过程中能二次经过圆轨道最高点E点,求滑块P从斜面静止下滑的高度差H范围。
15.(2022•浙江模拟)某游乐场的滑梯可以简化为如图所示竖直面内的ABCD轨道,AB为长L=6m、倾角α=37°的斜轨,BC为水平轨道,CD为半径R=15m、圆心角β=37°的圆弧,轨道AB段粗糙其余各段均光滑。一小孩(可视为质点)从A点以初速度v0=23m/s下滑,沿轨道运动到D点时的速度恰好为零(不计经过B点时的能量损失)。已知该小孩的质量m=30kg,取sin37°=0.6,cos37°=0.8,不计空气阻力,设最大静摩擦力等于滑动摩擦力。求:
(1)该小孩第一次经过圆弧C点时,对圆弧轨道的压力FN;
(2)该小孩在轨道AB上第一次从A下滑到B的时间t;
(3)若将AB段轨道改为圆弧形状(图中虚线部分,轨道材质不变),试定性说明题设条件下小孩在轨道上游玩时是否会冲出D点而发生危险?
16.(2022•绍兴二模)如图甲所示为北京首钢滑雪大跳台,模型简化如图乙所示,AB 和EF是长为L1=50m的倾斜滑到,倾角为θ=37°,CD是长为L2=30m 的水平滑道,倾斜滑道AB、EF和水平滑道CD之间分别用一圆弧轨道连接,圆弧轨道半径为R=10m,圆心角为θ=37°,FG为结束区。一质量为m=90kg的运动员从A点静止滑下沿滑道ABCD运动,从D点沿水平方向滑离轨道后,完成空翻、回转等技术动作,落到倾斜轨道,最后停在结束区。为简化运动,运动员可视为质点,不计空气阻力。
(1)运动员刚好从D点沿水平方向滑离轨道,求运动员在D点的速度;
(2)在(1)情形下,求从开始运动到完成表演落到倾斜轨道过程中摩擦阻力做的功;
(3)运动员可以在滑道ABCD滑行过程中利用滑雪杖支撑前进,获取一定的能量ΔE,要使运动员安全停留在结束区,落到倾斜轨道上的动能不能超过15250J,求ΔE大小应满足的条件。
17.(2021•浙江模拟)简谐运动是一种常见且重要的运动形式。它是质量为m的物体在受到形如F=﹣kx的回复力作用下,物体的位移x与时间t遵循x=Asinωt变化规律的运动,其中角频率ω=2πT=km(k为常数,A为振幅,T为周期)。弹簧振子的运动就是其典型代表。
如图所示,一竖直光滑的管内有一劲度系数为k的轻弹簧,弹簧下端固定于地面,上端与一质量为m的小球A相连,小球A静止时所在位置为O,另一质量也为m的小球B从距A为H的P点由静止开始下落,与A发生瞬间碰撞后一起开始向下做简谐运动。两球均可视为质点,在运动过程中,弹簧的形变在弹性限度内,当其形变量为x时,弹性势能为Ep=12kx2,已知H=3mgk,重力加速度为g。求:
(1)B与A碰撞后瞬间一起向下运动的速度;
(2)小球A被碰后向下运动离O点的最大距离。
(3)小球A从O点开始向下运动到第一次返回O点所用的时间。
18.(2021•宁波二模)如图所示是一弹射游戏装置,由安装在水平台面上的固定弹射器、竖直圆轨道(在最低点A、C分别与水平轨道OA和CD相连)、倾斜长轨道DE组成。游戏时滑块从O点弹出后,经过圆轨道并滑上倾斜长轨道DE,若滑块从长轨道DE滑下则反向进入圆轨道,从圆轨道滑出,进入AO轨道并压缩弹射器的弹簧,随后能再次弹出(无能量损失)算游戏成功。已知圆轨道半径为R,轨道DE的倾角θ=37°,滑块质量为m,滑块与轨道DE之间的动摩擦因数μ=0.5,其余都光滑,各轨道之间平滑连接;滑块可视为质点,弹射时从静止释放且弹簧的弹性势能完全转化为滑块动能,忽略空气阻力,sin37°=0.6,cos37°=0.8,重力加速度为g。
(1)若滑块第一次进入圆轨道,恰好能过最高点B,求滑块能滑上斜轨道的最大距离;
(2)若某次游戏弹射释放的弹性势能为Ep=5mgR,求滑块在斜轨道上通过的总路程;
(3)要使游戏成功(即滑块能返回弹射器、且只能返回一次),并要求滑块始终不脱离轨道,求弹射时弹性势能可能的范围。
19.(2023•杭州二模)如图所示,某游戏装置由光滑平台、轨道AB、竖直圆管道BCDEC(管道口径远小于管道半径)、水平轨道CF、光滑直轨道FG平滑连接组成,B、C、C′为切点,A、F连接处小圆弧长度不计,A点上方挡片可使小滑块无能量损失地进入轨道AB。圆管道半径R=0.2m,管道中,内侧粗糙,外侧光滑。小滑块与轨道AB、CF的动摩擦因数均为μ=0.5,AB轨道长度l=0.4m,倾角θ=37°,CF长度L=2m,FG高度差h=0.8m,平台左侧固定一轻质弹簧,第一次压缩弹簧后释放小滑块,恰好可以运动到与管道圆心等高的D点,第二次压缩弹簧使弹性势能为0.36J时释放小滑块,小滑块运动到圆管道最高处E的速度为vE=1m/s,已知小滑块质量m=0.1kg可视为质点,sin37°=0.6,cos37°=0.8,不计空气阻力。求;
(1)第一次释放小滑块,小滑块首次到圆管上的C点时受到弹力大小;
(2)第二次释放小滑块,小滑块从C点运动到E点的过程,圆管道对滑块的摩擦力做的功;
(3)若第三次压缩弹簧使弹性势能为Ep时释放小滑块,要求小滑块在圆管道内运动时不受到摩擦力且全程不脱轨,最终停在C′F上。写出小滑块C′F上运动的总路程s与Ep之间的关系式,并指出Ep的取值范围。
20.(2021•浙江二模)如图1是组合玩具实物图,该玩具主要配件有小车、弹射器、三连环、滑跃板及部分直线轨道等。如图2为该玩具的轨道结构示意图,其中三连环是三个半径不同圆轨道Ⅰ、Ⅱ、Ⅲ组成,且轨道连接但不重叠。其圆心分别为O1、O2、O3,半径分别为R1=20cm、R2=15cm、R3=10cm,OA、AC为光滑水平轨道,滑跃板CD为足够长的粗糙倾斜轨道,轨道与水平面夹角θ可调(0≤θ<90o)。某次游戏中弹射器将小车自O点以一定初速度弹出,小车先后通过圆轨道Ⅰ、Ⅱ、Ⅲ后冲上滑跃板。小车可视为质点,其质量m=0.1kg,与滑跃板CD间动摩擦因数μ=33,其它阻力均不计,轨道各部分平滑连接,g取10m/s2。
(1)求小车通过圆轨道Ⅰ最高点B的最小速度vB;
(2)改变弹射器对小车的冲量,小车均能通过三连环,求小车通过圆轨道Ⅲ最低点A时受到轨道的支持力与弹射器对小车冲量的关系;
(3)若小车恰好能够通过三连环,为确保小车整个运动过程均不脱离轨道,分析滑跃板CD与水平面间夹角θ的取值范围。(可用三角函数表示)
21.(2023•浙江模拟)如图为某游戏装置的示意图。AB、CD均为四分之一圆弧,E为圆弧DEG的最高点,各圆弧轨道与直轨道相接处均相切。GH与水平夹角为θ=37°,底端H有一弹簧,A、O1、O2、D、O3、H在同一水平直线上。一质量为0.01kg的小钢球(其直径稍小于圆管内径,可视作质点)从距A点高为h处的O点静止释放,从A点沿切线进入轨道,B处有一装置,小钢球向右能无能量损失的通过,向左则不能通过且小钢球被吸在B点。若小钢球能够运动到H点,则被等速反弹。各圆轨道半径均为R=0.6m,BC长L=2m,水平直轨道BC和GH的动摩擦因数μ=0.5,其余轨道均光滑,小钢球通过各圆弧轨道与直轨道相接处均无能量损失。某次游戏时,小钢球从O点出发恰能第一次通过圆弧的最高点E。(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
(1)小钢球第一次经过C点时的速度大小vC;
(2)小钢球第一次经过圆弧轨道最低点B时对轨道的压力大小FB(保留两位小数);
(3)若改变小钢球的释放高度h,求出小钢球在斜面轨道上运动的总路程s与h的函数关系。
22.(2022•浙江模拟)如图所示,倾斜轨道AB与水平直轨道BCDOMN在B处平滑连接,C、D间安装着水平传送带,C、D为两轮切点,间距L=6m,皮带轮半径r=0.1m;Q处安装着半径R=1m的竖直光滑圆轨道,在底部O处微微错开;N处安装着竖直弹性挡板。质量m=0.1kg的小滑块由A点以初速度v0=6m/s滑下,经传送带和圆轨道后与挡板相撞,撞后原速率弹回。滑块与传送带间的动摩擦因数μ1=0.2,与MN间的动摩擦因数为μ2=0.4,其余轨道均光滑。已知A点离地面高度h=1.5m,MN段的长度s=4.5m,g=10m/s2,滑块视为质点,空气阻力不计。
(1)若传送带静止,求滑块经过与圆心O等高的P点时对轨道的压力;
(2)若皮带轮以角速度ω1=20rad/s逆时针匀速转动,在滑块经过传送带的过程中,求滑块损失的机械能;
(3)若皮带轮以角速度ω2=90rad/s顺时针匀速转动,求滑块最后静止时离M点的距离;
(4)在皮带轮顺时针匀速转动的情况下,求滑块在MN段内滑行的总路程x与角速度ω的关系式
2021-2023年浙江省高考物理模拟试题分类——专题7机械能守恒定律 计算题
参考答案与试题解析
一.试题(共22小题)
1.(2022•温州二模)我国选手谷爱凌在北京冬奥会自由式滑雪好U形场地技巧决赛中夺得金牌。如图所示,某比赛用U形池场地长度L=160m、宽度d=20m、深度h=7.25m,两边竖直雪道与池底平面雪道通过圆弧雪道连接组成,横截面像“U”字形状,池底雪道平面与水平面夹角为θ=20°。为测试赛道,将一质量m=1kg的小滑块从U形池的顶端A点以初速度v0=0.7m/s滑入;滑块从B点第一次冲去U形池,冲出B点的速度vB=10m/s,与竖直方向夹角为α (α未知),再从C点重新落回U形池(C点图中未画出)。已知A、B两点间直线距离为25m,不计滑块所受的空气阻力,sin20°=0.34,cos20°=0.94,tan20°=0.36。
(1)A点至B点过程中,求小滑块克服雪道阻力所做的功Wf;
(2)忽略雪道对滑块的阻力,若滑块从池底平面雪道离开,求滑块离开时速度v的大小;
(3)若保持vB大小不变,调整速度vB与竖直方向的夹角为α0时,滑块从冲出B点至重新落回U形池的时间最长,求tanα0。
【解答】解:(1)小滑块从A点至B点过程中,由动能定理得:mgxsinθ-Wf=12mvB2-12mv02,由几何关系:x=xAB2-d2,解得:Wf=1.35J;
(2)忽略雪道对滑块的阻力,滑块从A点运动到池底平面雪道离开的过程中,由动能定理得:mgLsinθ+mghcosθ=12mv2-12mv02,代入数据得:v=35m/s;
(3)当滑块离开B点后设速度方向与U形池斜面的夹角为θ,沿U形池斜面方向分解速度及加速度vy=vBsinθ,vx=vBcosθ,ay=gcos(20°),ax=gsin(20°),vy=ayt1,t=2t1,由此可知,当vy最大时,滑块从冲出B点至重新落回U形池的时间最长,此时vB垂直于U形池斜面,即α0=20°,tanα0=sinα0cosα0=0.340.94=1747。
答:(1)小滑块克服雪道阻力所做的功为1.35J;
(2)滑块离开时速度v的大小为35m/s;
(3)tanα0为1747滑块从冲出B点至重新落回U形池的时间最长。
2.(2022•宁波二模)如图所示,在竖直平面内,某一游戏轨道由直轨道AB、光滑圆弧细管道BCD和光滑圆弧轨道DE平滑连接组成,两段圆弧半径相等R=0.5m,B、D等高,图中θ角均为37°,AB与圆弧相切,AM水平。直轨道AB上方有与AB相平行的匀强电场E=108N/C,且电场只分布在AB之间。直轨道AB底端装有弹射系统(弹簧长度很短,长度和质量不计,可以认为滑块从A点射出),具有初始弹性势能EP=2.5J,某次弹射系统将尺寸略小于管道内径的带正电的滑块弹出,冲上直轨道AB,直轨道AB上铺有特殊材料,使滑块与轨道AB间的动摩擦因数μ大小可调。滑块进入光滑圆轨道后,最后能在E点与弹性挡板相互作用后以等速率弹回。已知滑块的质量为m=0.1kg,带电量为q=+8.0×10﹣9C,B点的高度h=1.8m,整个过程中滑块可视为质点,所带电量保持不变,sin37°=0.6,cos37°=0.8。
(1)若调节AB间的特殊材料,使其变为光滑,求滑块在最高点C点时对轨道的作用力;
(2)现调节AB间的动摩擦因数μ,求滑块首次到达E点时的速率vE与μ之间的关系式;
(3)若滑块与弹性挡板相碰后最终能静止在轨道AB的中点,求动摩擦因数μ。
【解答】解:(1)由几何关系可得AB的长度为:l=hsinθ=1.80.6m=3m
由A点到C点的动能定理:EP+Eql-mgh-mgR(1-cosθ)=12mvC2
在C点根据牛顿运动定律:FN+mg=mvC2R
解得:FN=11N
牛顿第三定律:FN′=FN=11N,方向:竖直向上
(2)由A点到C点的动能定理:EP+Eql-mgh+mgR(1-cosθ)-μmgcosθ⋅l=12mvE2-0
解得:vE=64-48μ(ms)
考虑到滑块需先过C点:EP+Eql﹣mgh﹣mgR(1﹣cosθ)﹣μmgcosθ⋅l≥0
所以:μ≤54
所以:vE=64-48μ(且μ≤54)
(3)滑块经多次碰撞,最终在轨道AB中点速度减为0,由动能定理可得:
EP+Eq12-mgh2-μmgcosθ⋅(32l+nl)=0,其中n=0,1,2,3…
解得:μ=73(2n+3),其中n=0,1,2,3…
要让滑块在中点能停住:Eq﹣mgsinθ≤μmgcosθ
所以:μ≥14
因此,只有n=0,1,2,3时满足条件
所以动摩擦因数μ只能取79,715,13,727这4个值
答:(1)若调节AB间的特殊材料,使其变为光滑,滑块在最高点C点时对轨道的作用力为11N;
(2)现调节AB间的动摩擦因数μ,求滑块首次到达E点时的速率vE与μ之间的关系式为vE=64-48μ(且μ≤54);
(3)若滑块与弹性挡板相碰后最终能静止在轨道AB的中点,动摩擦因数μ只能取79,715,13,727这4个值。
3.(2023•镇海区校级模拟)如图所示,在水平直轨道上竖直放置一半径R=1m的圆形光滑轨道和细管弯成两个半圆组成的反“S”形光滑轨道,其半径r=0.05m。两轨道最低点B、D相距L1=4m,B、D间铺设特殊材料,其动摩擦因数μ1=0.2+0.2x(x表示DB上一点到B的距离)。一个质量为1kg可视为质点的小球P从倾角θ=37°、动摩擦因数μ3=0.8的斜面上以初动能Ek0滑下,经A点无能量损失进入长度L2=3m、动摩擦因数为μ2=0.2的AB直轨道,然后冲上圆形轨道。小球P释放点到水平轨道的高度h=3m,圆形轨道最低点B处入、出口靠近且相互错开,不计空气阻力。提示:可以用F﹣x图像下的“面积”代表力F做的功。
(1)若小球P恰好通过圆形轨道最高点C,求小球在B点对轨道的压力大小;
(2)调整释放初动能Ek0,使小球P离开反“S”形轨道最高点E后第一次落到水平直轨道上离E点的水平位移大小s=1m,求初动能Ek0的大小;
(3)调整释放初动能Ek0,要使小球P整个运动过程中不脱离轨道,且不停在水平轨道AB段上,求Ek0的取值范围。
【解答】解:(1)小球P恰好通过圆形轨道最高点C点,则有mg=mvC2R
解得vC=10m/s
从C到B,根据动能定理有2mgR=12mvB2-12mvC2
解得vB=50m/s
B点,则有FN-mg=mvB2R
解得FN=60N
根据牛顿第三定律,小球在B点对轨道的压力大小为60N;
(2)根据平抛运动规律有4r=12gt2,s=vEt
联立解得t=0.2s,vE=5m/s
BD上,有Ff=μ1mg=mg(0.2+0.2x)=2+2x
则摩擦力做功为WFf=2+102×4J=24J
从初始到E,则有mgh-μ3mghtan37°-μ2mgL2-WFf-mg4r=12mvE2-Ek0
解得Ek0=46.5J
(3)①恰好到A,则有mgh-μ3mghtan37°=0-Ek0
解得Ek0=2J
所以0≤Ek0≤2J
②恰好到O点等高处,则有mgh-μ3mghtan37°-μ2mgL2-mgR=0-Ek0
解得Ek0=18J
返回恰好到A,则有mgh-μ3mghtan37°-2μ2mgL2=0-Ek0
解得Ek0=14J
所以14J≤Ek0≤18J
③恰好过C,vC=10m/s,则有mgh-μ3mghtan37°-μ2mgL2-2mgR=12mvC2-Ek0
解得Ek0=33J
恰好到E,则有mgh-μ3mghtan37°-μ2mgL2-WFf-mg4r=0-Ek0
解得Ek0=34J
所以33J≤Ek0≤34J
综上,0≤Ek0≤2J或者14J≤Ek0≤18J或者33J≤Ek0≤34J
答:(1)小球在B点对轨道的压力大小为60N;
(2)初动能Ek0的大小为46.5J;
(3)Ek0的取值范围为0≤Ek0≤2J或者14J≤Ek0≤18J或者33J≤Ek0≤34J。
4.(2023•温州模拟)2022年10月,某学校举办校运动会,在铅球比赛场地上放置了一个铅球回收架,以便于回收选手投出的铅球。图1所示是铅球回收架的最后一段轨道,可简化为如图2所示的ABCDE轨道,其中AB、BC、CD轨道均为直轨道且平滑连接,长度分别为LAB=1.0m、LBC=1.6m、LCD=0.6m,与水平方向的夹角分别为θ1=37°、θ2=15°、θ3=37°。一质量m=4kg的铅球,从A点以某一速度冲上AB轨道,运动到B点时速度恰好为0,然后经过BC轨道冲上CD轨道。若铅球在AB、CD轨道运动时所受的轨道阻力恒为Ff1=8N,在BC轨道运动时所受的轨道阻力恒为Ff2=9.6N,不计其它阻力,铅球大小可忽略。(取sin37°=0.6,cos37°=0.8,sin15°=0.26,cos15°=0.96),求铅球
(1)冲上AB轨道时的初速度大小vA;
(2)运动到轨道C点时的速度大小vc;
(3)从轨道A点到在CD轨道上速度第一次减为零时所用的总时间t总。
【解答】解:(1)铅球在AB段的加速度大小为a1=mgsinθ1+Ff1m
由运动学公式2a1xAB=vA2
联立解得vA=4m/s
(2)铅球在BC段的加速度大小为a2=mgsinθ2-Ff2m
由运动学公式2a2xBC=vC2
联立解得vC=0.8m/s
(3)铅球在CD段的加速度大小为a3=mgsinθ3+Ff1m
铅球在CD轨道上速度第一次减为零时所用的时间为t1=vCa3
铅球在BC轨道上的时间为t2=vCa2
铅球在AB轨道上的时间为t3=vAa1
联立解得t1=0.1s,t2=4s,t3=0.5s
从轨道A点到在CD轨道上速度第一次减为零时所用的总时间t总=t1+t2+t3
解得t总=4.6s
答:(1)冲上AB轨道时的初速度大小4m/s;
(2)运动到轨道C点时的速度大小0.2m/s;
(3)从轨道A点到在CD轨道上速度第一次减为零时所用的总时间4.6s。
5.(2023•浙江模拟)某闯关项目的简化图如图所示,距离水平地面高为h=1.8m的平台上,A点左侧为光滑平台,一根弹簧左端与固定挡板连接,自然长度时右端不超过A点,一个可以看作质点的滑块靠着弹簧右端(不拴连),滑块质量为m=1kg。平台AB段长为L1=2.0m,与滑块的动摩擦因数为μ1=0.1。B点右侧设置长为L2=1.5m的水平传送带,传送带与滑块的动摩擦因数为μ2,传送带的右端设置半径为R=0.9m的半圆弧光滑轨道,CD为竖直直径的上下两端,C点与传送带末端的空隙很小,但是可以让滑块通过。传送带一且启动,顺转(即让传送带顺时针方向转动)和逆转的速度都为v=4m/s,在B点的左侧附近设置传送带启动按钮,按钮有两个,一个为顺转,一个为逆转。闯关开始前传送带处于关闭状态。闯关时,选手首先向左推滑块压缩弹簧,使弹簧具有一定的初始弹性势能EP,然后释放滑块,在滑块进入传送带前,选手必须按照实时情况按下顺转按钮或逆转按钮。闯关规则为:如果滑块最终能始终沿着轨道到达水平地面,则闯关成功;如果滑块最终退回到A点左侧,则可以再次闯关(既不失败,也没有成功);如果滑块最终停在AB段上,或者向右出传送带后摔落在CD段则游戏失败(来不及按下按钮也视为失败,本题假设选手都按了按钮)。g取10m/s2。
(1)设备调试时,关闭传送带,测得当弹簧的初始弹性势能为EP=5.0J时,滑块恰好滑到传送带的右端停止,求传送带与滑块的动摩擦因数μ2的大小;
(2)某选手压缩弹簧使其具有EP=4.5J的初始弹性势能,请通过计算说明本次闯关选手(按下任何一个按钮的可能性都会有)是否可能会失败;
(3)求选手按下任意一个按钮都能闯关成功的初始弹簧弹性势能EP取值范围。
【解答】解:(1)该过程中,根据能量守恒定律可得:
Ep=μ1mgL1+μ2mgL2
代入数据解得:μ2=0.2
(2)设滑块到达B点的速度为vB,根据能量守恒定律可得:
Ep-μ1mgL1=12mvB2
解得:vB=3m/s
选择1:若选手按下顺转按钮,设滑块在传送带上能全程加速,到达C点的速度为vC,根据动能定理可得:
μ2mgL2=12mvC2-12mvB2
解得:vC=11m/s
vC<v,说明全程加速成立
vC>v0,说明按下顺转按钮可以沿轨道到达水平地面,闯关成功
选择2:若选手按下逆转按钮,设滑块在传送带上减速到零的对地位移为x,则
-μ2mgx=0-12mvB2
解得:x=1.25m
因为x<L2,说明传送带上减速到零的假设成立
vB=5m/s<v,说明滑块可以按原速率v0=5m/s回到B点
又12mvB2=12×1×5J=2.5J>μ1mgL1=0.1×1×10×2J=2J
故滑块可以回到A点左侧,再闯关一次
综上分析,本次选手闯关不会失败
(3)设顺转按钮情景下的最小初始弹性势能为Ep1
有Ep1-μ1mgL1+μ2mgL2=12mv02
解得:Ep1=3.5J
且Ep1=3.5J≥μ1mgL1=2J,能够冲上传送带,成立
设逆转按钮情景下的最小初始弹性势能为Ep2
Ep2-μ1mgL1-μ2mgL2=12mv02
解得:Ep2=9.5J
综上所述,选手按下任意一个按钮都能闯关成功的初始弹簧弹性势能EP取值范围为Ep≥9.5J
答:(1)传送带与滑块的动摩擦因数μ2的大小为0.2;
(2)通过分析可知,本次选手闯关不会失败;
(3)选手按下任意一个按钮都能闯关成功的初始弹簧弹性势能EP取值范围为Ep≥9.5J。
6.(2022•宁波模拟)如图所示,一游戏装置由安装在水平台面上的高度h可调的斜轨道AB、竖直圆轨道(在最低点E分别与水平轨道AE和EG相连)、细圆管道GHIJ(HI和IJ为两段四分之一圆弧)和与J相切的水平直轨道JK组成。可认为所有轨道均处在同一竖直平面内,连接处均平滑。已知,滑块质量为m=30g且可视为质点,竖直圆轨道半径为r=0.45m小圆弧管道HI和大圆弧管道IJ的半径之比为1:4,L1=1.5m不变,L2=0.5m,滑块与AB、EG及JK间摩擦因数均为μ=0.5,其他轨道均光滑,不计空气阻力,忽略管道内外半径差异。现调节h=2m,滑块从B点由静止释放后,贴着轨道恰好能滑上水平直轨道JK,求:
(1)大圆弧管道IJ的半径R;
(2)滑块经过竖直圆轨道与圆心O等高的P点时对轨道的压力F1与运动到圆弧管道最低点H时对轨道的压力F2大小之比;
(3)若在水平轨道JK上某一位置固定一弹性挡板,当滑块与之发生弹性碰撞后能以原速率返回,若第一次返回时滑块不脱轨就算游戏闯关成功。调节斜轨道的高度为h=3m,仍让滑块从B点由静止滑下,问弹性挡板与J的间距L满足什么条件时游戏能闯关成功。
【解答】解:(1)物块从B点开始下滑,恰能达到水平直轨道JK,根据动能定理得:
mgh-μmg(L1+L2)-mg(R+14R)=0-0
解得:R=0.8m
(2)运动到P点时,根据动能定理得:
mgh-μmgL1-mgr=12mvP2
在P点时,F1=mvP2r
解得:vP=4m/s;F1=1615N
运动到H点时
mgh-μmg(L1+L2)=12mvH2
F1-mg=mvH214R
解得:F2=3.3N
因此F1F2=3299
(3)要想让物块无挡板碰后不脱离圆轨道,当L最大时对应于物块恰能达到与圆轨道圆心O等高的位置,则由动能定理得:
mgh﹣μmg(L1+2L2+2Lmax)﹣mgr=0
解得:Lmax=1.3m
当L最小时对应于物块恰能达到与圆轨道最高点的位置,此时
mg=vF2r
则由动能定理得:mgh-μmg(L1+2L2+2Lmin)-2mgr=12mvF2
解得:Lmin=0.625m
则弹性挡板与J的间距L满足L≤0.625m或者L≥1.3m才能闯关成功。
答:(1)大圆弧管道IJ的半径为0.8m;
(2)滑块经过竖直圆轨道与圆心O等高的P点时对轨道的压力F1与运动到圆弧管道最低点H时对轨道的压力F2大小之比为32:99;
(3)弹性挡板与J的间距L满足满足L≤0.625m或者L≥1.3m才能闯关成功。
7.(2021•瓯海区校级模拟)如图所示,在高h1=30m的水平平台上有一质量m=1kg的小物块(可视为质点),它在F=20N的水平外力作用下从离平台右端l=5m处由静止开始向右做直线运动,物块与平台间的动摩擦因数μ0=0.2,作用一段距离x后撤去力F,物块又滑行一段距离后从平台右端水平抛出,物块抛出后,恰好能从光滑圆弧形轨道BC的B点沿切线方向进入圆弧形轨道。B点的高度h2=15m,圆弧轨道的圆心O与平台等高,轨道最低点C的切线水平,并与地面上长度L=70m的水平粗糙轨道CD平滑连接;小物块沿轨道BCD运动并与右边墙壁发生碰撞,取g=10m/s2。
(1)求水平外力F的作用的距离x;
(2)若小物块与墙壁只发生一次碰撞,碰后物块的速度等大反向、反向运动过程中物块没有冲出B点,最后停在轨道CD上的P点(P点没画出),设小物块与轨道CD之间的动摩擦因数为μ,求μ的取值范围。
【解答】解:(1)设OB与OC的夹角为θ,由平抛运动规律得
vy2=2g(h1﹣h2)
tanθ=vyvx
由几何关系得
cosθ=h1-h2h1
联立代入数据解得
vy=103m/s,vx=10m/s
由开始到A点,由动能定理得
Fx﹣μ0mgl=12mvx2
联立代入数据解得:x=3m
(2)物块第一次到达B点的速度为:v=vx2+vy2
当物块刚好第二次能到达D点时,摩擦因数最小,全程动能定理得
mgh2﹣μ′mg•3L=0-12mv2
联立代入数据解得:μ′=16
当物块刚好第一次能到达D点时,摩擦因数最大,全程动能定理得
mgh2﹣μ′'mgL=0-12mv2
代入数据解得:μ′'=12
则μ的取值范围为:16≤μ<12
答:(1)求水平外力F的作用的距离为3m;
(2)μ的取值范围为16≤μ<12。
8.(2023•嘉兴一模)如图所示,某游乐场游乐装置由竖直面内轨道BCDE组成,左侧为半径R=0.8m的光滑圆弧轨道BC,轨道上端点B和圆心O的连线与水平方向的夹角α,下端点C与粗糙水平轨道CD相切,DE为倾角θ=37°的粗糙倾斜轨道,一轻质弹簧上端固定在E点处的挡板上。现有质量为m=0.1kg的小滑块P(视为质点)从空中的A点以v0=22m/s的初速度水平向左抛出,经过65s后恰好从B点沿轨道切线方向进入轨道,沿着圆弧轨道运动到C点之后继续沿水平轨道CD滑动,经过D点后沿倾斜轨道向上运动至F点(图中未标出),弹簧恰好压缩至最短,已知CD=DF=1m,滑块与轨道CD、DE间的动摩擦因数为μ=0.1,各轨道均平滑连接,不计其余阻力,sin37°=0.6。求:
(1)BO连线与水平方向的夹角α的大小;
(2)小滑块P到达与O点等高的O'点时对轨道的压力;
(3)弹簧的弹性势能的最大值;
(4)试判断滑块返回时能否从B点离开,若能,求出飞出时对B点的压力大小;若不能,判断滑块最后位于何处。
【解答】解:(1)滑块从A到B做平抛运动,滑块经过B点时的竖直分速度为vy=gt=10×65m/s=26m/s
滑块恰好从B点进入轨道,如图所示,由平抛运动的规律有
v0=vBsinα=vytanα
解得:α=30°,vB=42m/s
(2)由B→O',由动能定理可知
mgRsin30°=12mvO'2-12mvB2
解得vO'=210m/s
滑块经过O'点时受轨道的支持力大小FN,由牛顿第二定律有FN=mvO'2R
解得FN=5N
由牛顿第三定律可得滑块在O'点时对轨道的压力大小F压=5N,方向向左。
(3)设CD=DF=L,从B到F,由动能定理及功能关系有
mg(R+Rsinα﹣Lsinθ)﹣μmgL﹣μmgLcosθ﹣Ep=0-12mvB2
代入数据可解得弹簧的弹性势能的最大值:Ep=2.02J
(4)设滑块返回时能上升的高度为h,由功能关系有
mgLsinθ+Ep=mgLcosθ+μmgL+mgh
解得h=2.44m>1.2m
则滑块返回时能从B点离开。
运动到B点时,有:mgh=mg(R+Rsinα)+12mvB2,
在B点,对滑块,由牛顿第二定律得
mgsinα+FN=mvB2R
解得:FN=2.6N
由牛顿第三定律可知对B点的压力为F'N=2.6N
答:(1)BO连线与水平方向的夹角α的大小为30°;
(2)小滑块P到达与O点等高的O'点时对轨道的压力为5N,方向向左;
(3)弹簧的弹性势能的最大值为2.02J;
(4)能,飞出时对B点的压力大小为2.6N。
9.(2023•浙江模拟)如图所示,半径R=2.45m的竖直光滑14圆弧轨道AB,其底端右侧是一个凹槽,凹槽右端连接一个半径r=0.40m的光滑圆轨道,轨道固定在竖直平面内,D与圆心连线与竖直方向成θ=37°角。一质量为m=1kg的滑板Q放置在凹槽内水平面上,其上表面刚好与B点和C点水平等高。开始时滑板静置在紧靠凹槽左端处,此时滑板右端与凹槽右端的距离d=0.60m。一质量也为m的小物块P(可视为质点)从A点由静止滑下,当物块滑至滑板右端时滑板恰好到达凹槽右端,撞击后滑板立即停止运动。已知物块与滑板间的动摩擦因数μ=0.75,其余接触面的摩擦均可忽略不计,取重力加速度g=10m/s2。
(1)求滑块滑至B点时对B点的压力;
(2)求滑板的长度l;
(3)请通过计算说明滑块滑上CD轨道后能否从D点飞出?
【解答】解:(1)滑块由A→B过程,由动能定理可得
mgR=12mv02
解得:v0=7m/s
滑块滑至B点,由牛顿第二定律得
FN-mg=mv02R
解得:FN=30N
由牛顿第三定律可得滑块对B点的压力大小F压=FN=30N,方向竖直向下。
(2)滑块在滑板上运动时,根据牛顿第二定律可得小物块P的加速度大小为
a1=μmgm=μg=0.75×10m/s2=7.5m/s2
滑板Q的加速度大小为a2=μmgm=μg=0.75×10m/s2=7.5m/s2
根据题意可知,从滑块滑上滑板Q到滑板右端到达凹槽右端过程,滑块P一直做匀减速运动,滑板Q一直做匀加速运动,设运动时间为t.
对于滑板Q,有d=12a2t2
解得:t=0.4s
对于滑块P,有x=v0t-12a1t2
解得:x=2.2m
故滑板的长度为l=x﹣d=2.2m﹣0.60m=1.6m
(3)滑块P到达半圆轨道最低点C时的速度为v1=v0﹣a1t=(7﹣7.5×0.4)m/s=4m/s
设滑块P可以到达D点,根据机械能守恒定律可得
12mv12=mgr(1+cos37°)+12mv22
解得滑块P在D点速度为v2=1.6m/s
假设P刚好到达D点,则由牛顿第二定律得
mgcos37°=mvD2r
解得P在D点的最小速度为vD=3.2m/s>v2
说明小物块P到不了D点。
答:(1)滑块滑至B点时对B点的压力为30N,方向竖直向下;
(2)滑板的长度l为1.6m;
(3)滑块滑上CD轨道后不能从D点飞出。
10.(2022•杭州二模)公交站点1与站点2之间的道路由水平路面AB段、CD段及倾角为15°的斜坡BC段组成,斜坡足够长。一辆公交车额定功率为210kW,载人后总质量为8000kg。该车在AB段以54km/h的速率匀速行驶,此过程该车的实际功率为额定功率的一半。该车到达C点时的速率为21.6km/h,此后在大小恒为1.4×104N的牵引力作用下运动,直到速度达到54km/h时关闭发动机自由滑行,结果该车正好停在了D点(站点2)。若在整个行驶过程中,公交车的实际功率不超过额定功率,它在每一个路段的运动都可看成直线运动,它受到的由地面、空气等产生的阻力F1大小不变。已知sin15°=0.26,求:
(1)F1的大小;
(2)公交车上坡过程中能够保持匀速行驶的最大速率;
(3)C点与D点之间的距离。
【解答】解:(1)AB段,已知v=54km/h=15m/s,
由于AB匀速行驶,根据P=Fv,
可知F1=P额2v=210×103215N=7000N,
(2)BC段,根据P=Fv可知,当达到最大速度时F=F1+mgsin15°
即P额=(F1+mgsin15°)vmax,得vmax=P额F1+mgsin15°=210×1037000+8000×10×0.26m/s≈7.55m/s≈27.2km/h,
即公交车上坡过程中能够保持匀速行驶的最大速率约为27.2km/h;
(3)CD段,已知21.6km/h=6m/s
速度达到54km/h之前,应用动量定理(F﹣F1)t1=mv﹣mvC,得t1=mv-mvCF-F1=8000×15-8000×61.4×104-7000s≈10.3s
关闭发动机自由滑行过程,应用动量定理﹣F1t2=0﹣mv,得t2=mvF1=8000×157000s=17.1s
速度达到54km/h之前,v1=v+vc2=15+62m/s=10.5m/s,
关闭发动机自由滑行过程,平均速度为v=v2=152m/s=7.5m/s,
C点与D点之间的距离x=v1t1+vt2=10.5×10.3m+7.5×17.1m=236.4m
答:(1)F1的大小为7000N;
(2)公交车上坡过程中能够保持匀速行驶的最大速率约为27.2km/h;
(3)C点与D点之间的距离为236.4m。
11.(2021•浙江模拟)有一弹射打板游戏装置,其结构如图所示,半径R=0.4m的竖直光滑圆弧轨道BC固定在水平底座CD上,轨道的上端点B和圆心O的连线与水平方向的夹角θ=30°,C、D两点间的距离L=1.2m;D点与弹射装置相连,弹射装置的弹性势能Ep=2.0J。装置的上方有一高h=0.4m可水平移动的竖直挡板,挡板的下端点A与BC轨道有一定间距。在某次游戏中,一质量m0=0.1kg的弹射物(可视为质点)从弹射器弹出,经DC沿圆弧轨道从B点抛出,恰好从A点贴近挡板水平飞出,已知弹射物与水平面间的动摩擦因数μ=0.5,不计空气阻力,g取10m/s2求:
(1)弹射物经过圆弧轨道上C点时对轨道的压力;
(2)弹射物经过圆弧轨道上B点时的速度vB的大小:
(3)挡板的下端点A与轨道最高点B的高度差:,
(4)现减小弹射物的质量,并且要求弹射物与挡板垂直相碰,试写出挡板水平距离×(A与B点的水平间距)与弹射物的质量m的函数关系。
【解答】解:(1)从D到C,由动能定理:Ep﹣μm0gL=12m0vc2-0,得:v c2=28m2/s2,在C点,由牛顿第二定律:F-m0g=m0vc2R,解得:F=8N,由牛顿第三定律可得,弹射物对轨道压力大小为8N,方向竖直向下。
(2)从C到B,由动能定理:﹣mgR(1+sinθ)=12mvB2-12mvc2,联立得:vB=4m/s
(3)B点速度如图所示:v1=vBcosθ=23m/s,竖直方向是竖直上抛运动,h=v122g=(23)22×10m=0.6m
(4)从D到B,由动能定理:EP﹣μmgL﹣mgR(1+sinθ)=12mvB2-0,解得:vB=21-6mm,垂直打到板上时间:t=v1g=vBcosθg,A点到B点的水平间距:
x=vBsinθ•t=vB2sinθcosθg=3(1-6m)mg,当m=0.1kg时,x最小,xmin=235m,当与挡板最高点碰时,x最大,0.6+h=v122g=vB2cos2θ2g,解得:vB=4153m/s,所以
xmax=233m,即A点到B点的水平间距:x=3(1-6m)mg(235m≤x≤233m)
答:(1)弹射物经过圆弧轨道上C点时对轨道的压力为8N,方向竖直向下;
(2)弹射物经过圆弧轨道上B点时的速度vB的大小为4m/s:
(3)挡板的下端点A与轨道最高点B的高度差为0.6m:,
(4)现减小弹射物的质量,并且要求弹射物与挡板垂直相碰,挡板水平距离×(A与B点的水平间距)与弹射物的质量m的函数关系为x=3(1-6m)mg(235m≤x≤233m)
12.(2022•浙江模拟)如图所示,质量均为m=4kg的两个小物块A、B(均可视为质点)放置在水平地面上,竖直平面内半径R=0.4m的光滑半圆形轨道与水平地面相切于C,弹簧左端固定。移动物块A压缩弹簧到某一位置(弹簧在弹性限度内),由静止释放物块A,物块A离开弹簧后与物块B碰撞并粘在一起以共同速度v=5m/s向右运动,运动过程中经过一段长为s,动摩擦因数μ=0.2的水平面后,冲上圆轨道,除s段外的其他水平面摩擦力不计。求:(g取10m/s2)
(1)若s=1m,两物块刚过C点时对轨道的压力大小;
(2)若两物块能冲上圆形轨道,且不脱离圆形轨道,s应满足什么条件。
【解答】解:(1)设两物块经过C点时速度为vC,两物块受到轨道支持力为FNC。
A与B从粘合后到运动到C点的过程,由动能定理得:
﹣2μmgs=12×2mvC2-12×2mv2
在C点,对AB整体,由牛顿第二定律得:
FNC﹣2mg=2mvC2R
代入数据解得:FNC=500N
由牛顿第三定律知,两物块对轨道压力大小也为500N。
(2)两物块不脱离轨道有两种情况:①能过轨道最高点,设两物块经过半圆形轨道最高点最小速度为v1,则
2mg=2mv12R,得:v1=gR=10×0.4m/s=2m/s
两物块从碰撞后到经过最高点过程中,由功能关系有:
12×2mv2﹣2μmgs﹣4mgR≥12×2mv12
代入解得s满足条件:s≤1.25m
②两物块上滑最大高度不超过14圆弧,设两物块刚好到达14圆弧处速度为v2=0,两物块从碰撞后到最高点,由功能关系有:
12×2mv2﹣2μmgs≤2mgR
同时依题意,两物块能滑出粗糙水平面,由功能关系:12×2mv2>2μmgs
代入解得s满足条件:4.25m≤s<6.25m。
答:(1)两物块刚过C点时对轨道的压力大小为500N。
(2)s应满足的条件是:s≤1.25m或4.25m≤s<6.25m。
13.(2021•岱山县校级模拟)如图所示,水平放置的轻质弹簧原长为2L,一端与质量m1=2kg的物块P接触但不连接,另一端固定在A点,光滑水平轨道AB长度为5L.长度为L0=2.5m的水平传送带分别与B端和水平光滑轨道CD平滑连接,物块P与传送带之间的动摩擦因数μ=0.2,传送带始终以v=2m/s的速率顺时针匀速转动.质量为m2=6kg小车放在光滑水平轨道上,位于CD右侧,小车左端与CD段平滑连接,小车的水平面长度L1=0.5m,右侧是一段半径R=0.5m的四分之一光滑圆弧,物块P与小车水平上表面的动摩擦因数μ1=0.1.用外力推动物块P,将弹簧压缩至长度L,然后放开,P开始沿轨道运动,冲上传送带后开始做减速运动,到达传送带右端时速度恰好与传送带速度大小相等.重力加速度大小g=10m/s2.求:
(1)弹簧压缩至长度L时储存的弹性势能Ep;
(2)物块P在小车圆弧上上升的最大高度H;
(3)要使物块P既可以冲上圆弧又不会从小车上掉下来,小车水平面长度的取值范围。
【解答】解:(1)设物块P离开弹簧时的速度为v0,在物块与弹簧相互作用过程中,由机械能守恒定律:Ep=12m1v02①
物块在传送带上运动过程中,由动能定理有:-μm1gL0=12m1v2-12m1v02②
联立①②代入数据可得:Ep=14J;
(2)当物块运动到小车的最高点时,对于P与小车构成的系统水平方向动量守恒,设物块与小车有共同速度v1,
取向右为正方向,根据动量守恒定律可得:m1v=(m1+m2)v1③
由能量守恒定律有:12m1v2=12(m1+m2)v12+m1gH+μ1m1gL1④
联立③④代入数据可得:H=0.1m;
(3)设当小车水平面长度为L2时,物块到达小车水平右端时与小车的共同速度仍然为v1,
根据能量关系可得:12m1v2=12(m1+m2)v12+μ1m1gL2⑤
联立③⑤代入数据可得:L2=1.5m
设当小车水平长度为L3时,物块到达小车水平左端时与小车有共同速度,
根据能量关系可得:12m1v2=12(m1+m2)v12+2μ1m1gL3⑥
联立③⑥代入数据可得:L3=0.75m
要使物块P既可以冲上圆弧又不会从小车上掉下宋,小车水平长度的取值范围:0.75m≤L≤1.5m。
答:(1)弹簧压缩至长度L时储存的弹性势能为14J;
(2)物块P在小车圆弧上上升的最大高度为0.1m;
(3)要使物块P既可以冲上圆弧又不会从小车上掉下来,小车水平面长度的取值范围为0.75m≤L≤1.5m。
14.(2021•金华模拟)如图所示,竖直放置的半径为R=0.2m的螺旋圆形轨道BGEF与水平直轨道MB和BC平滑连接,倾角为θ=30°的斜面CD在C处与直轨道BC平滑连接。水平传送带MN以v0=4m/s的速度顺时针方向运动,传送带与水平地面的高度差为h=0.8m,MN间的距离为LMN=3.0m,小滑块P与传送带和BC段轨道间的摩擦因数μ=0.2,轨道其他部分均光滑。直轨道BC长LBC=1m,小滑块P质量为m=1kg。
(1)若滑块P第一次到达圆轨道圆心O等高的F点时,对轨道的压力刚好为零,求滑块P从斜面静止下滑处与BC轨道高度差H;
(2)若滑块P从斜面高度差H=1.0m处静止下滑,求滑块从N点平抛后到落地过程的水平位移;
(3)滑块P在运动过程中能二次经过圆轨道最高点E点,求滑块P从斜面静止下滑的高度差H范围。
【解答】(1)滑块P在圆轨道F点的压力刚好为零,则vF=0,
由动能定理得:mg(H﹣R)﹣μmgLBC=0
解得:H=μLBC+R=0.2×1m+0.2m=0.4m
(2)H=1.0m,滑块运动到N点时的速度为vN
从开始到N点应用动能定理mgH-μmg(LBC+LBN)=12mvN2-0
解得vN=2m/s
从N点滑块做平抛运动,水平位移为x=vN2hg=2×2×0.810m=0.8m
(3)滑块P在运动过程中恰好能第一次经过E点必须具有的高度为H1
从开始到E点应用动能定理mgH1-μmgLBC-2mgR=12mvB2-0
在E点时有mg=mvE2R
解得H1=0.7m
滑块滑上传送带时的速度为vM,mgH1-μmgLBC=12mvM2-0,vM=10m/s<4m/s
滑块做减速运动的位移为L=vM22μg=2.5m<LMN
因此滑块返回M点时的速度也为vM=10m/s,因此第二次过E点.
设高度为H2时,滑块从传送带返回M点时的最大速度为v=2μgLMN=2×0.2×10×3.0m/s=12m/s
从开始到M点应用动能定理mgH2-μmgLBC=12mv2-0
解得H2=0.8m
二次经过E点后,当滑块再次返回圆轨道B点时速度为vB,mgH2-3μmgLBC=12vB2-0,vB=2m/s<10m/s,所以不会第三次过E点
能二次经过E点的高度H范围是0.7m≤H≤0.8m
答:(1)若滑块P第一次到达圆轨道圆心O等高的F点时,对轨道的压力刚好为零,则滑块P从斜面静止下滑处与BC轨道高度差H为0.4m;
(2)若滑块P从斜面高度差H=1.0m处静止下滑,滑块从N点平抛后到落地过程的水平位移为0.8m;
(3)滑块P在运动过程中能二次经过圆轨道最高点E点,滑块P从斜面静止下滑的高度差H范围是0.7m≤H≤0.8m。
15.(2022•浙江模拟)某游乐场的滑梯可以简化为如图所示竖直面内的ABCD轨道,AB为长L=6m、倾角α=37°的斜轨,BC为水平轨道,CD为半径R=15m、圆心角β=37°的圆弧,轨道AB段粗糙其余各段均光滑。一小孩(可视为质点)从A点以初速度v0=23m/s下滑,沿轨道运动到D点时的速度恰好为零(不计经过B点时的能量损失)。已知该小孩的质量m=30kg,取sin37°=0.6,cos37°=0.8,不计空气阻力,设最大静摩擦力等于滑动摩擦力。求:
(1)该小孩第一次经过圆弧C点时,对圆弧轨道的压力FN;
(2)该小孩在轨道AB上第一次从A下滑到B的时间t;
(3)若将AB段轨道改为圆弧形状(图中虚线部分,轨道材质不变),试定性说明题设条件下小孩在轨道上游玩时是否会冲出D点而发生危险?
【解答】解:(1)由C到D速度减为0,由动能定理可得
-mg(R-Rcos37°)=0-12mvC2
代入数据解得 vC=60m/s
在C点,对小孩受力分析,由牛顿第二定律得
FN﹣mg=mvC2R
代入数据解得 FN=420N
根据牛顿第三定律,知小孩对轨道的压力为420N,方向向下
(2)在A→C过程有:mgLsinα﹣μmgsLcosα=12mvC2-12mv02
代入数据解得:μ=0.25
从A→B,沿斜面下滑的过程中,由牛顿第二定律可得
mgsin37°﹣μmgcos37°=ma
代入数据解得
a=4m/s2
由运动学公式L=v0t+12at2
代入数据解得
t=2(15-3)4s
(3)AB段粗糙,若改为圆弧形状,长度变长,则摩擦力做功增加,速度减小更快,故到达不了D点。
答:(1)该小孩第一次经过圆弧C点时,对圆弧轨道的压力FN是420N,方向向下。
(2)小孩在轨道AB上第一次从A下滑到B的时间为2(15-3)4s;
(3)将AB段轨道改为圆弧形状不会有危险。
16.(2022•绍兴二模)如图甲所示为北京首钢滑雪大跳台,模型简化如图乙所示,AB 和EF是长为L1=50m的倾斜滑到,倾角为θ=37°,CD是长为L2=30m 的水平滑道,倾斜滑道AB、EF和水平滑道CD之间分别用一圆弧轨道连接,圆弧轨道半径为R=10m,圆心角为θ=37°,FG为结束区。一质量为m=90kg的运动员从A点静止滑下沿滑道ABCD运动,从D点沿水平方向滑离轨道后,完成空翻、回转等技术动作,落到倾斜轨道,最后停在结束区。为简化运动,运动员可视为质点,不计空气阻力。
(1)运动员刚好从D点沿水平方向滑离轨道,求运动员在D点的速度;
(2)在(1)情形下,求从开始运动到完成表演落到倾斜轨道过程中摩擦阻力做的功;
(3)运动员可以在滑道ABCD滑行过程中利用滑雪杖支撑前进,获取一定的能量ΔE,要使运动员安全停留在结束区,落到倾斜轨道上的动能不能超过15250J,求ΔE大小应满足的条件。
【解答】解:(1)运动员在D点能刚好离开轨道,即运动员受到的支持力为0.
在D点,有:mg=mvD2R
代入数据解得:vD=10m/s;
(2)从A点到D点的过程中,由动能定理得:mgh1+Wf=12mvD2
AD的高度差:h1=L1sin37°+R(1﹣cos37°)
联立解得:Wf=﹣24300J;
(3)设水平位移x,竖直下落距离为h,D点速度为v0,落到倾斜滑道上时,由平抛运动的规律可得:
x=v0t,h=12gt2
解得:h=gx22v02
由几何关系可得:h﹣R(1﹣cos37°)=(x﹣Rsin37°)tan37°
动能Ek=mgh+12mv02
代入各量,用h表示,得Ek=mg[h+(4h+10)236h]
当Ek=15250J,解得:h=10m
在整个运动过程中,根据能量守恒定律可得:mg(h1+h)+Wf+ΔE﹣Ek=0
代入数据解得:ΔE=1750J,即ΔE≤1750J。
答:(1)运动员刚好从D点沿水平方向滑离轨道,运动员在D点的速度为10m/s;
(2)在(1)情形下,从开始运动到完成表演落到倾斜轨道过程中摩擦阻力做的功为﹣24300J;
(3)要使运动员安全停留在结束区,落到倾斜轨道上的动能不能超过15250J,ΔE大小应满足ΔE≤1750J。
17.(2021•浙江模拟)简谐运动是一种常见且重要的运动形式。它是质量为m的物体在受到形如F=﹣kx的回复力作用下,物体的位移x与时间t遵循x=Asinωt变化规律的运动,其中角频率ω=2πT=km(k为常数,A为振幅,T为周期)。弹簧振子的运动就是其典型代表。
如图所示,一竖直光滑的管内有一劲度系数为k的轻弹簧,弹簧下端固定于地面,上端与一质量为m的小球A相连,小球A静止时所在位置为O,另一质量也为m的小球B从距A为H的P点由静止开始下落,与A发生瞬间碰撞后一起开始向下做简谐运动。两球均可视为质点,在运动过程中,弹簧的形变在弹性限度内,当其形变量为x时,弹性势能为Ep=12kx2,已知H=3mgk,重力加速度为g。求:
(1)B与A碰撞后瞬间一起向下运动的速度;
(2)小球A被碰后向下运动离O点的最大距离。
(3)小球A从O点开始向下运动到第一次返回O点所用的时间。
【解答】解:(1)小球B自由下落H的速度为vB
根据动能定理可得:mgH=12mvB2
解得:vB=2gH
小球B与小球A碰撞过程动量守恒,取向下为正,则有:
mvB+0=(m+m)v1
解得:v1=3mg22k;
(2)小球A在O位置,弹簧被压缩x0,则 x0=mgk
小球A与小球B共同体继续向下运动离O点的最大距离为xm,根据机械能守恒定律可得:
12(2m)v12+12kx02+2mgxm=12k(x0+xm)2
由mg=kx0
整理得:xm2-2x0xm-3x02=0
解得:xm=3x0,xm=﹣x0(舍去)
即:xm=3mgk;
(3)由题意振动周期:T=2π2mk,又振幅A=2x0=2mgk
所以平衡位置在弹簧压缩2x0处,从碰撞后开始到再次回到O点的振动图象如图:
从O点开始到平衡位置经过的时间t1=13×14T=112T
所求时间t=2t1+12T=23T
解得:t=23×2π2mk=4π32mk。
答:(1)小球B与小球A碰撞后瞬间一起向下运动的速度为3mg22k;
(2)小球A被碰后向下运动离O点的最大距离3mgk;
(3)小球A从O点开始向下运动到第一次返回O点所用的时间4π32mk。
18.(2021•宁波二模)如图所示是一弹射游戏装置,由安装在水平台面上的固定弹射器、竖直圆轨道(在最低点A、C分别与水平轨道OA和CD相连)、倾斜长轨道DE组成。游戏时滑块从O点弹出后,经过圆轨道并滑上倾斜长轨道DE,若滑块从长轨道DE滑下则反向进入圆轨道,从圆轨道滑出,进入AO轨道并压缩弹射器的弹簧,随后能再次弹出(无能量损失)算游戏成功。已知圆轨道半径为R,轨道DE的倾角θ=37°,滑块质量为m,滑块与轨道DE之间的动摩擦因数μ=0.5,其余都光滑,各轨道之间平滑连接;滑块可视为质点,弹射时从静止释放且弹簧的弹性势能完全转化为滑块动能,忽略空气阻力,sin37°=0.6,cos37°=0.8,重力加速度为g。
(1)若滑块第一次进入圆轨道,恰好能过最高点B,求滑块能滑上斜轨道的最大距离;
(2)若某次游戏弹射释放的弹性势能为Ep=5mgR,求滑块在斜轨道上通过的总路程;
(3)要使游戏成功(即滑块能返回弹射器、且只能返回一次),并要求滑块始终不脱离轨道,求弹射时弹性势能可能的范围。
【解答】解:(1)若滑块第一次进入圆轨道,恰好能过最高点B,则有:mg=mvB2R
解得:vB=gR
滑块从B点第一次运动到斜轨道最高点过程中,根据动能定理可得:﹣mg(2R﹣Lsinθ)﹣μmgLcosθ=0-12mvB2
解得:L=52R;
(2)若滑块恰好过B点,则弹簧弹性势能E1=2mgR+12mvB2
解得:E1=2.5mgR,因EP>E1,故滑块能过B点
设滑块第一次到斜轨道最高点时到D的距离为L1
由能量守恒定律可得:E1′=mgL1sinθ+μmgL1cosθ
得L1=5R
返回到C处时滑块的动能E1'=EP﹣2μmgL1cosθ=mgR
因此,此后滑块恰好不脱离轨道,在圆轨道与斜轨道间做往复运动,最终停在D点
全过程应用能量守恒定律可得:Ep=μmgscosθ
得s=12.5R;
(3)由题意可知,满足题意的弹性势能最小的条件为:滑块恰好第2次顺时针通过B
设第一次到斜轨道最高点时到D的距离为L2,根据动能定理可得:
mg(L2sinθ﹣2R)﹣μmgL2cosθ=12mvB2-0
得L2=12.5R
设第二次到斜轨道最高点时到D的距离为L2',根据动能定理可得:
mg(2R﹣L2'sinθ)﹣μmgL2'cosθ=0-12mvB2
得L2′=2.5R
两次在斜轨道往返后,滑块在C处具有的动能E2′=12mgR<mgR,满足题目要求
根据功能关系可得:Epmin=12mgR+2μmgcosθ(L2+L2')
解得:Epmin=12.5mgR
由题意可知,满足题意的弹性势能最大的条件为:滑块在斜轨道上往返两次后,恰能到达圆轨道上与圆心等高点处
分析计算可知第二次到斜轨道最高点到D的距离为L3'=5R
第一次到斜轨道最高点时离D距离为L3=25R
Epmx=mgR+2μmgcosθ(L3+L3')=25mgR
综上可得:12.5mgR≤EP≤25mgR。
答:(1)若滑块第一次进入圆轨道,恰好能过最高点B,滑块能滑上斜轨道的最大距离为52R;
(2)若某次游戏弹射释放的弹性势能为Ep=5mgR,滑块在斜轨道上通过的总路程为12.5R;
(3)要使游戏成功(即滑块能返回弹射器、且只能返回一次),并要求滑块始终不脱离轨道,弹射时弹性势能可能的范围为12.5mgR≤EP≤25mgR。
19.(2023•杭州二模)如图所示,某游戏装置由光滑平台、轨道AB、竖直圆管道BCDEC(管道口径远小于管道半径)、水平轨道CF、光滑直轨道FG平滑连接组成,B、C、C′为切点,A、F连接处小圆弧长度不计,A点上方挡片可使小滑块无能量损失地进入轨道AB。圆管道半径R=0.2m,管道中,内侧粗糙,外侧光滑。小滑块与轨道AB、CF的动摩擦因数均为μ=0.5,AB轨道长度l=0.4m,倾角θ=37°,CF长度L=2m,FG高度差h=0.8m,平台左侧固定一轻质弹簧,第一次压缩弹簧后释放小滑块,恰好可以运动到与管道圆心等高的D点,第二次压缩弹簧使弹性势能为0.36J时释放小滑块,小滑块运动到圆管道最高处E的速度为vE=1m/s,已知小滑块质量m=0.1kg可视为质点,sin37°=0.6,cos37°=0.8,不计空气阻力。求;
(1)第一次释放小滑块,小滑块首次到圆管上的C点时受到弹力大小;
(2)第二次释放小滑块,小滑块从C点运动到E点的过程,圆管道对滑块的摩擦力做的功;
(3)若第三次压缩弹簧使弹性势能为Ep时释放小滑块,要求小滑块在圆管道内运动时不受到摩擦力且全程不脱轨,最终停在C′F上。写出小滑块C′F上运动的总路程s与Ep之间的关系式,并指出Ep的取值范围。
【解答】解:(1)从C到D,对小滑块由动能定理可得
-mgR=0-12mvC2
解得
vC=2m/s
在C点由牛顿第二定律可得
FN-mg=mvC2R
联立解得
FN=3N
(2)从开始到E点由动能定理可得
Ep+mglsinθ-μmglcosθ-mgR(1+cosθ)+Wf=12mvE2-0
解得
Wf=﹣0.03J
(3)从开始到C,根据功能关系可得
EkC﹣Ep=mglsinθ﹣μmglcosθ+mgR(1﹣cosθ)
解得
EkC=Ep+0.12J
要能最终停在C′F上,必过E点,圆轨道运动无摩擦,所以
mg≤mvE2R
EkE=12mvE2≥0.1J
又有C到E,根据功能关系可得
﹣2mgR=EkE﹣EkC
解得
Ep≥0.38J
EkC≥0.5J
不从右侧斜面飞出需满足
EkC﹣μmgL﹣mgh≤0
解得
Ep≤1.68J
EkC≤1.8J
返回,若不过圆心等高处,可得
EkC﹣2μmgL﹣mgh≤0
解得
EkC≤2.2J
Ep≤2.08J
故
0.38J≤Ep≤1.68J
从开始到静止有
EkC﹣μmgs=0
则
s=(2Ep+0.24)m
其中
0.38J≤Ep≤1.68J
答:(1)第一次释放小滑块,小滑块首次到圆管上的C点时受到弹力大小3N;
(2)第二次释放小滑块,小滑块从C点运动到E点的过程,圆管道对滑块的摩擦力做的功﹣0.03J;
(3)小滑块C′F上运动的总路程s与Ep之间的关系式s=(2Ep+0.24)m;Ep的取值范围0.38J≤Ep≤1.68J。
20.(2021•浙江二模)如图1是组合玩具实物图,该玩具主要配件有小车、弹射器、三连环、滑跃板及部分直线轨道等。如图2为该玩具的轨道结构示意图,其中三连环是三个半径不同圆轨道Ⅰ、Ⅱ、Ⅲ组成,且轨道连接但不重叠。其圆心分别为O1、O2、O3,半径分别为R1=20cm、R2=15cm、R3=10cm,OA、AC为光滑水平轨道,滑跃板CD为足够长的粗糙倾斜轨道,轨道与水平面夹角θ可调(0≤θ<90o)。某次游戏中弹射器将小车自O点以一定初速度弹出,小车先后通过圆轨道Ⅰ、Ⅱ、Ⅲ后冲上滑跃板。小车可视为质点,其质量m=0.1kg,与滑跃板CD间动摩擦因数μ=33,其它阻力均不计,轨道各部分平滑连接,g取10m/s2。
(1)求小车通过圆轨道Ⅰ最高点B的最小速度vB;
(2)改变弹射器对小车的冲量,小车均能通过三连环,求小车通过圆轨道Ⅲ最低点A时受到轨道的支持力与弹射器对小车冲量的关系;
(3)若小车恰好能够通过三连环,为确保小车整个运动过程均不脱离轨道,分析滑跃板CD与水平面间夹角θ的取值范围。(可用三角函数表示)
【解答】解:(1)若能通过圆轨道O1最高点,
需满足:mg=mvB2R1
解得:vB=gR1=2m/s
(2)若能通过圆轨道O1最高点,则必能通过三连环。
根据机械能守恒可知小车运动至A点与被弹出时初速度相同,故有:vA=vO=Im
小车运动至圆轨道O3最低点A时,根据牛顿第二定律有:FN-mg=mvA2R3
解得:FN=100I2+1(N)
由(1)可得为确保小车通过三连环不脱离轨道,需满足:vB≥2m/s
根据动能定理有:-2mgR1=12mvB2-12mvO2
解得:vO≥10m/s,I≥1010N⋅s
故:轨道对小车作用力与弹射器对小车冲量的关系为:FN=100I2+1(N)(I≥1010N⋅s)
(3)由(1)可得小车恰好通过三连环则有:vB=2m/s
①当0≤θ≤30°时,满足mgsinθ≤μmgcosθ,小车冲上滑越板轨道CD后不再下滑,符合题目要求;
②假设小车自B点冲上滑越板轨道CD最大距离为L,根据动能定理有:2mgR1-mgLsinθ-μmgLcosθ=0-12mvB2
解得:L=0.5sinθ+μcosθ
在滑越板轨道CD上往返克服摩擦力做功:Wf=2μmgLcosθ=13tanθ+1
可知θ增大,Wf减小
若要不脱离轨道,返回三连环时不能超过圆轨道O3圆心等高位置,根据动能定理有:mg(2R1-R3)-Wf=0-12mvB2
解得:tanθ1=32
故当30°<θ≤arctan32时,小车往返运动最终静止于C点
综上所述当0≤θ≤arctan32时小车不脱离轨道。
答:(1)小车通过圆轨道Ⅰ最高点B的最小速度为2m/s
(2)小车通过圆轨道Ⅲ最低点A时受到轨道的支持力与弹射器对小车冲量的关系为:FN=100I2+1(N)(I≥1010N⋅s)
(3)当0≤θ≤arctan32时小车不脱离轨道。
21.(2023•浙江模拟)如图为某游戏装置的示意图。AB、CD均为四分之一圆弧,E为圆弧DEG的最高点,各圆弧轨道与直轨道相接处均相切。GH与水平夹角为θ=37°,底端H有一弹簧,A、O1、O2、D、O3、H在同一水平直线上。一质量为0.01kg的小钢球(其直径稍小于圆管内径,可视作质点)从距A点高为h处的O点静止释放,从A点沿切线进入轨道,B处有一装置,小钢球向右能无能量损失的通过,向左则不能通过且小钢球被吸在B点。若小钢球能够运动到H点,则被等速反弹。各圆轨道半径均为R=0.6m,BC长L=2m,水平直轨道BC和GH的动摩擦因数μ=0.5,其余轨道均光滑,小钢球通过各圆弧轨道与直轨道相接处均无能量损失。某次游戏时,小钢球从O点出发恰能第一次通过圆弧的最高点E。(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
(1)小钢球第一次经过C点时的速度大小vC;
(2)小钢球第一次经过圆弧轨道最低点B时对轨道的压力大小FB(保留两位小数);
(3)若改变小钢球的释放高度h,求出小钢球在斜面轨道上运动的总路程s与h的函数关系。
【解答】解:(1)小钢球从O点出发恰能第一次通过圆弧的最高点E,则小球到E点的速度为0,小球从C点到E点,根据动能定理得:
﹣mg•2R=0-12mvC2
代入数据解得:vC=26m/s
(2)从B点到C点,由动能定理得:﹣μmgL=12mvC2-12mvB2
小钢球经过B点,由牛顿第二定律得:N﹣mg=mvB2R
代入数据联立解得:N=56N≈0.83N
根据牛顿第三定律得,小钢球对轨道的压力大小FB=N=0.83N
(3)若小钢球恰能第一次通过E点,设小钢球释放点距A点为h1,从释放到E点,由动能定理得:
mg(h1﹣R)﹣μmgL=0
代入数据解得:h1=1.6m
若小钢球恰能第二次通过E点,设小球钢释放点距A点为h2,从释放到E点,由动能定理得:
mg(h1﹣R)﹣μmgL﹣2μmgcosθ•Rtanθ=0
代入数据解得:h2=2.24m
①若小球释放高度h<1.6m,无法到达E点,s=0
②若小球释放高度1.6m≤h<2.24m,小球能经过E点一次,μ<tanθ,则小钢球最终停在H点,从释放点到停在H点,根据动能定理得:
mgh﹣μmgL﹣μmgcosθ•s=0
代入数据解得:s=2.5(h﹣1)
③若小球释放高度2.24m≤h,小球经过E点两次,s=2Rtanθ=2×0.634m=1.6m
答:(1)小钢球第一次经过C点时的速度大小vC为26m/s;
(2)小钢球第一次经过圆弧轨道最低点B时对轨道的压力大小FB为0.83N;
(3)①若小球释放高度h<1.6m,s=0
②若小球释放高度1.6m≤h<2.24m,s=2.5(h﹣1)
③若小球释放高度2.24m≤h,s=1.6m。
22.(2022•浙江模拟)如图所示,倾斜轨道AB与水平直轨道BCDOMN在B处平滑连接,C、D间安装着水平传送带,C、D为两轮切点,间距L=6m,皮带轮半径r=0.1m;Q处安装着半径R=1m的竖直光滑圆轨道,在底部O处微微错开;N处安装着竖直弹性挡板。质量m=0.1kg的小滑块由A点以初速度v0=6m/s滑下,经传送带和圆轨道后与挡板相撞,撞后原速率弹回。滑块与传送带间的动摩擦因数μ1=0.2,与MN间的动摩擦因数为μ2=0.4,其余轨道均光滑。已知A点离地面高度h=1.5m,MN段的长度s=4.5m,g=10m/s2,滑块视为质点,空气阻力不计。
(1)若传送带静止,求滑块经过与圆心O等高的P点时对轨道的压力;
(2)若皮带轮以角速度ω1=20rad/s逆时针匀速转动,在滑块经过传送带的过程中,求滑块损失的机械能;
(3)若皮带轮以角速度ω2=90rad/s顺时针匀速转动,求滑块最后静止时离M点的距离;
(4)在皮带轮顺时针匀速转动的情况下,求滑块在MN段内滑行的总路程x与角速度ω的关系式
【解答】解:(1)物体从A到P,根据动能定理:mgh-μ1mgL-mgR=12mvP2-12mv02
解得vP=22m/s
在P点根据牛顿第二定律:FN=mvP2R=0.1×221N=2.2N
由牛顿第三定律可知:FN=F′N,F′N=2.2N
(2)若皮带轮以角速度ω1=20rad/s逆时针匀速转动时,摩擦力一直对滑块做负功,则损失的机械能
ΔE机=μ1mgL=0.2×0.1×10×6J=1.2J
(3)A到C机械能守恒:12mv02+mgh=12mvC2
得:vC=66m/s
皮带的线速度v=ωr2=9m/s>vC
设滑块加速至9m/s时,通过位移为x1
由12mv2-12mvC2=μ1mgx1,
得x1=1m<L=6m
所以,滑块先匀加速,后以v=9m/s匀速。即vD=vQ=9m/s
判断滑块能否过圆轨道最高点:
12mvQ2=4.05J>12m(gR)2+mg⋅2R=2.5J,所以能过最高点。
滑块第1次返回到M点时,剩余动能为Ek1,由Ek1-12mvQ2=-2μ2mgs
可得:Ek1=0.45J<mgR=1J;所以滑块只能在QN之间来回滑动,不会越过或脱离圆轨道。最终停在MN之间的某一位置。设滑块停止前在MN通过的总路程为x;
滑块由Q点至停下位置,动能定理:-12mvQ2=μ2mgx
可得:x=818m;MN段长s=4.5m
所以滑块停在离M点1.125m处。
(4)若滑块一直被传送带减速后,到达D点的速度为mgh-μ1mgL=12mv12-12mv02,解得v1=42m/s
若滑块一直被传送带加速后,到达D点的速度为mgh+μ1mgL=12mv'12-12mv02,解得v'1=90m/s
滑块要过圆轨道最高点时,需满足:12mv32≥12m(gR)2+mg⋅2R,所以,滑块到达D点的速度v3≥50m/s
综上所述,
当v带≤50m/s时,即ω≤1050rad/s时,滑块将脱离轨道,无法计算;
当50m/s≤v带≤90m/s时,即1050rad/s≤ω≤1090rad/s时
由12m(rω)2=μ2mgx,得x=ω2800
当v带≥90m/s时,即ω≥1090rad/s时
由12m(90)2=μ2mgx,得x=454m
答:(1)若传送带静止,滑块经过与圆心O等高的P点时对轨道的压力为2.2N;
(2)若皮带轮以角速度ω1=20rad/s逆时针匀速转动,在滑块经过传送带的过程中,滑块损失的机械能为1.2J;
(3)若皮带轮以角速度ω2=90rad/s顺时针匀速转动,滑块最后静止时离M点的距离为1.125m;
(4)在皮带轮顺时针匀速转动的情况下,
当v带≤50m/s时,即ω≤1050rad/s时,滑块将脱离轨道,无法计算;
当50m/s≤v带≤90m/s时,即1050rad/s≤ω≤1090rad/s时
由12m(rω)2=μ2mgx,得x=ω2800
当v带≥90m/s时,即ω≥1090rad/s时
由12m(90)2=μ2mgx,得x=454m
相关试卷
这是一份2021-2023年浙江省高考物理模拟试题分类——专题18电学实验,共66页。试卷主要包含了,其中α为金属丝的温度系数等内容,欢迎下载使用。
这是一份2021-2023年浙江省高考物理模拟试题分类——专题17力学实验,共61页。
这是一份2021-2023年浙江省高考物理模拟试题分类——专题10电磁感应,共52页。









