




所属成套资源:【高考模拟】2023届新高考数学复习系列模拟试卷(新高考数学)
专题2 《2023届新高考数学复习系列模拟试卷》(新高考II卷)1
展开
这是一份专题2 《2023届新高考数学复习系列模拟试卷》(新高考II卷)1,文件包含专题2《2023届新高考数学复习系列模拟试卷》新高考II卷1解析版docx、专题2《2023届新高考数学复习系列模拟试卷》新高考II卷1原卷版docx等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。
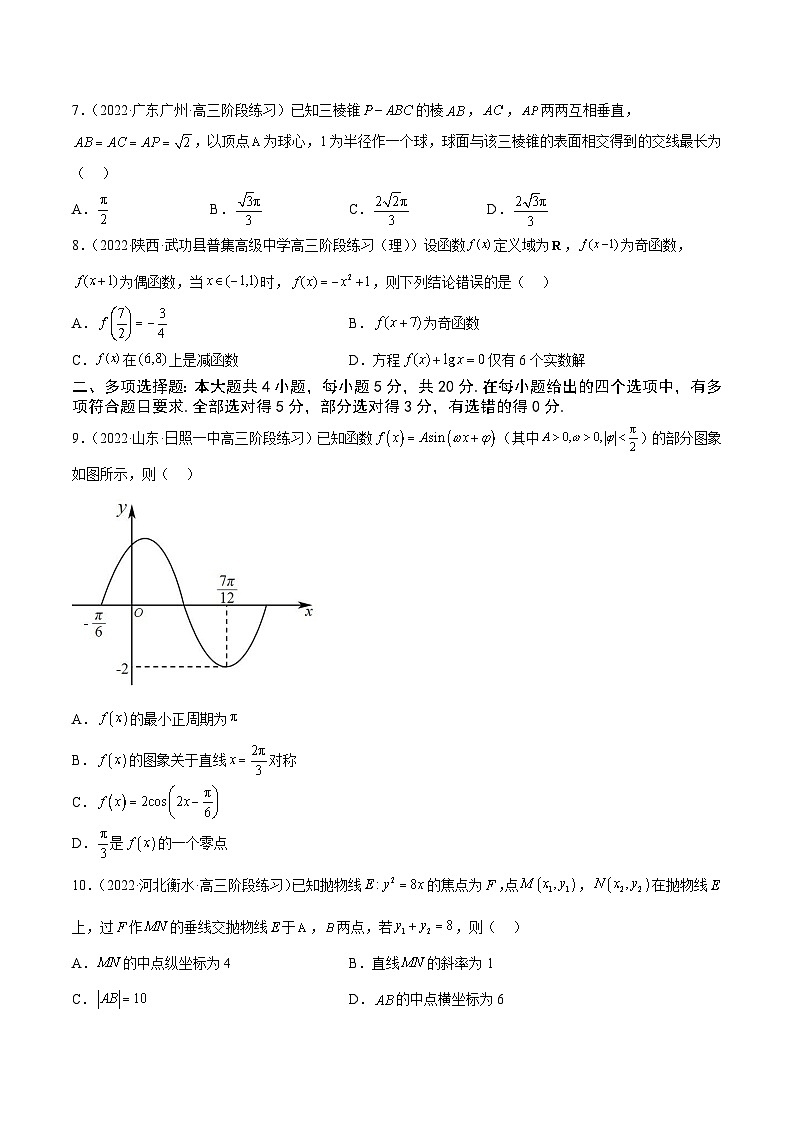
数 学 试 卷第I卷 选择题部分(共60分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2022·浙江邵外高三阶段练习)已知集合,,则等于( )A. B. C. D.【答案】A【分析】解不等式,求出,从而求出交集.【详解】,解得:,所以,因为,所以故选:A2.(2022·四川省绵阳南山中学高三阶段练习(文))已知的共轭复数为,则( )A. B. C. D.【答案】C【分析】使用共轭复数和复数乘法运算知识解决【详解】若,则,∴.故选:C.3.(2022·辽宁·沈阳市第四中学高三阶段练习)南宋数学家在《详解九章算法》和《算法通变本末》中提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,高阶等差数中前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列.现有高阶等差数列,其前7项分别为1,2,5,10,17,26,37,则该数列的第19项为( )A.290 B.325 C.362 D.399【答案】B【分析】先由条件判断该高阶等差数列为逐项差数之差成等差数列,进而得到,再利用累加法求得,进而可求得.【详解】设该数列为,则由,,,,…可知该数列逐项差数之差成等差数列,首项为1,公差为2,故,故,则,,,…,,上式相加,得,即,故.故选:B.4.(2022·全国·高三专题练习)已知为等边三角形,AB=2,设点P,Q满足,,,若,则=( )A. B.C. D.【答案】A【分析】设且先用表示出,,求出的值,即可求出.【详解】解:设且故选:A.5.(2022·上海海洋大学附属大团高级中学一模)电视台在电视剧开播前连续播放6个不同的广告,其中4个商业广告2个公益广告,现要求2个公益广告不能连续播放,则不同的播放方式共有( ).A. B.C. D.【答案】A【分析】由题意,利用插空法,可得答案.【详解】先排4个商业广告,则,即存在5个空,再排2个公益广告,则,故总排法:,故选:A.6.(2022·江苏南京·高三阶段练习)若,,则( )A. B.C. D.【答案】D【分析】先将切化弦,后用二倍角公式代入展开,解得,再根据平方关系结合的范围解得,最后将所求式子用和角公式展开并代值计算即可.【详解】由题,又 .故选:D.7.(2022·广东广州·高三阶段练习)已知三棱锥的棱,,两两互相垂直,,以顶点为球心,1为半径作一个球,球面与该三棱锥的表面相交得到的交线最长为( )A. B. C. D.【答案】D【分析】由条件可得球与三棱锥的表面的交线均为以点为顶点,半径为,圆心角为的圆弧,然后利用等体积法算出点到平面的距离,然后可得球与表面的交线为以的中心为圆心,半径为的圆,然后可得答案.【详解】因为三棱锥的棱,,两两互相垂直,,所以球与三棱锥的表面的交线均为以点为顶点,半径为,圆心角为的圆弧,其长度为,设点到平面的距离为,因为,所以是边长为的等边三角形,由可得,解得,所以球与表面的交线为以的中心为圆心,半径为的圆,其长度为,因为,所以以顶点为球心,1为半径作一个球,球面与该三棱锥的表面相交得到的交线最长为,故选:D8.(2022·陕西·武功县普集高级中学高三阶段练习(理))设函数定义域为,为奇函数,为偶函数,当时,,则下列结论错误的是( )A. B.为奇函数C.在上是减函数 D.方程仅有6个实数解【答案】C【分析】由题设可得关于、对称且周期为8,利用对称性和周期性求、判断奇偶性及在上的单调性,由与交点情况,数形结合判断根的个数.【详解】由题设,则关于对称,即,,则关于对称,即,所以,则,故,所以,即,故,所以的周期为8,,A正确;由周期性知:,故为奇函数,B正确;由题意,在与上单调性相同,而上递增,关于对称知:上递增,故上递增,所以在上是增函数,C错误;的根等价于与交点横坐标,根据、对数函数性质得:,,所以如下图示函数图象:函数共有6个交点,D正确. 故选:C二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对得5分,部分选对得3分,有选错的得0分.9.(2022·山东·日照一中高三阶段练习)已知函数(其中)的部分图象如图所示,则( )A.的最小正周期为B.的图象关于直线对称C.D.是的一个零点【答案】ACD【分析】结合函数图像求出的解析式,进而判断AC;利用代入检验法可判断BD.【详解】由图像可知,,,所以,即,故A正确;从而,由五点法可得,因为,所以,从而,故C正确;因为,所以不是的对称轴,故B错误;因为,所以是的一个零点,故D正确.故选:ACD.10.(2022·河北衡水·高三阶段练习)已知抛物线的焦点为,点,在抛物线上,过作的垂线交抛物线于,两点,若,则( )A.的中点纵坐标为4 B.直线的斜率为1C. D.的中点横坐标为6【答案】ABD【分析】根据中点坐标公式求得的中点纵坐标,判断A; 设直线方程,联立抛物线方程,利用根与系数的关系,可求得直线的斜率,判断B;利用抛物线弦长公式求得,判断C;根据根与系数的关系求得的中点横坐标,判断D.【详解】由题意得:点,在抛物线上,且,故,即的中点纵坐标为4,故A正确;由题意题可知当斜率不存在时,过作的垂线不会交抛物线于A,两点,故设直线方程为 ,联立,得: ,则,故B正确;由题意可设的方程为,联立,得: ,则,则,故C错误;的中点横坐标为 ,故D正确。故选:ABD11.(2022·湖南·高三开学考试)在正四棱台中,,,则( )A.该棱台的高为 B.该棱台的表面积为C.该棱台的体积为 D.该棱台外接球的表面积为【答案】ABD【分析】由题意可知,,则可求出正四棱台的高,斜高,即可求出其侧面积为,表面积,体积,设棱台外接球的球心到上底面的距离为,半径为,则可列出方程组,即可解出,则可求出外接球的表面积.【详解】由题可知,,所以正四棱台的高,故A正确,正四棱台的斜高,所以正四棱台的侧面积为,上、下底面的面积分别为4,16,即正四棱台的表面积,故B正确,正四棱台的体积,故C错误,设该棱台外接球的球心为,半径为,点到上底面的距离为,所以,解得,所以该棱台外接球的表面积为,故D正确.故选:ABD.12.(2022·辽宁·昌图县第一高级中学高三阶段练习)已知、,且,则下列不等式中一定成立的是( ).A. B. C. D. 【答案】ACD【分析】采用三角代换结合三角函数辅助角公式化简,可判断A;利用基本不等式判断B;利用基本不等式结合对数运算判断C; 利用基本不等式结合指数运算判断D.【详解】A选项,设 、 , ,∴ ,其中 且 ,∴ ,A正确;B选项,因为、,,故 ,即 ,当且仅当时取等号,B错,C选项, ,即 ,∴ ,当且仅当 时取等号(最大值),C正确,D选项,由B选项得,∴ ,当且仅当时取等号(最大值),D正确,故选:ACD.第II卷 非选择题部分(共90分)三、填空题:本大题共4小题,每小题5分,共20分.13.(2022·全国·高三专题练习)已知随机变量,则______.【答案】0.3【分析】正态曲线关于直线 ,即 对称,根据其对称性,即可求出答案.【详解】因为,,又所以,根据正态曲线的对称性,可知.故答案为:0.314.(2022·全国·高三专题练习(文))我国魏晋时期的科学家刘徽创立了“割圆术”,实施“以直代曲”的近似计算,用正边形进行“内外夹逼”的办法求出了圆周率的精度较高的近似值,这是我国最优秀的传统科学文化之一.借用“以直代曲”的近似计算方法,在切点附近,可以用函数图像的切线近似代替在切点附近的曲线来近似计算.设,则曲线在点处的切线方程为__________,用此结论计算__________.【答案】 【分析】本题首先可通过求导得出以及切线为,然后通过对数的运算得出,最后根据“以直代曲”即可得出结果.【详解】因为,,所以,,切线为,则,根据“以直代曲”,非常接近切点,则可以将代入切线近似代替,,故答案为:,.15.(2022·全国·高三专题练习)已知圆与直线交于,两点,点在直线上,且,则的取值范围为_____【答案】【分析】先联立直线与圆,得到两根之和,并由根的判别式求出的取值范围,求出中点坐标,从而求出的垂直平分线,利用得到是直线与的垂直平分线的交点,故联立两直线,求出交点横坐标,即,利用的取值范围,求出的取值范围.【详解】因为,所以是直线与的垂直平分线的交点,联立与,可得:,由得:或,设,则,所以,所以中点坐标为,的垂直平分线方程为:,与联立得:,因为或,所以故答案为:16.(2022·全国·高三专题练习)已知椭圆:的上顶点为B,右焦点为F,直线与椭圆交于两点,若椭圆的右焦点恰好为的垂心,则直线的方程为____________.【答案】.【分析】求出直线的斜率为,设出直线的方程为,与椭圆方程联立得到两根之和,两根之积,根据恰好为的垂心,故,列出方程,求出:或,经检验满足要求.【详解】易知,,直线的斜率为,从而直线的斜率为.设直线的方程为,,,由得.根据韦达定理,,,由于右焦点恰好为的垂心,故,于是 ,解之得:或.当时,点即为直线与椭圆的交点,不合题意;当时,经检验知和椭圆相交,符合题意.∴当且仅当直线的方程为时,点是的垂心.故答案为:四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(2022·江苏·赣榆智贤中学高三阶段练习)已知{an}是等差数列,a1=1,a4=10,且a1,ak(k∈N*),a6是等比数列{bn}的前3项.(1)求数列{an},{bn}的通项公式;(2)数列{cn}是由数列{an}的项删去数列{bn}的项后仍按照原来的顺序构成的新数列,求数列{cn}的前20项的和.【答案】(1)an=3n-2; bn=4n-1(2)767【分析】(1)根据等差数列基本量的计算即可求解公差,进而得通项,由等比中项可求解k=2,进而可求解公比,(2)将分组求和即可求解.(1)数列{an}是等差数列,设公差为d,且a1=1,a4=10.则解得d=3,所以an=1+3(n-1)=3n-2.又因为a1,ak,a6是等比数列{bn}的前3项,则=a1·a6,由于ak=3k-2,代入上式解得k=2.于是b1=1,b2=4,b3=16,因此等比数列{bn}的公比q=4,故数列{bn}的通项公式为bn=4n-1.(2)设数列{cn}的前20项的和为S20.因为b4=43=64=a22,b5=44=256=a86,,所以S20=(a1+a2+…+a24)-(b1+b2+b3+b4)=24×1+×3-(1+4+16+64)=767.18.(2022·广西·模拟预测(文))在中,角的对边分别为,已知(1)求;(2)若求的面积.【答案】(1)(2)【分析】(1)由已知,可将化简从而求得,然后再利用余弦二倍角公式直接求解即可;(2)由(1)问,可求解出,并判断为钝角,再根据,从而求解出,再使用和差公式计算,使用正弦定理求解出边长,然后带入面积公式即可完成求解.(1)由已知,,所以,因为,所以,此时,所以,得,所以;(2)由(1)可知,,所以且为钝角,由,可知,所以,由正弦定理可知,,所以,所以.19.(2022·重庆·高三阶段练习)中国男子篮球职业联赛(CBA)始于1995年,至今已有28个赛季,根据传统,在每个赛季总决赛之后,要举办一场南北对抗的全明星比赛,其中三分王的投球环节最为吸引眼球,三分王投球的比赛规则如下:一共有五个不同角度的三分点位,每个三分点位有5个球(前四个是普通球,最后一个球是花球),前四个球每投中一个得1分,投不中的得0分,最后一个花球投中得2分,投不中得0分.全明星参赛球员甲在第一个角度的三分点开始投球,已知球员甲投球的命中率为,且每次投篮是否命中相互独立.(1)记球员甲投完1个普通球的得分为X,求X的方差D(X);(2)若球员甲投完第一个三分点位的5个球后共得到了2分,求他是投中了花球而得到了2分的概率;(3)在比赛结束后与球迷的互动环节中,将球员甲在前两个三分点位使用过的10个篮球对应的小模型放入箱中,由幸运球迷从箱中随机摸出5个小模型,并规定,摸出一个花球小模型计2分,摸出一个普通球小模型计1分,求该幸运球迷摸出5个小模型后的总计分Y的数学期望.【答案】(1)(2)(3)6【分析】(1)用两点分布的概率公式计算即可.(2)设出事件,分别计算P(A)、P(AB),用条件概率公式计算得结果.(3)用超几何分布概率公式分别计算出所有可能情况的概率,再计算出数学期望.(1)由题设, 服从参数为 的两点分布, .(2)记 表示事件: “甲投完第一个三分点位的五个球得到了 2 分”; 记 表示事件: “甲投中花球”, 则于是 (3)由题设 值可取 , 则于是 20.(2022·湖北·荆州中学高三阶段练习)在斜三棱柱中,为等腰直角三角形,,侧面为菱形,且,点为棱的中点,,平面平面.(1)证明:平面平面;(2)求平面与平面的夹角的余弦值.【答案】(1)证明见解析(2)【分析】(1)结合已知条件,利用面面垂直的性质平面,然后利用面面垂直判定定理即可证明;(2)结合已知条件,首先证明平面,然后建立空间直角坐标系,并求出平面与平面的法向量,然后利用面面夹角的向量公式求解即可.(1)分别取,的中点和,连接,,,,如下图:因为,分别是,的中点,所以,且,因为点为棱的中点,所以,且,所以,且,所以四边形是平行四边形,所以.因为,是的中点,所以,又因为平面平面,且平面平面,所以平面,所以平面,因为平面,所以平面平面.(2)因为侧面为菱形,且,所以为正三角形,所以,由(1)知平面平面,平面平面,所以平面,又由,故,,两两垂直,设,则,以为坐标原点,,,分别为x,y,z轴的正方向,建立空间直角坐标系如下:则,,,,所以,,,设平面的法向量为,则,令,则,,从而.设平面的法向量为,则令,则,,从而,设平面与平面的夹角为,则,所以平面与平面的夹角的余弦值为.21.(2022·全国·模拟预测)已知双曲线的离心率为,左、右焦点分别为,,焦距为.点在第一象限的双曲线上,过点作双曲线切线与直线交于点.(1)证明:;(2)已知斜率为的直线与双曲线左支交于 两点,若直线,的斜率互为相反数,求的面积.【答案】(1)证明见解析;(2)【分析】(1)由题知双曲线的标准方程为,进而设设,在点的切线方程为,再与双曲线方程联立,结合位置关系得,进而得,再根据向量数量积的坐标表示证明即可;(2)设,直线的方程为,进而与双曲线方程联立,结合韦达定理与化简整理得,进而得,此时结合(1)得,,,再计算面积即可.(1)解:因为双曲线的离心率为,左、右焦点分别为,,焦距为,所以,,解得,所以,双曲线的标准方程为,因为过点作双曲线切线与直线交于点,故切线的斜率存在,所以,设,在点的切线方程为,联立方程得所以,,即①因为,代入①式得,解得所以,在点的切线方程为,所以点的坐标为,即,因为,所以所以,(2)解:由题,设直线的方程为,与双曲线方程联立得,设,所以因为直线,的斜率互为相反数,所以,所以,整理得:②将代入②整理得:③结合可知时,③式恒成立,所以,由(1)可知,,,所以,所以的面积.22.(2022·福建泉州·模拟预测)已知函数(1)讨论的单调性;(2)若在有两个极值点,求证:.【答案】(1)当时,在上单调递增;当或时,在上单调递减,在和上单调递增.(2)见解析【分析】(1)由题意,求导,根据含参二次函数的性质,由判别式进行分类讨论,可得答案;(2)由题意,根据极值点与导数零点的关系,结合韦达定理,化简不等式以及明确参数的取值范围,构造函数,求导研究新函数的单调性,可得答案.(1)由,求导得,易知恒成立,故看的正负,即由判别式进行判断,①当时,即,,则在上单调递增;②当时,即或,令时,解得或,当时,,则在上单调递减;当或,,则在和上单调递增;综上所述,当时,在上单调递增;当或时,在上单调递减,在和上单调递增.(2)在上由两个极值点,或,且为方程的两个根,即,,,,即,将,代入上式,可得:,由题意,需证,令,求导得,当时,,则在上单调递减,即,故.
相关试卷
这是一份专题12 《2023届新高考数学复习系列模拟试卷》(备战二模)(新高考II卷),文件包含专题12《2023届新高考数学复习系列模拟试卷》备战二模新高考II卷解析版docx、专题12《2023届新高考数学复习系列模拟试卷》备战二模新高考II卷原卷版docx等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。
这是一份专题10 《2023届新高考数学复习系列模拟试卷》(新高考II卷)5,文件包含专题10《2023届新高考数学复习系列模拟试卷》新高考II卷5解析版docx、专题10《2023届新高考数学复习系列模拟试卷》新高考II卷5原卷版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。
这是一份专题8 《2023届新高考数学复习系列模拟试卷》4(新高考II卷),文件包含专题8《2023届新高考数学复习系列模拟试卷》4新高考II卷解析版docx、专题8《2023届新高考数学复习系列模拟试卷》4新高考II卷原卷版docx等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。










