广东省深圳市宝安区松岗中学等六校2022-2023学年八年级下学期期中数学试卷 (含答案)

2022-2023学年广东省深圳市宝安区松岗中学等六校八年级（下）期中数学试卷

一、选择题（本题共有10小题，每小题3分，共30分，每小题有四个选项，其中只有一个正确的）

1．三角形的三边长分别为a、b、c，则下面四种情况中，不能判断此三角形为直角三角形的是（　　）

A．a＝3，b＝4，c＝5 B．a＝8，b＝15，c＝17 

C．a＝5，b＝12，c＝13 D．a＝12，b＝15，c＝18

2．不等式3+2x＜1的解集在数轴上表示正确的是 （　　）

A． B． 

C． D．

3．下列各式中，从左到右的变形是因式分解的是（　　）

A．15xy＝3x•5y B．2x2+2xy＝2x（x+y） 

C．x2+x+5＝x（x+1）+5 D．x2+2x+3＝（x+1）2+2

4．在下列不等式组中，无解的是（　　）

A． B． C． D．

5．在下列正多边形中，既是轴对称图形，又是中心对称图形的是（　　）

A． B． 

C． D．

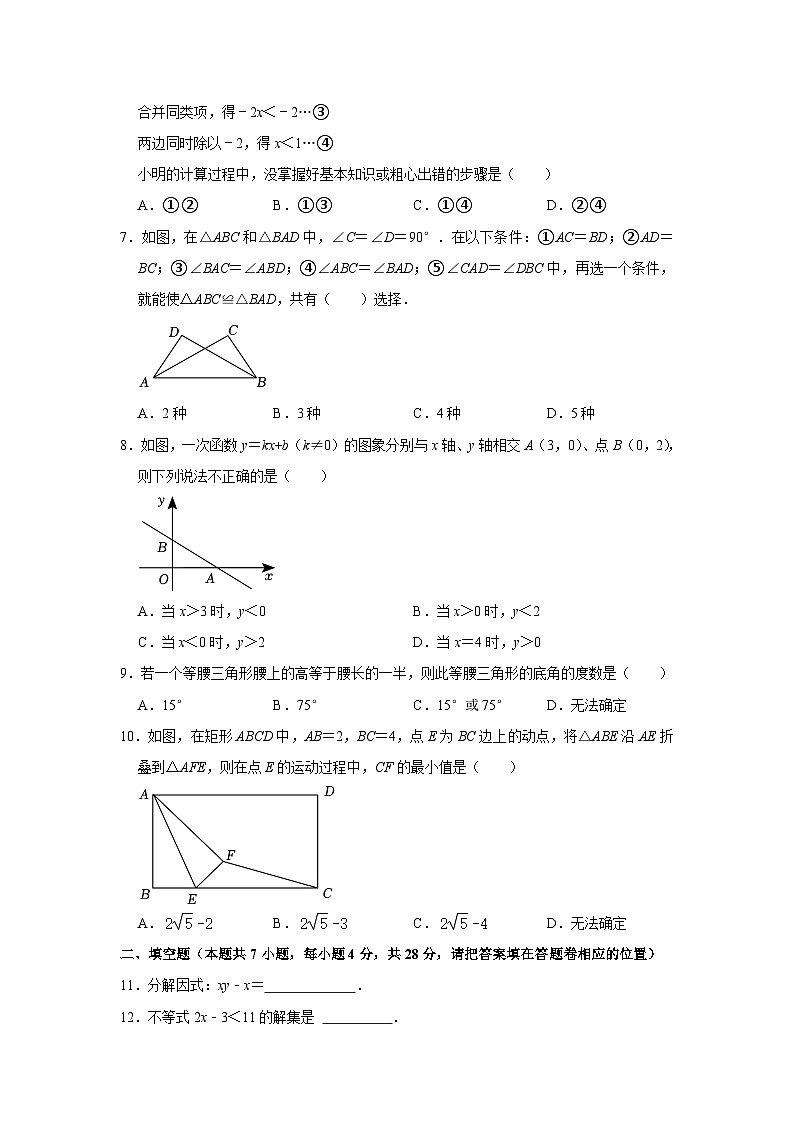
6．下面是小明解不等式的过程：

解：去分母，得x+5﹣1＜3x+2…①

移项，得x﹣3x＜2﹣5+1…②

合并同类项，得﹣2x＜﹣2…③

两边同时除以﹣2，得x＜1…④

小明的计算过程中，没掌握好基本知识或粗心出错的步骤是（　　）

A．①② B．①③ C．①④ D．②④

7．如图，在△ABC和△BAD中，∠C＝∠D＝90°．在以下条件：①AC＝BD；②AD＝BC；③∠BAC＝∠ABD；④∠ABC＝∠BAD；⑤∠CAD＝∠DBC中，再选一个条件，就能使△ABC≌△BAD，共有（　　）选择．

A．2种 B．3种 C．4种 D．5种

8．如图，一次函数y＝kx+b（k≠0）的图象分别与x轴、y轴相交A（3，0）、点B（0，2），则下列说法不正确的是（　　）

A．当x＞3时，y＜0 B．当x＞0时，y＜2 

C．当x＜0时，y＞2 D．当x＝4时，y＞0

9．若一个等腰三角形腰上的高等于腰长的一半，则此等腰三角形的底角的度数是（　　）

A．15° B．75° C．15°或75° D．无法确定

10．如图，在矩形ABCD中，AB＝2，BC＝4，点E为BC边上的动点，将△ABE沿AE折叠到△AFE，则在点E的运动过程中，CF的最小值是（　　）

A． B． C． D．无法确定

二、填空题（本题共7小题，每小题4分，共28分，请把答案填在答题卷相应的位置）

11．分解因式：xy﹣x＝　         　．

12．不等式2x﹣3＜11的解集是 　      　．

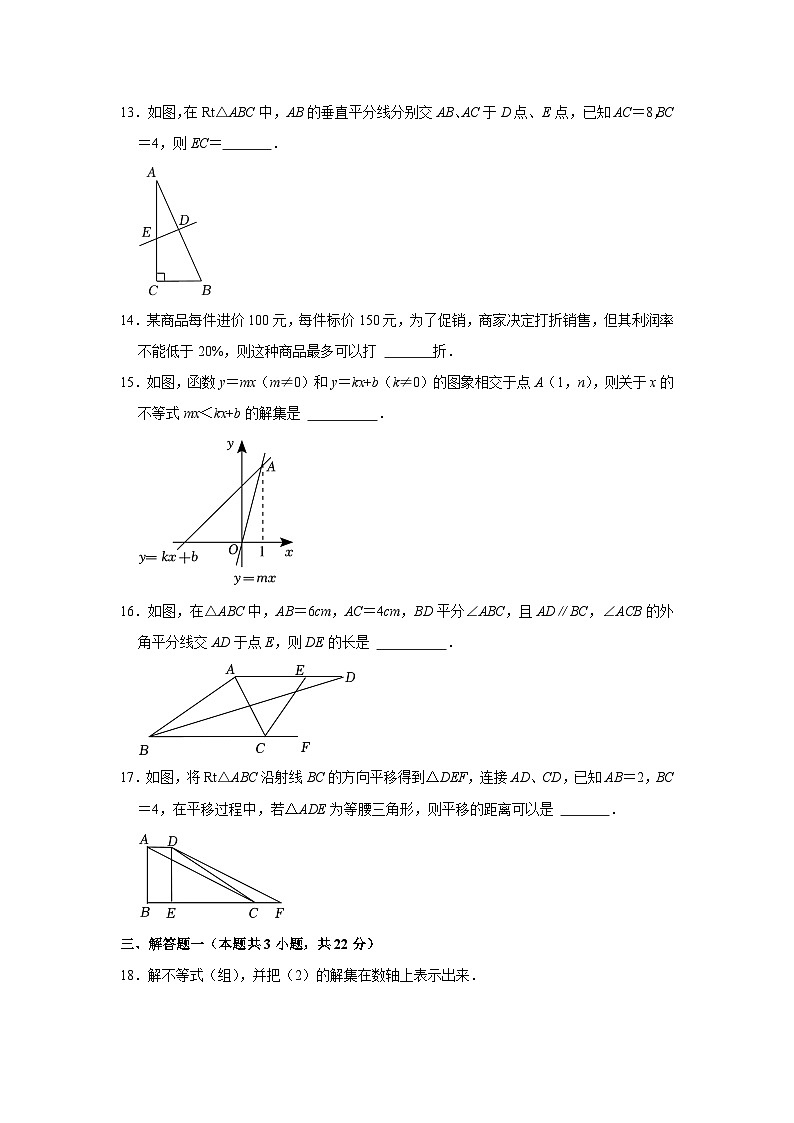
13．如图，在Rt△ABC中，AB的垂直平分线分别交AB、AC于D点、E点，已知AC＝8，BC＝4，则EC＝　   　．

14．某商品每件进价100元，每件标价150元，为了促销，商家决定打折销售，但其利润率不能低于20%，则这种商品最多可以打 　   　折．

15．如图，函数y＝mx（m≠0）和y＝kx+b（k≠0）的图象相交于点A（1，n），则关于x的不等式mx＜kx+b的解集是 　      　．

16．如图，在△ABC中，AB＝6cm，AC＝4cm，BD平分∠ABC，且AD∥BC，∠ACB的外角平分线交AD于点E，则DE的长是 　      　．

17．如图，将Rt△ABC沿射线BC的方向平移得到△DEF，连接AD、CD，已知AB＝2，BC＝4，在平移过程中，若△ADE为等腰三角形，则平移的距离可以是 　   　．

三、解答题一（本题共3小题，共22分）

18．解不等式（组），并把（2）的解集在数轴上表示出来．

（1）；

（2）．

19．学校准备用2000元购买名著和词典作为艺术节奖品，其中名著每套65元，词典每本40元，现已购买名著20套，问最多还能买词典多少本？

20．如图，△ABC为等边三角形，点D为BC边上一点，先将三角板60°角的顶点与D点重合，平放三角板，再绕点D转动三角板，三角板60°角的两边分别与边AB、AC交于点E、点F，当DE＝DF时，如图（2）所示．求证：△BDE≌△CFD．

四、解答题二（本题共3小题，共21分）

21．如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（﹣5，﹣2）、B（﹣4，﹣4）、C（﹣2，﹣1）．

（1）将△ABC先向右平移3个单位，再向上平移5个单位，得到△A1B1C1，请在原直角坐标系中画出△A1B1C1，并写出A1、B1、C1的坐标；

（2）若△A2B2C2与△A1B1C1关于原点O成中心对称，请写出A2、B2、C2的坐标，并在原直角坐标系中画出△A2B2C2．

22．学校开展篮球社团活动，需要购买若干个篮球，现从两家商场了解到同种篮球的标价均为100元/个，并且多买都有一定的优惠．甲商场的优惠条件是：前20个篮球按原价收费，其余优惠20%；乙商场的优惠条件是：全部打九折．

（1）设学校需要购买x个篮球，选择甲商场时，所需费用为y1元，选择乙商场时，所需费用为y2元，请分别写出y1、y2与x之间的关系式；

（2）若学校需要购买篮球数超过20个，选择到哪家商场购买，所需费用较少？

23．如图（1），点C、点D在直线l1上，点A、点B在直线l2上，且l1∥l2，连接AC、AD、BC、BD．

（1）请在图（1）中，找出三对面积相等的三角形：　                  　；

（2）利用（1）中的结论解决下面两个问题：

①将图（1）中的△ABC、△ABD进行以下操作：

第一步，分别复制△ABC、△ABD，粘贴，如图（2）所示的△A1B1C、△A2B2D．

第二步，先将图（2）中的△A1B1C、△A2B2D的顶点C、D重合，再将△A2B2D绕点C旋转到如图（3）所示位置．

若直线A2B2与A1B1相交于点E，连接CE．求证：CE平分∠A1EA2．

②如图（4），折线型小路P﹣M﹣Q，将四边形ABCD苗圃分成甲、乙两块，为了方便管理，要将折线型小路P﹣M﹣Q改为经过点P的直线型小路，使得甲、乙的面积前后不发生改变．请你在图（4）中画出直线型小路PN（不需要尺规作图，但要规范，并简单说明作图的关键步骤）．

五、解答题三（本题共2小题，共19分）

24．如图（1），已知CA＝CB，CD＝CE，且∠ACB＝∠DCE，将△DCE绕C点旋转（A、C、D三点在同一直线上除外）．

（1）求证：△ACD≌△BCE；

（2）在△DCE绕C点旋转的过程中，若ED、AB所在的直线交于点F，当点F为边AB的中点时，如图2所示．求证：∠ADF＝∠BEF（提示：利用类倍长中线方法添加辅助线）；

（3）在（2）的条件下，求证：AD⊥CD．

25．【问题背景】

在图（1）中，①～③的三个三角形，各自是由△ABC通过怎样的全等变换得到的？

​​​​【问题探究】

（1）我们发现：

Ⅰ：图（1）中，①号三角形能由△ABC通过一次轴对称得到，请在图（1）中画出对称轴．

Ⅱ：图（1）中，②号三角形能由△ABC通过一次平移得到，则平移的距离为 　   　单位．

Ⅲ：图（1）中，③号三角形能由△ABC通过先平移再旋转或先旋转再平移得到，请问：③号三角形能否由△ABC绕某个点，旋转一次得到？为解决这个问题，我们可以先解决两条相等的线段能否看成：一条线段是另一条线段绕某个点旋转一次得到．分析过程如下：

已知线段AB与线段CD相等，分两种情况讨论：当AB与CD对应时，如图（2），分别作AC与BD的中垂线交于点O1，连接O1A、O1C、O1B、O1D．

∵O1在AC的中垂线上

∴O1A＝O1C

同理，O1B＝O1D

又∵AB＝CD

∴△ABO1≌△CDO1（SSS）

∴∠AO1B＝∠CO1D

∴∠AO1C＝∠BO1D，即对应点与点O1形成的夹角相等

∴线段CD可以看成由线段AB绕点O1旋转一次得到.

第一种情况：

第二种情况：当AB与DC对应时，如图（3），同理可证．

综上所述：两条相等的线段可以看成：一条线段是另一条线段绕某个点旋转一次得到．

【问题解决】

（2）如图（4），已知△ABC≌△DEF（且满足△DEF不能由△ABC通过平移得到）．现在来解决△DEF能由△ABC绕某个点通过一次旋转得到的问题：

①通过尺规作图找到旋转中心O；

②证明：△DEF能由△ABC绕点O通过一次旋转得到．（提示：只要证明关键的对应点到点O的距离相等和关键的对应点与点O形成的夹角相等）

2022-2023学年第二学期期中学情调查试卷答案

 八年级  数学

第一部分  （选择题，共30分）

一、选择题

1.D    2.A    3.B    4.D    5.B

6.C    7.C    8.D    9.C    10.A

第二部分  （非选择题，共90分）

二、填空题

11.         12.       13.3

14. 八       15.         16.2cm         17.

三、解答题一（本题共3小题，共22分）

18.（本题共2小题，每小题5分，共10分）解不等式（组），并把（2）的解集在数轴上表示出来：

（1）                （2）

19.（本题6分）

建议：①设未知数时，不能出现“最多”两字，否则，扣1分。

②此题用算术方法解题：正确，给4分；不正确，不给分.

20.（本题6分）

证明：∵△ABC为等边三角形

      ∴∠B＝∠C＝60°…………………………………1分

      ∵∠BDF＝∠CFD+∠C，   ∠EDF＝60°

      ∴∠BDE＝∠CFD……………………….……………..3

      在△BDE和△CFD中

∴△BDE≌△CFD（AAS）……………………….6分

四、解答题二（本题共3小题，共21分）

21.（本题6分）

解：

（1）A1（－2,3）； B1（－1，1）；C1（1，4）………………………2分

（2）A2（2,－3）； B2（1，－1）；C2（－1，－4）……………………4分

                                  ………………………………6分

建议：在（1）（2）中，每小问写对1到2个，给1分，全对给2分；

      画图对一个给1分，对两个给2分

22.（本题7分）

解：

（1）

（2）

23.（本题8分）

解：（1）△ABD和△ABC；△ACD和△BCD；△AOD和△BOC；……………..3分

   （2）如图（3），作CG⊥A1B1于点G、作CH⊥A2B2于点H.

       ∵S      ＝S               A1B1 ＝A2B2

        ∴CG＝ CH

        ∴CE平分∠A1 E A2.         ……………..6分

   （3）作图如图（4）所示. ……………..7分

       ①连接PQ；   ②作MN∥PQ；   ③连接PN，PN即为所求. …………….8分

       建议：关键步骤只要有MN∥PQ就可不扣分.

五、解答题三（本题共2小题，共19分）

24.（本题9分）

解（1）∵∠ACB＝∠DCE

     ∴∠ACD＝∠BCE

       在△ACD和△BCE中

∴△ACD≌△BCE（SAS）……………………….3分

  （2）延长EF到G，使得FG=FD，连接BG.

       ∵F为AB的中点

       ∴AF＝BF

         在△ADF和△BGF中

∴△ADF≌△BGF（SAS）……………………….5分

 ∴ AD＝BG    ∠ADF＝∠G   

     由（1）可知：AD＝BE

    ∴BG＝BE

    ∴∠G＝∠BEF

∴∠ADF＝∠BEF     ……………………….6分

（3）∵CD＝CE

∴∠CDE＝∠CED

∴∠CDE＋∠ADF＝∠CED＋∠BEF＝∠CEB

由（1）可知：∠ADC＝∠CEB

  ∴∠CDE＋∠ADF＝∠ADC

    ∵∠CDE＋∠ADF＋∠ADC＝180°

 ∴∠ADC＝90°

∴AD⊥CD……………………….9分

25.（本题10分）

解：

（1）Ⅰ：如图所示………………………1分

Ⅱ：平移的距离为    8    单位………………………2分

（2）①图中点O即为所求的作的旋转中心. ………………………6分

②∵点O为AD的中垂线和BE的中垂线的交点

∴OA＝OD，OB＝OE

∵△ABC≌△DEF

      ∴AB＝DE,  BC＝EF,  ∠ABC＝∠DEF

         在△OAB和△ODE中

∴△OAB≌△ODE（SSS）. ………………………8分

∴∠1＝∠2      ∠AOB＝∠DOE

∴∠OBC＝∠OEF     ∠AOD＝∠BOE

在△OBC和△OEF中

∴△OBC≌△OEF（SAS）

∴OC＝OF，  ∠BOC＝∠EOF

∴  ∠COF＝∠BOE            . ………………………10分

综上所述：[1]对应点与旋转中心形成的夹角相等

 ∠COF＝∠BOE＝∠AOD

[2]对应点到旋转中心的距离相等

 OA＝OD，OB＝OE，OC＝OF

建议：证到了以上结论，没写总结，不扣分