2022-2023年人教版(2019)新教材高中物理必修2 第8章机械能守恒定律第3节动能和动能定理(1)课件

这是一份2022-2023年人教版(2019)新教材高中物理必修2 第8章机械能守恒定律第3节动能和动能定理(1)课件，共17页。

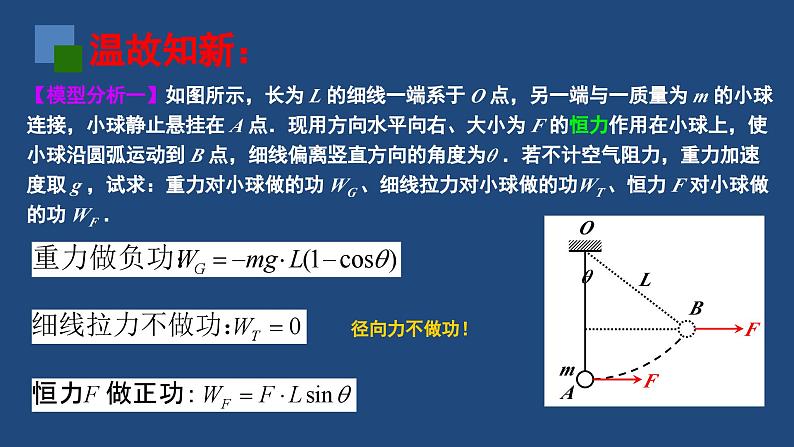
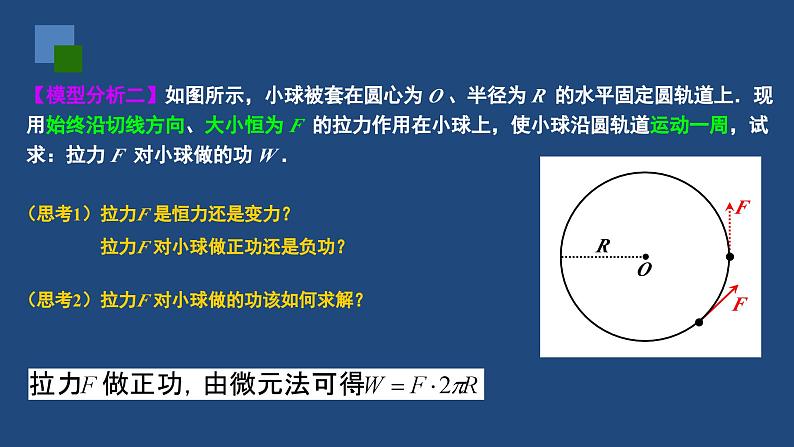
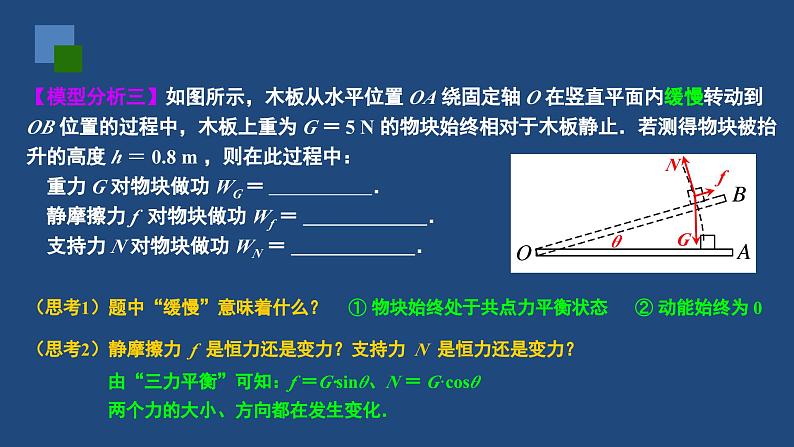
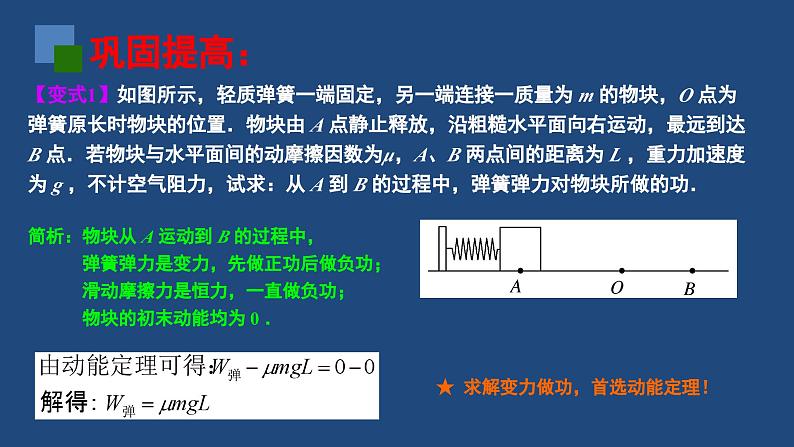
动能和动能定理（变力做功问题）温故知新：【模型分析一】如图所示，长为 L 的细线一端系于 O 点，另一端与一质量为 m 的小球连接，小球静止悬挂在 A 点．现用方向水平向右、大小为 F 的恒力作用在小球上，使小球沿圆弧运动到 B 点，细线偏离竖直方向的角度为θ ．若不计空气阻力，重力加速度取 g ，试求：重力对小球做的功 WG 、细线拉力对小球做的功WT 、恒力 F 对小球做的功 WF ．径向力不做功！【模型分析二】如图所示，小球被套在圆心为 O 、半径为 R 的水平固定圆轨道上．现用始终沿切线方向、大小恒为 F 的拉力作用在小球上，使小球沿圆轨道运动一周，试求：拉力 F 对小球做的功 W ．（思考1）拉力F 是恒力还是变力？ 拉力F 对小球做正功还是负功？（思考2）拉力F 对小球做的功该如何求解？【模型分析三】如图所示，木板从水平位置 OA 绕固定轴 O 在竖直平面内缓慢转动到 OB 位置的过程中，木板上重为 G ＝ 5 N 的物块始终相对于木板静止．若测得物块被抬升的高度 h ＝ 0.8 m ，则在此过程中： 重力 G 对物块做功 WG ＝ ． 静摩擦力 f 对物块做功 Wf ＝ ． 支持力 N 对物块做功 WN ＝ ．（思考1）题中“缓慢”意味着什么？① 物块始终处于共点力平衡状态 ② 动能始终为 0（思考2）静摩擦力 f 是恒力还是变力？支持力 N 是恒力还是变力？由“三力平衡”可知：f ＝G·sinθ、N ＝ G·cosθ两个力的大小、方向都在发生变化．（思考3）物块缓慢运动的路径是圆弧： 静摩擦力 f 始终是径向力，因而 Wf ＝ 0 ． 支持力 N 始终是切向力，能否用“微元法”求解 WN ？不能用“微元法”求解 WN ，因为：① 圆弧长度无法计算 ② N 的大小在变化（思考4）能否尝试用“动能定理”求解 WN ？求解恒力做功，首选 W＝F·x ，但须关注力和位移的对应关系．微元法可以“化曲为直、化变力为恒力”，是一种分析理解变力做功的好方法！求解变力做功的方法有很多，动能定理是最常用的一种，值得优先考虑！典例分析：【例题1】如图所示，某同学将一静置于草坪上的足球沿水平方向用力踢出，足球获得的初速度为 v0＝20 m/s ，沿草坪向前滚动的最大距离约为 75 m ．若足球质量 m ＝0.4 kg ，试求： （1）该同学踢球时所做的功 W1 ． （2）足球沿草坪运动过程中，阻力对足球做的功 W2 ．（思考1）该同学踢球时，脚对球的作用力是恒力还是变力？ 这个力对球做正功还是做负功？ 怎样用动能定理求解？（思考2）足球沿草坪运动过程中，所受的阻力是恒力还是变力？ 这个力对球做正功还是做负功？ 怎样用动能定理求解？【变式1】如图所示，轻质弹簧一端固定，另一端连接一质量为 m 的物块，O 点为弹簧原长时物块的位置．物块由 A 点静止释放，沿粗糙水平面向右运动，最远到达 B 点．若物块与水平面间的动摩擦因数为μ，A、B 两点间的距离为 L ，重力加速度为 g ，不计空气阻力，试求：从 A 到 B 的过程中，弹簧弹力对物块所做的功．巩固提高：简析：物块从 A 运动到 B 的过程中， 弹簧弹力是变力，先做正功后做负功； 滑动摩擦力是恒力，一直做负功； 物块的初末动能均为 0 ．★ 求解变力做功，首选动能定理！典例分析：【例题2】如图所示，质量 m＝0.1 kg 的小球从距水平面 h＝2 m 的斜面轨道上由静止释放，经水平轨道 AB 后进入一半径 R ＝0.4 m 的竖直半圆形轨道 BCD ，并恰能通过最高点 D ．已知所有轨道都不光滑，小球经过轨道连接点处均无能量损耗，不计空气阻力，重力加速度 g＝10 m/s2，试求：小球从 A 运动到 D 的过程中，克服摩擦力所做的功 ．简析：从小球运动的全过程看，摩擦力是变力，且始 终做负功；小球初动能为 0 ，但末动能未知．（思考1）怎样才能求得小球的末动能（或末速度大小）？“恰能通过”意味着什么？（思考2）如何用动能定理求解小球克服摩擦力所做的功？★ 圆周运动中利用向心力方程求速度★ 注意向心力方程、动能定理方程的书写规范！【变式2】如图所示，由细管道拼接成的竖直轨道，其圆形部分半径分别为 R 和 0.5R ，A、B 均为圆形轨道的最高点．一质量为 m 的小球通过这段轨道时，在 A 点时刚好对管壁无压力，在 B 点时对管外侧壁压力大小为 0.5mg ．若不计空气阻力，试求：由 A 点运动到 B 点的过程中，小球克服摩擦力所做的功 ． 巩固提高：★ 向心力方程、动能定理方程的书写规范！【例题3】一辆汽车质量为 m ，发动机的额定功率为 P ．某时刻，该汽车从静止开始沿平直公路启动加速，经时间 t0 后达到最高速度 vm ．若该汽车在整个加速过程中，发动机功率始终保持为 P ，所受阻力大小恒为 f ，试求：该汽车在时间 t0 内经过的位移大小．典例分析：（思考1）汽车在时间 t0 内的位移能否用运动学公式求解？不能用运动学公式求解，因为汽车恒功率启动加速过程中，发动机的牵引力逐渐减小，因而做的是加速度越来越小的变加速直线运动．（思考3）尝试一下用动能定理求解这段位移 x ？（思考2）汽车做变加速运动的位移 x ，应该和哪个力做功有直接关系？发动机牵引力做正功，是变力功，只能用 Pt0 来表示．阻力做负功，是恒力功，可以用 －f·x 来表示．★ 动能定理还可以用来求解“非匀变速直线运动”的位移，不失为一种巧妙的方法！课堂小结：1．求解变力做功，动能定理是最常用的方法．当物体受到一个变力和几个恒力 共同作用时，可以先求出几个恒力所做的功，然后用动能定理间接求变力做 的功，即W恒＋W变＝ΔEk .2．动能定理常与平抛运动、圆周运动相结合，解决这类问题要特别注意： （1）与平抛运动相结合时，要注意应用运动的合成与分解的方法，如分解 位移或分解速度求平抛运动的有关物理量． （2）与竖直平面内的圆周运动相结合时，应特别注意最高点的向心力条件． 课后作业：【练习1】如图所示，长为 L 的细线一端系于 O 点，另一端与一质量为 m 的小球连接，小球静止悬挂在 A 点．现用方向水平向右、大小未知的拉力 F 作用在小球上，使小球沿圆弧缓慢运动到 B 点，细线偏离竖直方向的角度为θ ．若不计空气阻力，重力加速度取 g ，试求：拉力 F 对小球做的功 WF ．OABLFFθm【练习2】如图所示，某同学从 h ＝5 m 高处，以初速度 v0＝8 m/s 沿水平方向抛出一个质量为 m ＝0.5 kg 的橡皮球，测得橡皮球落地前瞬间的速度为 v ＝12 m/s ．若重力加速度 g ＝10 m/s2 ，试求： （1）该同学抛球时所做的功． （2）橡皮球在空中运动时克服空气阻力做的功．【练习3】如图所示，质量 m＝0.1 kg 的小球被固接在长为 L＝0.5 m 的轻杆的一端，轻杆可绕另一端 O 在竖直平面内转动，最初小球静止在最低点 A ．现给小球提供一水平向右的初速度 v0 ，并测得此时轻杆对小球的拉力大小为 F＝8.2 N．若小球绕行半周后恰能到达最高点 B ，重力加速度 g＝10 m/s2，不考虑轻杆所受的任何阻力，试求： （1）初速度 v0 的大小． （2）从 A 运动到 B 的过程中，空气阻力 对小球做的功 W ．