单元复习02 圆与方程【过知识】- 2022-2023学年高二数学单元复习（苏教版2019选择性必修第一册）

展开

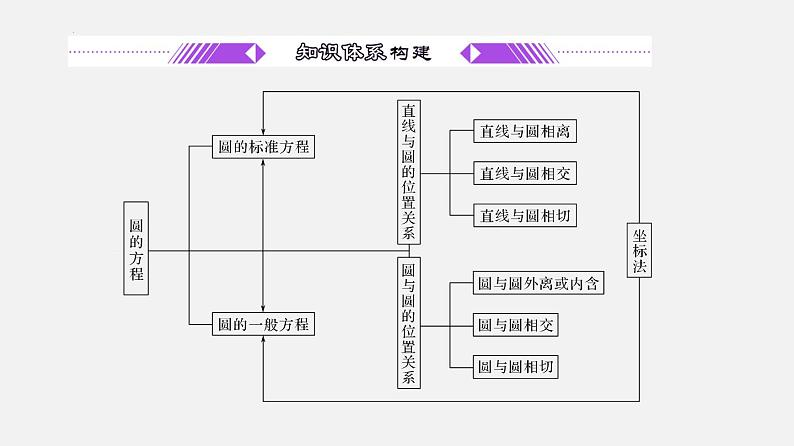
这是一份单元复习02 圆与方程【过知识】- 2022-2023学年高二数学单元复习（苏教版2019选择性必修第一册），共60页。

考点1 圆的方程
2.点与圆的位置关系(1)根据点到圆心的距离d与圆的半径r的大小判断:d>r⇔点在圆外;d=r⇔点在圆上;dr2⇔点在圆外;(x0-a)2+(y0-b)2=r2⇔点在圆上;(x0-a)2+(y0-b)2 考点2 直线与圆的位置关系
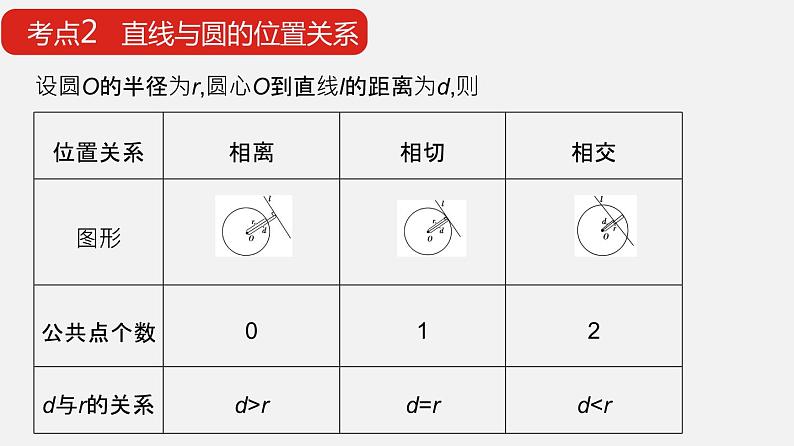
设圆O的半径为r,圆心O到直线l的距离为d,则
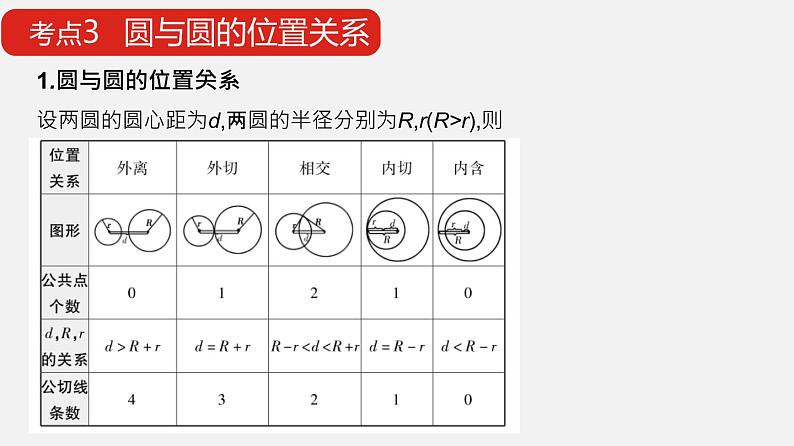
考点3 圆与圆的位置关系
1.圆与圆的位置关系设两圆的圆心距为d,两圆的半径分别为R,r(R>r),则
易错警示判断圆与圆位置关系的注意点对于圆与圆的位置关系,从交点的个数,也就是两圆方程联立组成的方程组的解的组数来判断的话,有时得不到确切的结论.如当Δ<0时,需要再根据图形判断两圆是外离,还是内含;当Δ=0时,还需要判断两圆是外切,还是内切.
2.两圆相交时,公共弦所在直线的方程设圆C1:x2+y2+D1x+E1y+F1=0　①,圆C2:x2+y2+D2x+E2y+F2=0　②,若两圆相交,则有一条公共弦,由①-②,得(D1-D2)x+(E1-E2)y+F1-F2=0　③.方程③表示圆C1与圆C2的公共弦所在直线的方程.
注意 (1)方程③存在的前提是两圆相交;(2)两圆公共弦的垂直平分线过两圆的圆心;(3)求公共弦长时,几何法比代数法简单且易求.
题组一　走出误区1．判断下列结论是否正确(请在括号中打“√”或“×”)(1)确定圆的几何要素是圆心与半径．(　　)(2)已知点A(x1，y1)，B(x2，y2)，则以AB为直径的圆的方程是(x－x1) (x－x2)＋(y－y1)(y－y2)＝0．(　　)
题组二　走进教材2．圆C的圆心在x轴上，并且过点A(－1,1)和B(1,3)，则圆C的方程为_________________．
(x－2)2＋y2＝10　
3．以点(2，－1)为圆心且与直线3x－4y＋5＝0相切的圆的方程为(　　)A．(x－2)2＋(y＋1)2＝3B．(x＋2)2＋(y－1)2＝3C．(x－2)2＋(y＋1)2＝9D．(x＋2)2＋(y－1)2＝9
题组三　走向高考4．(2019·北京高考)设抛物线y2＝4x的焦点为F，准线为l．则以F为圆心，且与l相切的圆的方程为________________．[解析]　∵抛物线的方程为y2＝4x，∴其焦点坐标为F(1,0)，准线l的方程为x＝－1．又∵圆与直线l相切，∴圆的半径r＝2，故圆的方程为(x－1)2＋y2＝4．
(x－1)2＋y2＝4　
　　　　(1)(2021·海南海口二中模拟)已知圆M与直线3x－4y＝0及3x－4y＋10＝0都相切，圆心在直线y＝－x－4上，则圆M的方程为(　　)A．(x＋3)2＋(y－1)2＝1B．(x－3)2＋(y＋1)2＝1C．(x＋3)2＋(y＋1)2＝1D．(x－3)2＋(y－1)2＝1(2)(2021·重庆一中、湖北鄂州期中)圆C半径为2，圆心在x轴的正半轴上，直线3x＋4y＋4＝0与圆C相切，则圆C的方程为(　　)A．x2＋y2－2x－3＝0B．x2＋y2－4x＝0C．x2＋y2＋4x＝0D．x2＋y2＋2x－3＝0
x2＋y2－2x＝0　
(x－2)2＋y2＝9　
求圆的方程的两种方法(1)直接法：根据圆的几何性质，直接求出圆心坐标和半径，进而写出方程．(2)待定系数法：①若已知条件与圆心(a，b)和半径r有关，则设圆的标准方程，依据已知条件列出关于a，b，r的方程组，进而求出a，b，r的值；②若已知条件没有明确给出圆心或半径，则选择圆的一般方程，依据已知条件列出关于D，E，F的方程组，进而求出D，E，F的值．
〔变式训练1〕(1)若圆C的半径为1，圆心在第一象限，且与直线4x－3y＝0和x轴都相切，则该圆的标准方程是(　　)A．(x－2)2＋(y－1)2＝1B．(x－2)2＋(y＋1)2＝1C．(x＋2)2＋(y－1)2＝1D．(x－3)2＋(y－1)2＝1(2)圆心在直线x－2y－3＝0上，且过点A(2，－3)，B(－2，－5)的圆的方程为______________________．
(x＋1)2＋(y＋2)2＝10　
[引申]本例中若P(x，y)，则(1)(x＋3)2＋(y＋1)2的最大值为______，最小值为_____．(2)|x－2y－2|的取值范围为______________________．
(3)形如(x－a)2＋(y－b)2形式的最值问题，可转化为动点到定点的距离的平方的最值问题．(4)圆上的点到定点(定直线)距离的最大值与最小值为圆心到定点(定直线)距离与半径的和与差．
　　　　已知圆x2＋y2＝4上一定点A(2,0)，B(1,1)为圆内一点，P、Q为圆上的动点．(1)求线段AP中点的轨迹方程；(2)若∠PBQ＝90°，求线段PQ中点的轨迹方程．[解析]　(1)设AP的中点为M(x，y)，由中点坐标公式可知，P点坐标为(2x－2,2y)．因为P点在圆x2＋y2＝4上，所以(2x－2)2＋(2y)2＝4．故线段AP中点的轨迹方程为(x－1)2＋y2＝1．
(2)设PQ的中点为N(x，y)．在Rt△PBQ中，|PN|＝|BN|，设O为坐标原点，连接ON，则ON⊥PQ，所以|OP|2＝|ON|2＋|PN|2＝|ON|2＋|BN|2，所以x2＋y2＋(x－1)2＋(y－1)2＝4．故线段PQ中点的轨迹方程为x2＋y2－x－y－1＝0．
考法1 直线与圆的位置关系
示例1 直线l :mx-y+1-m=0与圆C:x2+(y-1)2=5的位置关系是 A.相交　　　B.相切　　　C.相离　　　D.不确定
考法探究与圆有关的位置关系
解法三(点与圆的位置关系法)　直线l:mx-y+1-m=0过定点(1,1),因为点(1,1)在圆x2+(y-1)2=5的内部,所以直线l与圆相交.答案 A点评判断直线与圆的位置关系时,通常利用圆心到直线的距离,注意求距离时直线方程必须化成一般式.
方法技巧判断直线与圆的位置关系的方法(1)几何法:由圆心到直线的距离d与半径r的大小关系来判断.(2)代数法:联立直线与圆的方程,消元后得到关于x(或y)的一元二次方程,根据一元二次方程的解的个数(也就是方程组解的个数)来判断.①如果Δ<0,那么直线与圆相离;②如果Δ=0,那么直线与圆相切;③如果Δ>0,那么直线与圆相交.
(3)点与圆的位置关系法:若直线过定点且该定点在圆内,则可判断直线与圆相交.注意直线与圆的位置关系的判断方法中,若直线和圆的方程已知或圆心到直线的距离易表达,则用几何法较简单;若直线或圆的方程中含有参数,且圆心到直线的距离不易表达,则用代数法较简单.
考法2 圆与圆的位置关系
示例2 分别求当实数k为何值时,圆C1:x2+y2+4x-6y+12=0与圆C2:x2+y2-2x-14y+k=0相交和相切.思维导引
方法技巧圆与圆的位置关系的判断方法(1)几何法:由两圆的圆心距d与半径R,r(R>r)的关系来判断.d>R+r⇔外离;d=R+r⇔外切;R-r注意判断圆与圆的位置关系时,一般不用代数法,因为利用代数法不能判断内切或外切,内含或外离;利用几何法的关键是判断圆心距|C1C2|与R+r,R-r的关系.
考法3 圆的弦长问题
考法4 圆的切线问题
(2) ∵(3-1)2+(1-2)2=5>4,∴点M在圆C 外部.当过点M的直线斜率不存在时,直线方程为x=3,即x-3=0.又点C(1,2)到直线x-3=0的距离d=3-1=2=r,即此时满足题意,所以直线x=3是圆的切线;当切线的斜率存在时,设切线方程为y-1=k(x-3),即kx-y+1-3k=0,
2.求过圆外一点(x0,y0)的切线方程的方法
思维拓展与圆的切线有关的结论(1)过圆x2+y2=r2上一点P(x0,y0)的切线方程为x0x+y0y=r2;(2)过圆(x-a)2+(y-b)2=r2上一点P(x0,y0)的切线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2;(3)过圆x2+y2=r2外一点P(x0,y0)作圆的两条切线,切点分别为A,B,则切点弦AB所在直线的方程为x0x+y0y=r2;(4)过圆C:(x-a)2+(y-b)2=r2(r>0)外一点P(x0,y0)作圆C的两条切线,切点分别为A,B,则切点弦AB所在直线的方程为(x0-a)(x-a)+(y0-b)(y-b)=r2;

相关试卷更多