中考数学一轮复习知识梳理课件第5章《四边形》课时23 (含答案)

这是一份中考数学一轮复习知识梳理课件第5章《四边形》课时23 (含答案)，共42页。PPT课件主要包含了cm2，拓展提升等内容，欢迎下载使用。
1. 如图1-5-23-1，菱形ABCD中，E，F分别是AB，AC的中点.若EF=3，则菱形ABCD的周长是 (　　)A. 12 B. 16 C. 20 D. 242. 矩形具有而菱形不具有的性质是 (　　)A. 两组对边分别平行且相等B. 两组对角分别相等C. 相邻两角互补D. 对角线相等
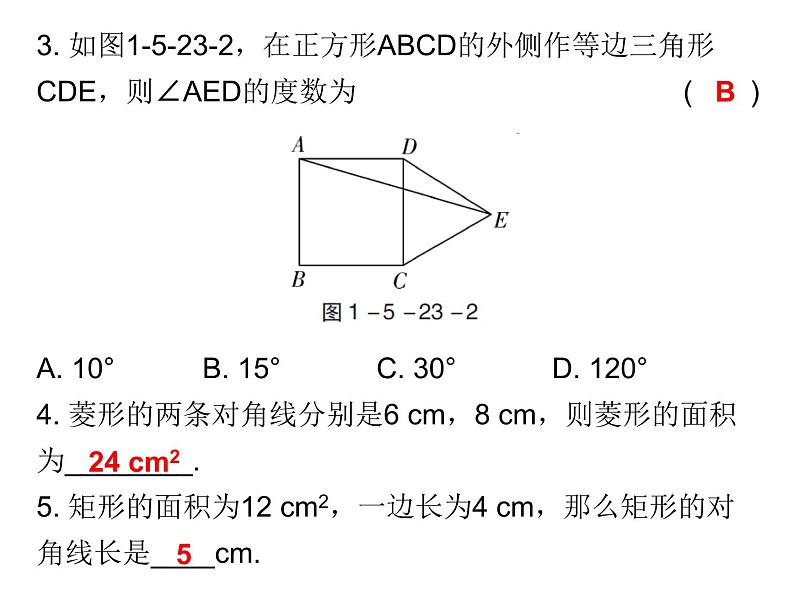
3. 如图1-5-23-2，在正方形ABCD的外侧作等边三角形CDE，则∠AED的度数为 (　　)A. 10° B. 15° C. 30° D. 120°4. 菱形的两条对角线分别是6 cm，8 cm，则菱形的面积为________. 5. 矩形的面积为12 cm2，一边长为4 cm，那么矩形的对角线长是____cm.
1. 特殊平行四边形的判定和性质：
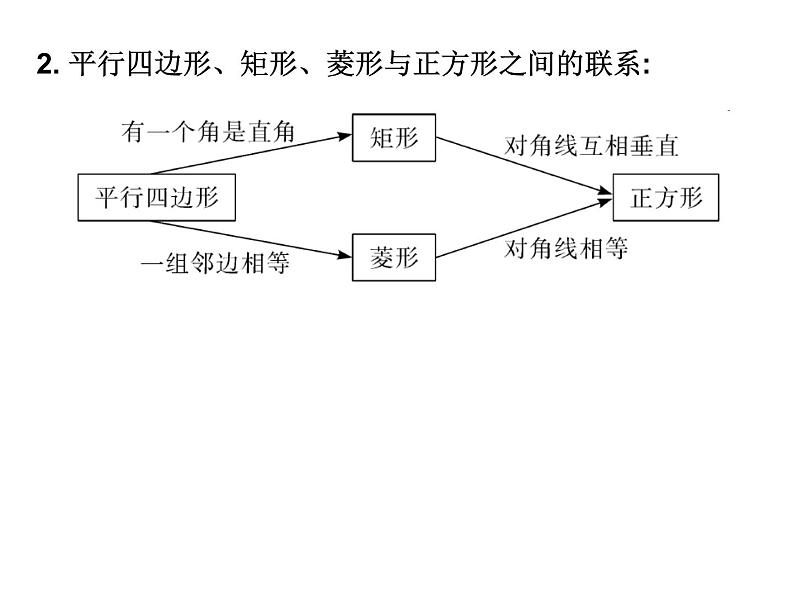
2. 平行四边形、矩形、菱形与正方形之间的联系:
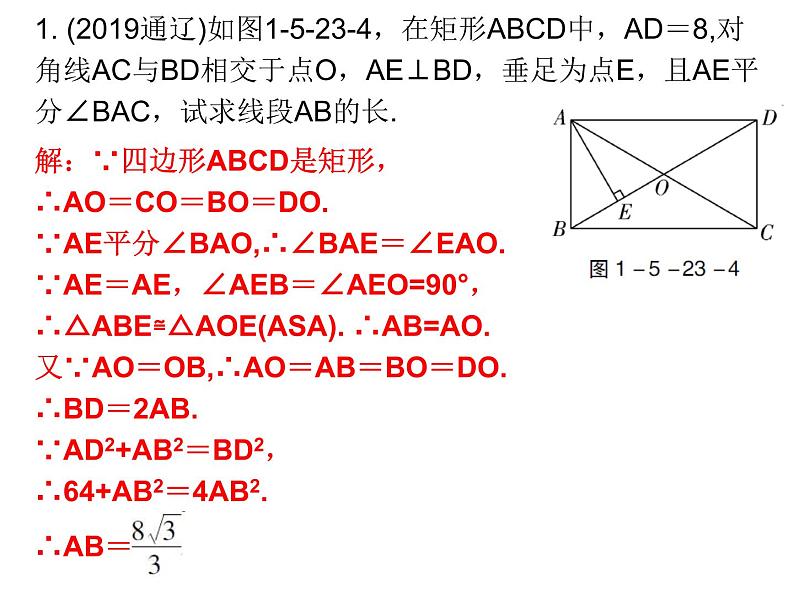
1. (2019通辽)如图1-5-23-4，在矩形ABCD中，AD＝8,对角线AC与BD相交于点O，AE⊥BD，垂足为点E，且AE平分∠BAC，试求线段AB的长.
3. (2019新疆)如图1-5-23-6，在菱形ABCD中，对角线AC, BD相交于点O，E是CD的中点，连接OE. 过点C作CF∥BD交OE的延长线于点F，连接DF. 求证：(1)△ODE≌△FCE；(2)四边形OCFD是矩形.
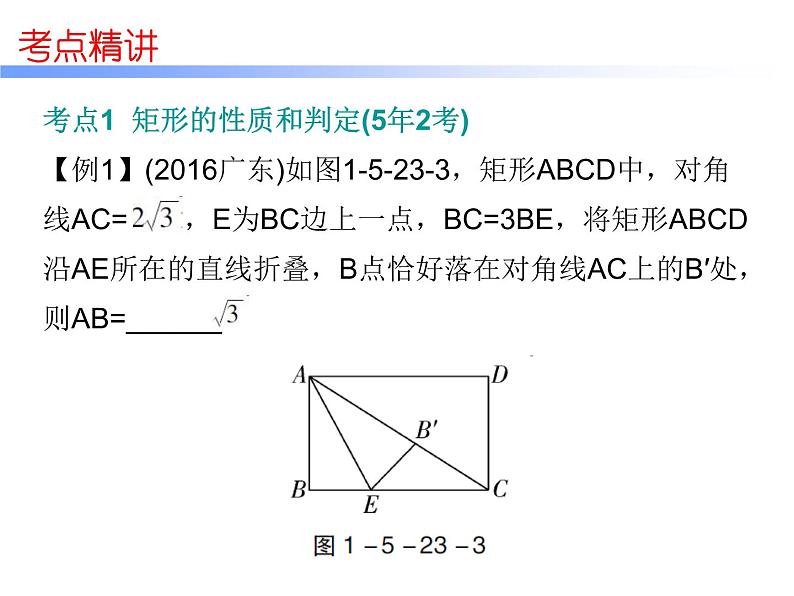
考点点拨： 本考点的题型不固定，难度中等. 解此类题的关键在于熟练掌握矩形的性质和判定定理.
考点2 菱形的性质和判定(5年2考)【例2】 (2015广东)如图1-5-23-7，菱形ABCD的边长为6，∠ABC=60°，则对角线AC的长是______.
1. (2017广东)如图1-5-23-8，已知四边形ABCD，四边形ADEF都是菱形，∠BAD=∠FAD，∠BAD为锐角. (1)求证：AD⊥BF；(2)若BF=BC，求∠ADC的度数.
2. (2019泸州)一个菱形的边长为6，面积为28，则该菱形的两条对角线的长度之和为 (　　)A. 8 B. 12 C. 16 D. 32
3. (2019百色)如图1-5-23-9，菱形ABCD中，作BE⊥AD, CF⊥AB，分别交AD,AB的延长线于点E,F. (1)求证：AE＝BF；(2)若点E恰好是AD的中点，AB＝2，求BD的值.
(1)证明：∵四边形ABCD是菱形,∴AB＝BC，AD∥BC.∴∠A＝∠CBF.∵BE⊥AD,CF⊥AB，∴∠AEB＝∠BFC＝90°.∴△AEB≌△BFC(AAS).∴AE＝BF.(2)解：∵E是AD的中点，且BE⊥AD,∴直线BE为AD的垂直平分线.∴BD＝AB＝2.
考点点拨： 本考点的题型不固定，难度中等. 解此类题的关键在于熟练掌握菱形的性质和判定定理.
考点3 正方形的性质和判定(5年2考)【例3】(2019广东)如图1-5-23-10，正方形ABCD的边长为4，延长CB至点E使EB＝2，以EB为边在上方作正方形EFGB，延长FG交DC于点M，连接AM，AF，H为AD的中点，连接FH分别与AB，AM交于点N，K，则下列结论：①△ANH≌△GNF；②∠AFN＝∠HFG；③FN＝2NK；④S△AFN∶S△ADM＝1∶4. 其中正确的结论有 (　　)A. 1个B. 2个C. 3个D. 4个
2. (2017广东)如图1-5-23-12，已知正方形ABCD，点E是BC边的中点，DE与AC相交于点F，连接BF.下列结论：①S△ABF=S△ADF；②S△CDF=4S△CEF；③S△ADF=2S△CEF；④S△ADF=2S△CDF，其中正确的是 (　　) A. ①③ B. ②③ C. ①④ D. ②④
3. (2019长沙)如图1-5-23-13，正方形ABCD中，点E，F分别在AD，CD上，且DE＝CF，AF与BE相交于点G. (1)求证：BE＝AF；(2)若AB＝4，DE＝1，求AG的长.
考点点拨： 本考点的题型不固定，难度中等. 解此类题的关键在于熟练掌握正方形的性质和判定定理.
5. (2019徐州)如图1-5-23-17，矩形ABCD中，AC,BD交于点O，M,N分别为BC,OC的中点. 若MN＝4，则AC的长为______.
7. (2019宁波)如图1-5-23-19，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F，H在菱形ABCD的对角线BD上. (1)求证：BG=DE；(2)若E为AD的中点，FH=2，求菱形ABCD的周长.
(1)证明：∵四边形EFGH是矩形，∴EH=FG，EH∥FG.∴∠GFH=∠EHF.∵∠BFG=180°-∠GFH，∠DHE=180°-∠EHF，∴∠BFG=∠DHE.∵四边形ABCD是菱形，∴AD∥BC.∴∠GBF=∠EDH.∴△BGF≌△DEH(AAS).∴BG=DE.
(2)解：连接EG，如答图1-5-23-2.∵四边形ABCD是菱形，∴AD=BC，AD∥BC.∵E为AD的中点，∴AE=ED.∵BG=DE，∴AE=BG，AE∥BG.∴四边形ABGE是平行四边形.∴AB=EG.∵EG=FH=2，∴AB=2.∴菱形ABCD的周长为4×2=8.
8. (2019青岛)如图1-5-23-20，在菱形ABCD中，点P是BC边上一点，连接AP，点E，F是AP上的两点，连接DE，BF，使得∠AED=∠ABC，∠ABF=∠BPF. 求证：(1)△ABF≌△DAE；(2)DE=BF+EF.
证明：(1)∵四边形ABCD是菱形，∴AB=AD，AD∥BC.∴∠BPA=∠DAE.∵∠ABC=∠AED，∴∠BAF=∠ADE.∵∠ABF=∠BPF，∠BPA=∠DAE，∴∠ABF=∠DAE.∵AB=DA，∴△ABF≌△DAE(ASA).(2)∵△ABF≌△DAE，∴AE=BF，DE=AF.∵AF=AE+EF=BF+EF，∴DE=BF+EF.
9. (2019孝感)如图1-5-23-21，正方形ABCD中，点E,F分别在边CD，AD上，BE与CF交于点G. 若BC＝4，DE＝AF＝1，求GF的长.