江苏省苏州市5年（2018-2022）中考数学真题分类汇编-07解答题（基础题）知识点分类

这是一份江苏省苏州市5年（2018-2022）中考数学真题分类汇编-07解答题（基础题）知识点分类，共23页。试卷主要包含了计算，先化简，再求值，解不等式组，问题1等内容，欢迎下载使用。

江苏省苏州市5年（2018-2022）中考数学真题分类汇编-07解答题（基础题）知识点分类
一．实数的运算（共1小题）
1．计算：|﹣|+﹣（）2．
二．代数式求值（共1小题）
2．已知3x2﹣2x﹣3＝0，求（x﹣1）2+x（x+）的值．
三．分式的化简求值（共1小题）
3．先化简，再求值：÷（1﹣），其中，x＝﹣3．
四．解一元一次不等式组（共1小题）
4．解不等式组：
五．一次函数的应用（共1小题）
5．某商店代理销售一种水果，六月份的销售利润y（元）与销售量x（kg）之间函数关系的图象如图中折线所示．请你根据图象及这种水果的相关销售记录提供的信息，解答下列问题：
（1）截止到6月9日，该商店销售这种水果一共获利多少元？
（2）求图象中线段BC所在直线对应的函数表达式．
日期
销售记录
6月1日
库存600kg，成本价8元/kg，售价10元/kg（除了促销降价，其他时间售价保持不变）．
6月9日
从6月1日至今，一共售出200kg．
6月10、11日
这两天以成本价促销，之后售价恢复到10元/kg．
6月12日
补充进货200kg，成本价8.5元/kg．
6月30日
800kg水果全部售完，一共获利1200元．

六．反比例函数图象上点的坐标特征（共2小题）
6．如图，在平面直角坐标系中，四边形OABC为矩形，点C，A分别在x轴和y轴的正半轴上，点D为AB的中点．已知实数k≠0，一次函数y＝﹣3x+k的图象经过点C、D，反比例函数y＝（x＞0）的图象经过点B，求k的值．

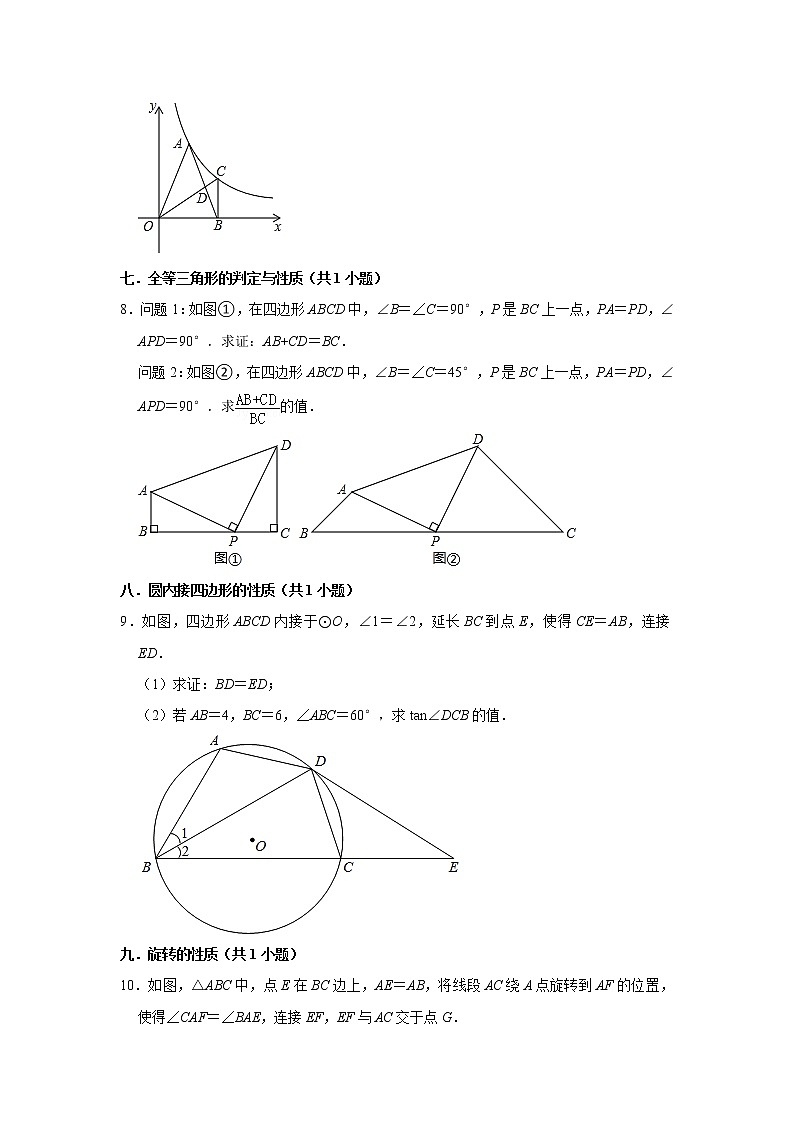
7．如图，A为反比例函数y＝（其中x＞0）图象上的一点，在x轴正半轴上有一点B，OB＝4．连接OA，AB，且OA＝AB＝2．
（1）求k的值；
（2）过点B作BC⊥OB，交反比例函数y＝（其中x＞0）的图象于点C，连接OC交AB于点D，求的值．

七．全等三角形的判定与性质（共1小题）
8．问题1：如图①，在四边形ABCD中，∠B＝∠C＝90°，P是BC上一点，PA＝PD，∠APD＝90°．求证：AB+CD＝BC．
问题2：如图②，在四边形ABCD中，∠B＝∠C＝45°，P是BC上一点，PA＝PD，∠APD＝90°．求的值．

八．圆内接四边形的性质（共1小题）
9．如图，四边形ABCD内接于⊙O，∠1＝∠2，延长BC到点E，使得CE＝AB，连接ED．
（1）求证：BD＝ED；
（2）若AB＝4，BC＝6，∠ABC＝60°，求tan∠DCB的值．

九．旋转的性质（共1小题）
10．如图，△ABC中，点E在BC边上，AE＝AB，将线段AC绕A点旋转到AF的位置，使得∠CAF＝∠BAE，连接EF，EF与AC交于点G．
（1）求证：EF＝BC；
（2）若∠ABC＝65°，∠ACB＝28°，求∠FGC的度数．

一十．相似三角形的判定与性质（共1小题）
11．如图，在矩形ABCD中，E是BC的中点，DF⊥AE，垂足为F．
（1）求证：△ABE∽△DFA；
（2）若AB＝6，BC＝4，求DF的长．

一十一．用样本估计总体（共1小题）
12．某校九年级640名学生在“信息素养提升”培训前、后各参加了一次水平相同的测试，并以同一标准折算成“6分”、“7分”、“8分”、“9分”、“10分”5个成绩．为了解培训效果，用抽样调查的方式从中抽取了32名学生的2次测试成绩，并用划记法制成了如表表格：
训前
成绩（分）
6
7
8
9
10
划记
正正

正
正

人数（人）
12
4
7
5
4
培训后
成绩（分）
6
7
8
9
10
划记

一

正
正正正
人数（人）
4
1
3
9
15
（1）这32名学生2次测试成绩中，培训前测试成绩的中位数是m，培训后测试成绩的中位数是n，则m　 　n；（填“＞”、“＜”或“＝”）
（2）这32名学生经过培训，测试成绩为“6分”的百分比比培训前减少了多少？
（3）估计该校九年级640名学生经过培训，测试成绩为“10分”的学生增加了多少人？
一十二．条形统计图（共2小题）
13．某学校计划在八年级开设“折扇”、“刺绣”、“剪纸”、“陶艺”四门校本课程，要求每人必须参加，并且只能选择其中一门课程，为了解学生对这四门课程的选择情况，学校从八年级全体学生中随机抽取部分学生进行问卷调查，并根据调查结果绘制成如图所示的条形统计图和扇形统计图（部分信息未给出）．

请你根据以上信息解决下列问题：
（1）参加问卷调查的学生人数为 　 　名，补全条形统计图（画图并标注相应数据）；
（2）在扇形统计图中，选择“陶艺”课程的学生占 　 　%；
（3）若该校八年级一共有1000名学生，试估计选择“刺绣”课程的学生有多少名？
14．某学校计划在“阳光体育”活动课程中开设乒乓球、羽毛球、篮球、足球四个体育活动项目供学生选择．为了估计全校学生对这四个活动项目的选择情况，体育老师从全体学生中随机抽取了部分学生进行调查（规定每人必须并且只能选择其中的一个项目），并把调查结果绘制成如图所示的不完整的条形统计图和扇形统计图，请你根据图中信息解答下列问题：

（1）求参加这次调查的学生人数，并补全条形统计图；
（2）求扇形统计图中“篮球”项目所对应扇形的圆心角度数；
（3）若该校共有600名学生，试估计该校选择“足球”项目的学生有多少人？
一十三．列表法与树状图法（共2小题）
15．一只不透明的袋子中装有1个白球，3个红球，这些球除颜色外都相同．
（1）搅匀后从中任意摸出1个球，这个球是白球的概率为 　 　；
（2）搅匀后从中任意摸出1个球，记录颜色后放回，搅匀，再从中任意摸出1个球，求2次摸到的球恰好是1个白球和1个红球的概率．（请用画树状图或列表等方法说明理由）
16．在一个不透明的布袋中装有三个小球，小球上分别标有数字0、1、2，它们除数字外都相同．小明先从布袋中任意摸出一个小球，记下数字作为平面直角坐标系内点A的横坐标，将此球放回、搅匀，再从布袋中任意摸出一个小球，记下数字作为平面直角坐标系内点A的纵坐标．请用树状图或表格列出点A所有可能的坐标，并求出点A在坐标轴上的概率．
一十四．游戏公平性（共1小题）
17．4张相同的卡片上分别写有数字0、1、﹣2、3，将卡片的背面朝上，洗匀后从中任意抽取1张，将卡片上的数字记录下来；再从余下的3张卡片中任意抽取1张，同样将卡片上的数字记录下来．
（1）第一次抽取的卡片上数字是负数的概率为 　 　；
（2）小敏设计了如下游戏规则：当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时，甲获胜；否则，乙获胜．小敏设计的游戏规则公平吗？为什么？（请用树状图或列表等方法说明理由）

江苏省苏州市5年（2018-2022）中考数学真题分类汇编-07解答题（基础题）知识点分类
参考答案与试题解析
一．实数的运算（共1小题）
1．计算：|﹣|+﹣（）2．
【分析】根据二次根式的运算法则即可求出答案．
【解答】解：原式＝+3﹣＝3
【点评】本题考查实数的运算，解题的关键是熟练运用运算法则，本题属于基础题型．
二．代数式求值（共1小题）
2．已知3x2﹣2x﹣3＝0，求（x﹣1）2+x（x+）的值．
【分析】直接利用整式的混合运算法则化简，进而合并同类项，再结合已知代入得出答案．
【解答】解：原式＝x2﹣2x+1+x2+x
＝2x2﹣x+1，
∵3x2﹣2x﹣3＝0，
∴x2﹣x＝1，
∴原式＝2（x2﹣x）+1
＝2×1+1
＝3．
【点评】此题主要考查了代数式求值，正确将原式变形是解题关键．
三．分式的化简求值（共1小题）
3．先化简，再求值：÷（1﹣），其中，x＝﹣3．
【分析】先根据分式的混合运算顺序和运算法则化简原式，再将x的值代入计算可得．
【解答】解：原式＝÷（﹣）
＝÷
＝•
＝，
当x＝﹣3时，
原式＝＝＝．
【点评】本题主要考查分式的化简求值，解题的关键是掌握分式的混合运算顺序和运算法则．
四．解一元一次不等式组（共1小题）
4．解不等式组：
【分析】分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．
【解答】解：解不等式x+1＜5，得：x＜4，
解不等式2（x+4）＞3x+7，得：x＜1，
则不等式组的解集为x＜1．
【点评】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
五．一次函数的应用（共1小题）
5．某商店代理销售一种水果，六月份的销售利润y（元）与销售量x（kg）之间函数关系的图象如图中折线所示．请你根据图象及这种水果的相关销售记录提供的信息，解答下列问题：
（1）截止到6月9日，该商店销售这种水果一共获利多少元？
（2）求图象中线段BC所在直线对应的函数表达式．
日期
销售记录
6月1日
库存600kg，成本价8元/kg，售价10元/kg（除了促销降价，其他时间售价保持不变）．
6月9日
从6月1日至今，一共售出200kg．
6月10、11日
这两天以成本价促销，之后售价恢复到10元/kg．
6月12日
补充进货200kg，成本价8.5元/kg．
6月30日
800kg水果全部售完，一共获利1200元．

【分析】（1）由表格信息可知，从6月1日到6月9日，成本价8元/kg，售价10元/kg，一共售出200kg，根据利润＝每千克的利润×销售量列式计算即可；
（2）设B点坐标为（a，400），根据题意列方程求出点B的坐标，设线段BC所在直线对应的函数表达式为y＝kx+b，利用待定系数法解答即可．
【解答】解：（1）200×（10﹣8）＝400（元）
答：截止到6月9日，该商店销售这种水果一共获利400元；

（2）设点B坐标为（a，400），根据题意得：
（10﹣8）×[600﹣（a﹣200）]+（10﹣8.5）×200＝1200，
解这个方程，得a＝350，
∴点B坐标为（350，400），
设线段BC所在直线对应的函数表达式为y＝kx+b（k≠0），则：
，解得，
∴线段BC所在直线对应的函数表达式为．
【点评】本题考查一次函数的应用，解答本题的关键是明确题意，求出相应的函数解析式，利用一次函数的性质解答．
六．反比例函数图象上点的坐标特征（共2小题）
6．如图，在平面直角坐标系中，四边形OABC为矩形，点C，A分别在x轴和y轴的正半轴上，点D为AB的中点．已知实数k≠0，一次函数y＝﹣3x+k的图象经过点C、D，反比例函数y＝（x＞0）的图象经过点B，求k的值．

【分析】由y＝﹣3x+k求得C为（，0），即可得出B的横坐标，代入y＝（x＞0）求得纵坐标为3，从而求得D的坐标，代入y＝﹣3x+k即可求得k的值．
【解答】解：把y＝0代入y＝﹣3x+k，得x＝，
∴C（，0），
.∵BC⊥x轴，
∴点B横坐标为，
把x＝代入y＝，得y＝3，
∴B（，3），
∵点D为AB的中点，
∴AD＝BD．
∴D（，3），
∵点D在直线y＝﹣3x+k上，
∴3＝﹣3×+k，
∴k＝6．
【点评】本题考查了一次函数图象上点的坐标特征，反比例函数图象上点的坐标特征，矩形的性质，表示出点的坐标是解题的关键．
7．如图，A为反比例函数y＝（其中x＞0）图象上的一点，在x轴正半轴上有一点B，OB＝4．连接OA，AB，且OA＝AB＝2．
（1）求k的值；
（2）过点B作BC⊥OB，交反比例函数y＝（其中x＞0）的图象于点C，连接OC交AB于点D，求的值．

【分析】（1）过点A作AH⊥x轴，垂足为点H，AH交OC于点M，利用等腰三角形的性质可得出DH的长，利用勾股定理可得出AH的长，进而可得出点A的坐标，再利用反比例函数图象上点的坐标特征即可求出k值；
（2）由OB的长，利用反比例函数图象上点的坐标特征可得出BC的长，利用三角形中位线定理可求出MH的长，进而可得出AM的长，由AM∥BC可得出△ADM∽△BDC，利用相似三角形的性质即可求出的值．
【解答】解：（1）过点A作AH⊥x轴，垂足为点H，AH交OC于点M，如图所示．
∵OA＝AB，AH⊥OB，
∴OH＝BH＝OB＝2，
∴AH＝＝6，
∴点A的坐标为（2，6）．
∵A为反比例函数y＝图象上的一点，
∴k＝2×6＝12．
（2）∵BC⊥x轴，OB＝4，点C在反比例函数y＝上，
∴BC＝＝3．
∵AH∥BC，OH＝BH，
∴MH＝BC＝，
∴AM＝AH﹣MH＝．
∵AM∥BC，
∴△ADM∽△BDC，
∴＝＝．

【点评】本题考查了反比例函数图象上点的坐标特征、等腰三角形的性质、勾股定理以及相似三角形的判定与性质，解题的关键是：（1）利用等腰三角形的性质及勾股定理，求出点A的坐标；（2）利用相似三角形的性质求出的值．
七．全等三角形的判定与性质（共1小题）
8．问题1：如图①，在四边形ABCD中，∠B＝∠C＝90°，P是BC上一点，PA＝PD，∠APD＝90°．求证：AB+CD＝BC．
问题2：如图②，在四边形ABCD中，∠B＝∠C＝45°，P是BC上一点，PA＝PD，∠APD＝90°．求的值．

【分析】（1）由“AAS”可知△BAP≌△CPD，可得BP＝CD，AB＝PC，可得结论；
（2）过点A作AE⊥BC于E，过点D作DF⊥BC于F，由（1）可知EF＝AE+DF，由等腰直角三角形的性质可得BE＝AE，CF＝DF，AB＝AE，CD＝DF，即可求解．
【解答】证明：（1）∵∠B＝∠APD＝90°，
∴∠BAP+∠APB＝90°，∠APB+∠DPC＝90°，
∴∠BAP＝∠DPC，
又PA＝PD，∠B＝∠C＝90°，
∴△BAP≌△CPD（AAS），
∴BP＝CD，AB＝PC，
∴BC＝BP+PC＝AB+CD；
（2）如图2，过点A作AE⊥BC于E，过点D作DF⊥BC于F，

由（1）可知，EF＝AE+DF，
∵∠B＝∠C＝45°，AE⊥BC，DF⊥BC，
∴∠B＝∠BAE＝45°，∠C＝∠CDF＝45°，
∴BE＝AE，CF＝DF，AB＝AE，CD＝DF，
∴BC＝BE+EF+CF＝2（AE+DF），
∴＝＝．
【点评】本题考查了全等三角形的判定和性质，等腰直角三角形的性质，添加恰当辅助线构造全等三角形是本题的关键．
八．圆内接四边形的性质（共1小题）
9．如图，四边形ABCD内接于⊙O，∠1＝∠2，延长BC到点E，使得CE＝AB，连接ED．
（1）求证：BD＝ED；
（2）若AB＝4，BC＝6，∠ABC＝60°，求tan∠DCB的值．

【分析】（1）根据圆内接四边形的性质得到∠A＝∠DCE，证明△ABD≌△DCE，根据全等三角形的性质证明结论；
（2）过点D作DM⊥BE于M，根据等腰三角形的性质求出BM，进而求出CM，根据正切的定义求出DM，根据正切的定义计算，得到答案．
【解答】（1）证明：∵四边形ABCD内接于⊙O，
∴∠A＝∠DCE，
∵∠1＝∠2，
∴＝，
∴AD＝DC，
在△ABD和△DCE中，
，
∴△ABD≌△CED（SAS），
∴BD＝ED；
（2）解：过点D作DM⊥BE于M，
∵AB＝4，BC＝6，CE＝AB，
∴BE＝BC+EC＝10，
∵BD＝ED，DM⊥BE，
∴BM＝ME＝BE＝5，
∴CM＝BC﹣BM＝1，
∵∠ABC＝60°，∠1＝∠2，
∴∠2＝30°，
∴DM＝BM•tan∠2＝5×＝，
∴tan∠DCB＝＝．

【点评】本题考查的是圆内接四边形的性质、解直角三角形、全等三角形的判定和性质，掌握圆内接四边形的对角互补、锐角三角函数的定义是解题的关键．
九．旋转的性质（共1小题）
10．如图，△ABC中，点E在BC边上，AE＝AB，将线段AC绕A点旋转到AF的位置，使得∠CAF＝∠BAE，连接EF，EF与AC交于点G．
（1）求证：EF＝BC；
（2）若∠ABC＝65°，∠ACB＝28°，求∠FGC的度数．

【分析】（1）由旋转的性质可得AC＝AF，利用SAS证明△ABC≌△AEF，根据全等三角形的对应边相等即可得出EF＝BC；
（2）根据等腰三角形的性质以及三角形内角和定理求出∠BAE＝180°﹣65°×2＝50°，那么∠FAG＝50°．由△ABC≌△AEF，得出∠F＝∠C＝28°，再根据三角形外角的性质即可求出∠FGC＝∠FAG+∠F＝78°．
【解答】（1）证明：∵∠CAF＝∠BAE，
∴∠BAC＝∠EAF．
∵将线段AC绕A点旋转到AF的位置，
∴AC＝AF．
在△ABC与△AEF中，
，
∴△ABC≌△AEF（SAS），
∴EF＝BC；

（2）解：∵AB＝AE，∠ABC＝65°，
∴∠BAE＝180°﹣65°×2＝50°，
∴∠FAG＝∠BAE＝50°．
∵△ABC≌△AEF，
∴∠F＝∠C＝28°，
∴∠FGC＝∠FAG+∠F＝50°+28°＝78°．
【点评】本题考查了旋转的性质，全等三角形的判定与性质，等腰三角形的性质，三角形内角和定理以及三角形外角的性质，证明△ABC≌△AEF是解题的关键．
一十．相似三角形的判定与性质（共1小题）
11．如图，在矩形ABCD中，E是BC的中点，DF⊥AE，垂足为F．
（1）求证：△ABE∽△DFA；
（2）若AB＝6，BC＝4，求DF的长．

【分析】（1）由矩形性质得AD∥BC，进而由平行线的性质得∠AEB＝∠DAF，再根据两角对应相等的两个三角形相似；
（2）由E是BC的中点，求得BE，再由勾股定理求得AE，再由相似三角形的比例线段求得DF．
【解答】解：（1）∵四边形ABCD是矩形，
∴AD∥BC，∠B＝90°，
∴∠DAF＝∠AEB，
∵DF⊥AE，
∴∠AFD＝∠B＝90°，
∴△ABE∽△DFA；

（2）∵E是BC的中点，BC＝4，
∴BE＝2，
∵AB＝6，
∴AE＝，
∵四边形ABCD是矩形，
∴AD＝BC＝4，
∵△ABE∽△DFA，
∴，
∴．

【点评】本题主要考查了矩形的性质，相似三角形的性质与判定，勾股定理，关键是证明三角形相似．
一十一．用样本估计总体（共1小题）
12．某校九年级640名学生在“信息素养提升”培训前、后各参加了一次水平相同的测试，并以同一标准折算成“6分”、“7分”、“8分”、“9分”、“10分”5个成绩．为了解培训效果，用抽样调查的方式从中抽取了32名学生的2次测试成绩，并用划记法制成了如表表格：
训前
成绩（分）
6
7
8
9
10
划记
正正

正
正

人数（人）
12
4
7
5
4
培训后
成绩（分）
6
7
8
9
10
划记

一

正
正正正
人数（人）
4
1
3
9
15
（1）这32名学生2次测试成绩中，培训前测试成绩的中位数是m，培训后测试成绩的中位数是n，则m　＜　n；（填“＞”、“＜”或“＝”）
（2）这32名学生经过培训，测试成绩为“6分”的百分比比培训前减少了多少？
（3）估计该校九年级640名学生经过培训，测试成绩为“10分”的学生增加了多少人？
【分析】（1）根据中位数的定义即可得到结论；
（2）根据题意列式计算即可；
（3）根据题意列式计算即可．
【解答】解：∵培训前测试成绩的中位数m＝＝7.5，培训后测试成绩的中位数n＝＝9，
∴m＜n；
故答案为：＜；
（2）培训前：×100%，培训后：×100%，
×100%﹣×100%＝25%，
答：测试成绩为“6分”的百分比比培训前减少了25%；
（3）培训前：640×＝80，培训后：640×＝300，
300﹣80＝220，
答：测试成绩为“10分”的学生增加了220人．
【点评】本题考查了用样本估计总体，中位数，熟练掌握中位数的定义是解题的关键．
一十二．条形统计图（共2小题）
13．某学校计划在八年级开设“折扇”、“刺绣”、“剪纸”、“陶艺”四门校本课程，要求每人必须参加，并且只能选择其中一门课程，为了解学生对这四门课程的选择情况，学校从八年级全体学生中随机抽取部分学生进行问卷调查，并根据调查结果绘制成如图所示的条形统计图和扇形统计图（部分信息未给出）．

请你根据以上信息解决下列问题：
（1）参加问卷调查的学生人数为 　50　名，补全条形统计图（画图并标注相应数据）；
（2）在扇形统计图中，选择“陶艺”课程的学生占 　10　%；
（3）若该校八年级一共有1000名学生，试估计选择“刺绣”课程的学生有多少名？
【分析】（1）根据折扇的人数和所占的百分比，求出调查的学生总人数，再用总人数减去其它课程的人数，求出剪纸的人数，从而补全统计图；
（2）用选择“陶艺”课程的学生数除以总人数即可；
（3）用八年级的总人数乘以选择“刺绣”课程的学生所占的百分比即可．
【解答】解：（1）参加问卷调查的学生人数为＝50（名），
剪纸的人数有：50﹣15﹣10﹣5＝20（名），补全统计图如下：
故答案为：50；

（2）在扇形统计图中，选择“陶艺”课程的学生所占的百分比是：×100%＝10%．
故答案为：10；

（3）1000×＝200（名），
答：估计选择“刺绣”课程的学生有200名．
【点评】本题考查条形统计图、扇形统计图、用样本估计总体，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．
14．某学校计划在“阳光体育”活动课程中开设乒乓球、羽毛球、篮球、足球四个体育活动项目供学生选择．为了估计全校学生对这四个活动项目的选择情况，体育老师从全体学生中随机抽取了部分学生进行调查（规定每人必须并且只能选择其中的一个项目），并把调查结果绘制成如图所示的不完整的条形统计图和扇形统计图，请你根据图中信息解答下列问题：

（1）求参加这次调查的学生人数，并补全条形统计图；
（2）求扇形统计图中“篮球”项目所对应扇形的圆心角度数；
（3）若该校共有600名学生，试估计该校选择“足球”项目的学生有多少人？
【分析】（1）由“乒乓球”人数及其百分比可得总人数，根据各项目人数之和等于总人数求出“羽毛球”的人数，补全图形即可；
（2）用“篮球”人数占被调查人数的比例乘以360°即可；
（3）用总人数乘以样本中足球所占百分比即可得．
【解答】解：（1），
答：参加这次调查的学生人数是50人；
补全条形统计图如下：

（2），
答：扇形统计图中“篮球”项目所对应扇形的圆心角度数是72°；
（3），
答：估计该校选择“足球”项目的学生有96人．
【点评】本题考查了条形统计图和扇形统计图，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
一十三．列表法与树状图法（共2小题）
15．一只不透明的袋子中装有1个白球，3个红球，这些球除颜色外都相同．
（1）搅匀后从中任意摸出1个球，这个球是白球的概率为 　　；
（2）搅匀后从中任意摸出1个球，记录颜色后放回，搅匀，再从中任意摸出1个球，求2次摸到的球恰好是1个白球和1个红球的概率．（请用画树状图或列表等方法说明理由）
【分析】（1）直接利用概率公式求解即可求得答案；
（2）画树状图列举出所有等可能出现的情况，从中找出两个球颜色不同的结果数，进而求出概率．
【解答】解：（1）∵一只不透明的袋子中装有1个白球和3个红球，这些球除颜色外都相同，
∴搅匀后从中任意摸出1个球，则摸出白球的概率为：＝．
故答案为：；
（2）画树状图如图所示：

共有16种不同的结果数，其中两个球颜色不同的有6种，
∴2次摸到的球恰好是1个白球和1个红球的概率为＝．
【点评】考查列表法或树状图法求等可能事件发生的概率，使用此方法一定注意每一种结果出现的可能性是均等的，即为等可能事件．
16．在一个不透明的布袋中装有三个小球，小球上分别标有数字0、1、2，它们除数字外都相同．小明先从布袋中任意摸出一个小球，记下数字作为平面直角坐标系内点A的横坐标，将此球放回、搅匀，再从布袋中任意摸出一个小球，记下数字作为平面直角坐标系内点A的纵坐标．请用树状图或表格列出点A所有可能的坐标，并求出点A在坐标轴上的概率．
【分析】用树状图或列表法表示所有可能出现的结果，进而求出相应的概率．
【解答】解：用列表格法表示点A所有可能的情况如下：

共有9种等可能出现的结果，其中点A在坐标轴上有5种，
∴P（点A在坐标轴上）＝．
【点评】考查树状图或列表法求随机事件发生的概率，列举出所有可能出现的结果是解决问题的关键．
一十四．游戏公平性（共1小题）
17．4张相同的卡片上分别写有数字0、1、﹣2、3，将卡片的背面朝上，洗匀后从中任意抽取1张，将卡片上的数字记录下来；再从余下的3张卡片中任意抽取1张，同样将卡片上的数字记录下来．
（1）第一次抽取的卡片上数字是负数的概率为 　　；
（2）小敏设计了如下游戏规则：当第一次记录下来的数字减去第二次记录下来的数字所得结果为非负数时，甲获胜；否则，乙获胜．小敏设计的游戏规则公平吗？为什么？（请用树状图或列表等方法说明理由）
【分析】（1）利用概率公式求解即可；
（2）利用列表法列举出所有可能，进而利用概率公式进而得出甲、乙获胜的概率即可得出答案．
【解答】解：（1）第一次抽取的卡片上数字是负数的概率为，
故答案为：．
（2）列表如下：

0
1
﹣2
3
0

1
﹣2
3
1
﹣1

﹣3
2
﹣2
2
3

5
3
﹣3
﹣2
﹣5

由表可知，共有12种等可能结果，其中结果为非负数的有6种结果，结果为负数的有6种结果，
所以甲获胜的概率＝乙获胜的概率＝＝，
∴此游戏公平．
【点评】本题考查的是游戏公平性的判断．判断游戏公平性就要计算每个参与者取胜的概率，概率相等就公平，否则就不公平．用到的知识点为：概率＝所求情况数与总情况数之比．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2023/4/13 21:40:43；用户：19105418363；邮箱：19105418363；学号：36567650

菁优网APP 菁优网公众号 菁优网小程序