






所属成套资源:(通用版)中考数学一轮复习练习课件专题 (含答案)
(通用版)中考数学一轮复习练习课件专题3.6 二次函数的综合(一题18变) (含答案)
展开这是一份(通用版)中考数学一轮复习练习课件专题3.6 二次函数的综合(一题18变) (含答案),共31页。PPT课件主要包含了0-3,求函数的关系式,x1-x2,y1-y2,在抛物线上求点的坐标,抛物线与角度的关系,抛物线与特殊三角形,抛物线与相似三角形,抛物线与特殊四边形,∴yNyC等内容,欢迎下载使用。
【引例】已知:如图,抛物线L:y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,OA=OC=3,顶点为D.求此函数的关系式;
解:∵OA=OC=3, ∴A(-3,0),C(0,-3)代入y=x2+bx+c可得:
∴此函数的解析式为:y=x2+2x-3
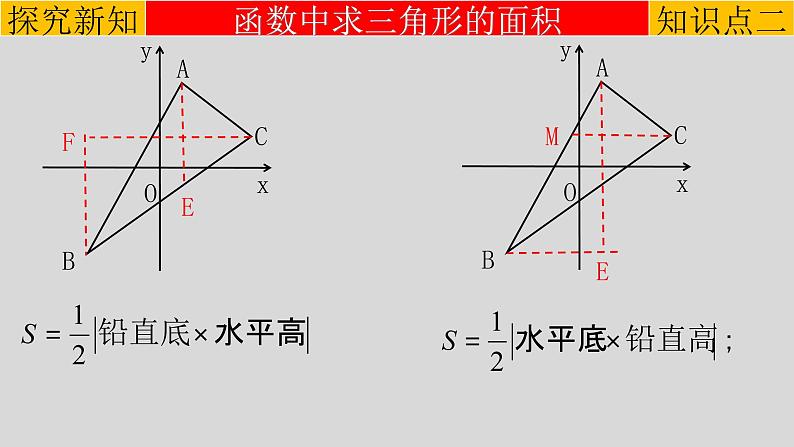
【情况1】线段与坐标轴平行①当线段与x轴平行,AB=_______.
【情况2】线段与坐标轴不平行
【情况3】线段AB的中点C的坐标
②当线段与y轴平行,AB=_______.
在抛物线上求最大(小)值
1.在抛物线y=x2+2x-3上是否存在一点N,使S△ABN=S△ABC,若存在,求出点N的坐标;若不存在,说明理由.
解:存在.∵△ABN与△ABC同底
∴当△ABN与△ABC等高时,S△ABN=S△ABC
即:x2+2x-3=±3
2.在抛物线y=x2+2x-3上是否存在一点Q,使S△AOQ=S△COQ?若存在,求出点Q的坐标;若不存在,说明理由.
存在,∵OA=OC=3,S△AOQ=S△COQ
∴点Q的横坐标相等或互为相反数,作直线y=±x,与抛物线y=x2+2x-3的交点便是符合要求的Q点,
3.在线段AC下方的抛物线y=x2+2x-3上有一点N,过点N作直线n∥y轴,交AC与点M,当点N坐标为多少时,线段MN的长度最大值是多少?
设点N的坐标为(t,t2+2t-3)
则点M的坐标为(t,-t-3)
∴MN=(-t-3)-(t2+2t-3)=-(t+3/2)2+9/4.
∴当t=-3/2时,MNmax=9/4,此时t2+2t-3=-15/4.
∴点N的坐标为(-3/2,-15/4)时, 线段MN的长度最大值为9/4.
4.在抛物线y=x2+2x-3对称轴上找一点P,使△BCP的周长最小,求出P点坐标及△BPC的周长.
利用将军饮马模型可求得:
点P的坐标为(-1,-2).
5.在AC下方的抛物线y=x2+2x-3上,是否存在一点N使△CAN面积最大?最大面积是多少?
方法一:存在,过点N作NE⊥x轴于点E,交AC于点M.
设点N的坐标为(t,t2+2t-3)则点M的坐标为(t,-t-3)
S△CAN=S△CAN+S△CAN=1/2MN·AE+1/2MN·OE=1/2MN·AO =1/2(-t2-3t)·3=-3/2(t+3/2)2+27/8
当t=-3/2时,N(-3/2,-15/4),△CAN面积最大值为27/8.
方法二:连接ON,设点N的坐标为(t,t2+2t-3).
S△CAN=S△AON+S△CON-S△BOC=1/2AO·|yN|+1/2CO·|xN|-1/2×1×2
=1/2×3(t2+2t-3)+1/2×3t-3=-3/2(t+3/2)2+27/8
6.直线y=x-1与抛物线y=x2+2x-3交于点B,M,在BM下方的抛物线是否存在一点N使△BMN面积最大?最大面积是多少?
方法一:存在,过点N作NE⊥x轴于点E,交BM于点F.
方法二:过M作MH⊥AB于点H,连接HN,
=1/2(-t2-t+2)·3=-3/2(t+1/2)2+27/8
设点N的坐标为(t,t2+2t-3)则点F的坐标为(t,t-1)
∴NF=-t2-t+2,M(-2,-3).
当t=-1/2时,N(-1/2,-15/4),△BMN面积最大值为27/8.
S△BMN=1/2·NF·(xB-xM)
设N(t,t2+2t-3).
S△BMN=S△HMN+S△HBN-S△HMB=0.5×3(t+2)+0.5×3·|t2+2t-3|-0.5×3×3
=-3/2(t+1/2)2+27/8
7.在AC下方的抛物线y=x2+2x-3上,是否存在一点N,使四边形ABCN面积最大,且最大面积是多少?
方法一:S四边形ABCN=S△ABE+S梯形OCNE+S△OBC.
方法二:S四边形ABCN=S△OAN+S△OCN+S△OBC.
8.如图,抛物线y=x2+2x-3交x轴于A,B两点(点A在的B的左边),交y的负半轴于点C,若抛物线上有一点D,∠BCD=45º,求点D的坐标.
解:过B作BK⊥BC交CD于点K,过K作KH⊥x轴于点H,
∴AH=CO=3,KH=OA=1.
9.如图,抛物线y=x2+4x+3与x轴交于A、B两点,与y轴交于点C,点P在抛物线上,∠PCA=∠BCA,求点P的坐标.
解:过A作AE⊥AB,使AE=AB=2.
∴直线CE为y=1/3x+3
得P(-11/3,16/9)
9.判断△ACD的形状,并说明理由;
如图,△ACD是直角三角形,理由如下:
∵y=x2+2x-3=(x+1)2-4.∴D(-1,-4),
∵AC2=OA2+OC2=32+32=18,CD2=12+12=2,AD2=22+42=20.
∴AC2+CD2=AD2
∴△ACD是直角三角形.
10.在y轴上是否存在一点E,使△ADE为直角三角形,若存在,求出E的坐标,若不存在,说明理由.
存在.设点E1(0,t),
则AD2+AE12=DE12,
则AE2=t2+9,DE2=(t+4)2+1=t2+8t+17,AD2=(-1+3)2+42=20
②当∠ADE=90º时,
即:20+t2+8t+17=t2+9
∴E2(0,-3.5)
则AD2+DE22=AE22,
③当∠AED=90º时,
则AE2+DE2=AD2,∴t2+9+(t+4)2+1=20
解得:t1=-3,t2=-1,
∴E3(0,-3),E4(0,-1)
综上所述,点E的坐标分别为(0,1.5),(0,-3.5),(0,-3),(0,-1)
①当∠DAE=90º时,
即:20+t2+9=t2+8t+17
即:t2+9+t2+8t+17=20
11.在y轴上是否存在一点F,使△ADF为等腰三角形,若存在,求出点F的坐标;若不存在,说明理由
则t2+9=t2+8t+17.
则t2+8t+17=20.
则AF2=t2+9,DF2=(t+4)2+1=t2+8t+17,AD2=(-1+3)2+42=20
12.求A、B、C三点共圆的圆心坐标及所在圆的半径大小.
△ABC的外心在AB与AC的垂直平分线的交点,
即抛物线的对称轴与直线y=x的交点(-1,-1)
13.求A、C、D三点共圆的圆心坐标及所在圆的半径大小.
设△ABD的外心坐表为I(m,n)
IA2=(m+3)2+n2;
ID2=(m+1)2+(n+4)2;
IC2=m2+(n+3)2;
∵IA2=ID2=IC2.
∴外心为(-2,-2),半径为
14.在线段AC上是否存在点M,使△AOM与△ABC相似?若存在,求出点M的坐标;若不存在,说明理由.
∴AG2+MG2=AM2
①当∴△AOM∽△ABC,
存在∵OA=OC=3,∴△AOC为等腰直角三角形,∴∠BAC=45º,AB=4,
②当△AOM∽△ACB,
∵MG⊥AB,∴AG2+MG2=AM2,
∴OG=AO-AG=3-2=1,
15.点P是抛物线上一个动点,作PH⊥x轴于H,是否存在点P,使得△PAH与△OBC相似?若存在,求出点P的坐标;若不存在,说明理由.
存在,如图,∵∠PHA=∠BOC=90º,要使△PAH与△OBC相似,
设P(t,t2+2t-3),
解得:t3=4,t4=-2.
当t=4时,t2+2t-3=21,
当t=-2时,t2+2t-3=-3,
∴P3(4,21),P4(-2,-3).
综上所述:抛物线上存在4个点P,使得△PAH与△OBC相似,相应坐标分别为
16.E在对称轴上,F在抛物线上,若A,B,E,F为顶点形成平行四边形,求出E,F点的坐标.
①以AB为边,则EF∥AB,且EF=AB.
设F(m,m2+2m-3),则E(-1,m2+2m-3).
解得:m1=3,m2=-5
当m=3时,m2+2m-3=12;当m=-5时,m2+2m-3=12
②以AB为对角线,则AB与EF互相平分,
∴点F与D重合,E与D关于AB对称.
综上所述:F(3,12),E(-1,12)或F(-5,12),E(-1,12) 或F(-1,-4),E(-1,4).
17.E在对称轴上,F在抛物线上,若A,O,E,F为顶点形成平行四边形,求出E,F点的坐标.
①以AO为边,则EF∥AO,且EF=AO.
解得:m1=2,m2=-4
当m=2时,m2+2m-3=5;当m=-4时,m2+2m-3=5
②以A0为对角线,则A0与EF互相平分,
∵AO的中点M(-1.5,0)
综上所述:F(2,5),E(-1,5)或F(-4,5),E(-1,5)或F(-2,-3),E(-1,3).
把F(-2,-n)代入y=x2+2x-3得n=-3.
∴E(-1,3),F(-2,-3)
相关课件
这是一份(经典版)中考数学一轮考点复习精品课件专题3.6 二次函数的综合(一题18变) (含解析),共31页。PPT课件主要包含了0-3,求函数的关系式,x1-x2,y1-y2,在抛物线上求点的坐标,抛物线与角度的关系,抛物线与特殊三角形,抛物线与相似三角形,抛物线与特殊四边形,∴yNyC等内容,欢迎下载使用。
这是一份(通用版)中考数学一轮复习练习课件专题8.1 统计 (含答案),共26页。PPT课件主要包含了数据的分析,综合应用,拓展训练,考点聚焦,考察对象较多,调查具有破坏性,考察对象较少,百分比,变化趋势,温馨提示等内容,欢迎下载使用。
这是一份(通用版)中考数学一轮复习练习课件专题3.5 二次函数的最值问题 (含答案),共25页。PPT课件主要包含了拓展训练,h≥3,∵y轴为对称轴,∴a0,∴b2a2+4a,∴对称轴为x-2,yax2+bx+c,D定点,8-x,-25或8等内容,欢迎下载使用。












