【江苏专用】2023年中考数学易错题汇编——03 函数（原卷版+解析版）

这是一份【江苏专用】2023年中考数学易错题汇编——03 函数（原卷版+解析版），文件包含03函数解析版docx、03函数原卷版docx等2份试卷配套教学资源，其中试卷共73页， 欢迎下载使用。
一次函数的图像与性质
一次函数的应用
反比例函数
二次函数的图像性质与性质
二次函数的应用
易错分析 01
各个待定系数表示的意义。充分掌握一次函数，反比例函数以及二次函数的概念。
对于较复杂问题容易忽略数形结合思想。
（2022九下·沭阳模拟）已知一次函数y＝kx＋b，且当－3≤x≤1时，1≤y≤9，则k＋b的值为
【答案】9
【规范解答】本题答案不全面，此题分两种情况考虑：①当x=-3时，y=1；当x=1时，y=9，代入y=kx+b中求出k、b的值，进而可得k+b的值；②当x=-3时，y=9，当x=1时，y=1，同理可得k+b的值.
【规范解答】解：①当x=-3时，y=1；当x=1时，y=9；
则1=-3k+b9=k+b，
解得k=2b=7，
；
②当x=-3时，y=9，当x=1时，y=1；
则9=-3k+b1=k+b，
解得，
；
故答案为：9或1.
【变式训练01】（2022·宿迁）甲、乙两位同学各给出某函数的一个特征，甲：“函数值y随自变量x增大而减小”；乙：“函数图象经过点(0，2)”，请你写出一个同时满足这两个特征的函数，其表达式是 .
【答案】y=-2x+2（答案不唯一）
【规范解答】解：根据题意，甲：“函数值y随自变量x增大而减小”；
可设函数为：
又满足乙：“函数图象经过点(0，2)”，
则函数关系式为y=-2x+2，
故答案为：y=-2x+2（答案不唯一）
【思路点拨】根据一次函数的性质结合题意可设y=-2x+b，将（0，2）代入求出b的值，进而可得对应的函数关系式.
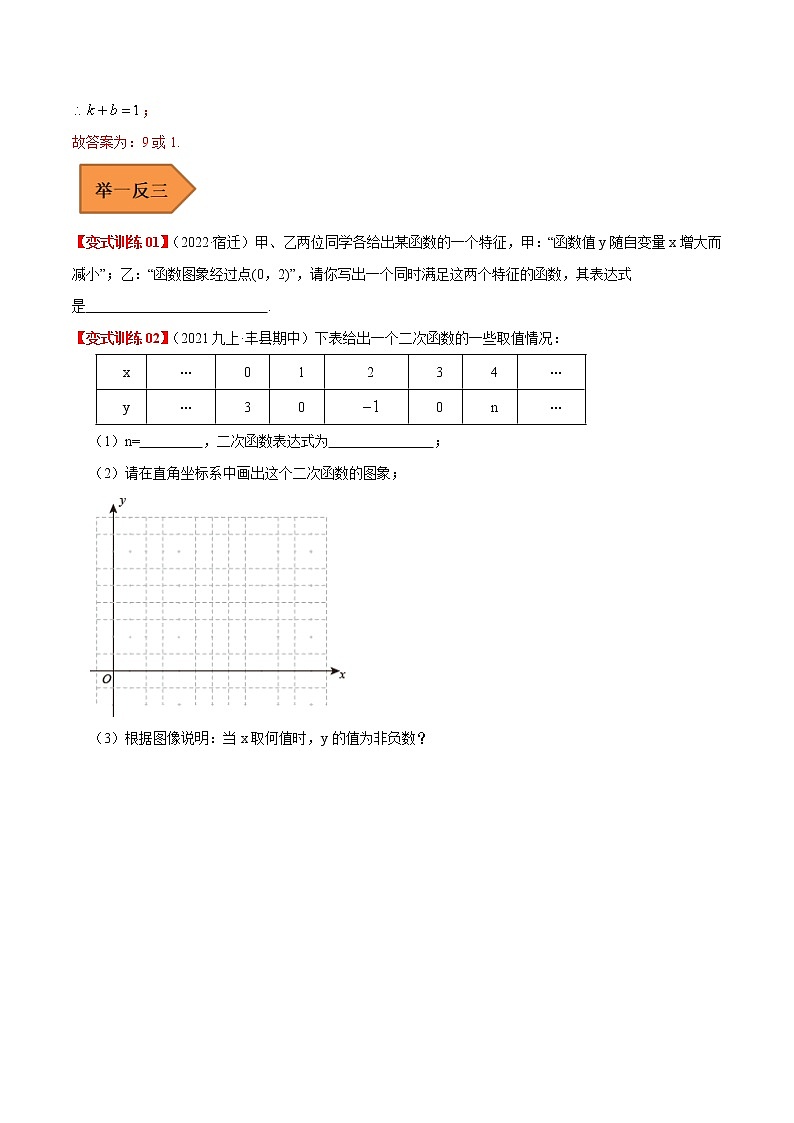
【变式训练02】（2021九上·丰县期中）下表给出一个二次函数的一些取值情况：
（1）n= ，二次函数表达式为 ；
（2）请在直角坐标系中画出这个二次函数的图象；
（3）根据图像说明：当x取何值时，y的值为非负数？
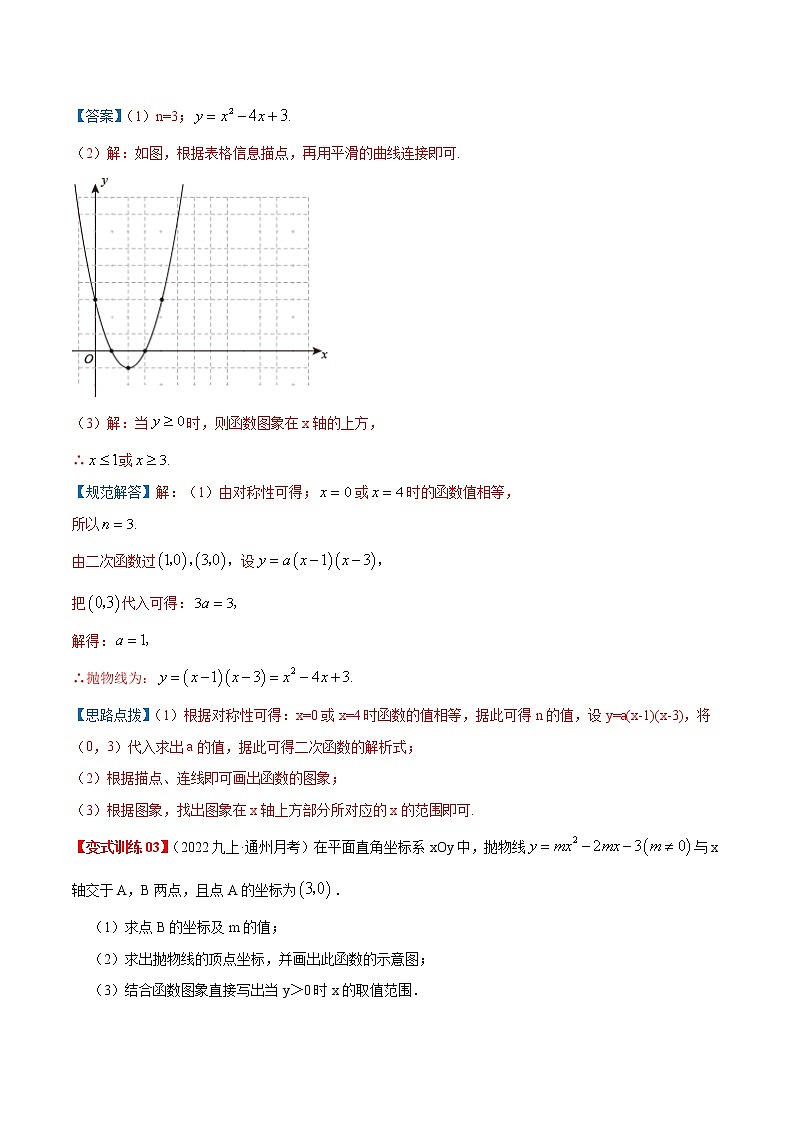
【答案】（1）n=3；
（2）解：如图，根据表格信息描点，再用平滑的曲线连接即可.
（3）解：当时，则函数图象在x轴的上方，
∴或
【规范解答】解：（1）由对称性可得；或时的函数值相等，
所以
由二次函数过 设
把代入可得：
解得：
∴抛物线为：
【思路点拨】（1）根据对称性可得：x=0或x=4时函数的值相等，据此可得n的值，设y=a(x-1)(x-3)，将（0，3）代入求出a的值，据此可得二次函数的解析式；
（2）根据描点、连线即可画出函数的图象；
（3）根据图象，找出图象在x轴上方部分所对应的x的范围即可.
【变式训练03】（2022九上·通州月考）在平面直角坐标系xOy中，抛物线与x轴交于A，B两点，且点A的坐标为．
（1）求点B的坐标及m的值；
（2）求出抛物线的顶点坐标，并画出此函数的示意图；
（3）结合函数图象直接写出当y＞0时x的取值范围．
【答案】（1）解：把代入，
得9m-6m-3=0，解得m=1，
抛物线解析式为，
当y=0时，，解得，，
所以B点坐标为；
（2）解：，则抛物线的顶点坐标为，
列表如下：
描点、连线，
（3）解：由函数图象可知，当y＞0时，x＜-1或x＞3，即x的取值范围是x＜-1或x＞3．
【思路点拨】（1）将点A的坐标代入函数解析式，可得到关于m的方程，解方程求出m的值，可得到函数解析式；由y=0，可得到关于x的方程，解方程求出m的值，可得到点B的坐标.
（2）利用配方法将函数解析式转化为顶点式，可得到抛物线的顶点坐标；再列表，描点，连线，画出函数图象.
（3）观察函数图象（x轴上方的图象），可得到当y＞0时x的取值范围.
易错分析 02
各种函数解析式的求法以及函数与几何图形的关系应用。注意解析式中字母表示的几何意义，特别是二次函数的解析式，其表示的方式多样化，容易记忆混淆。涉及的公式比较多，一定要理解推导记忆
6．（2022九上·通州月考）已知二次函数的部分图象如图所示，则关于x的一元二次方程的解为 ．
【答案】
【解析】本题答案不全面，利用二次函数的解析式可得到抛物线的对称轴为直线x=1，观察图象可知抛物线与x轴的一个交点坐标为（4，0），利用二次函数的对称性，可得到抛物线与x轴的另一个交点坐标；然后就二次函数y=-x2+2x+m与x轴的交点的横坐标就是一元二次方程-x2+2x+m=0的两个根，即可求解.
【规范解答】解：根据图象可知，二次函数的部分图象经过点（4，0），
对称轴为，
由抛物线的对称性可知：二次函数与x轴的另一个交点坐标为：
抛物线与x轴交点坐标的横坐标即为一元二次方程的根，即：；
故答案为：．
【变式训练01】（2022九上·通州月考）抛物线的对称轴是（ ）
A．直线x＝﹣1B．直线x＝1C．直线x＝﹣2D．直线x＝2
【答案】B
【规范解答】解：∵，
∴该抛物线的对称轴是直线x＝1，
故答案为：B．
【思路点拨】利用抛物线y=a（x-h）2+k的对称轴为直线x=h，由此可得到已知抛物线的对称轴.
【变式训练02】（2022九上·通州月考）设A（﹣2，y1），B（1，y2），C（2，y3）是抛物线y＝x2﹣2x+c上的三点，y1，y2，y3的大小关系为（ ）
A．y1＞y2＞y3B．y1＞y3＞y2C．y3＞y2＞y1D．y3＞y1＞y2
【答案】B
【规范解答】解：∵y＝x2﹣2x+c，
∴抛物线开口向上，对称轴为直线x＝1，
∵1﹣（﹣2）＞2﹣1＞1﹣1，
∴y1＞y3＞y2．
故答案为：B．
【思路点拨】利用二次函数解析式可知抛物线开口向上，对称轴为直线x＝1，再利用二次函数的增减性，可得到y1，y2，y3的大小关系.
【变式训练03】（2022九上·兴化开学考）已知反比例函数y，下列说法不正确的是（ ）
A．图像经过点（2，﹣4）B．图像分别在二、四象限
C．当y≤1时，x≤﹣8D．在每个象限内，y随x增大而增大
【答案】C
【规范解答】解：A、当x=2时，y=-4，即 反比例函数y的图像经过点（2，-4），A说法正确；
B、因为反比例函数y中的k=-8，所以图像分别在二、四象限，B说法正确；
C、y≤1时，x≥-8，C说法不正确；
D、因为反比例函数y中的k=-8，所以在每个象限内，y随x增大而增大，D说法正确；
故答案为：C.
【思路点拨】反比例函数的性质：对于反比例函数，当k>0，反比例函数图象在一、三象限，每个象限内，y随x的增大而减小；当k0，代入化简可得b=-2k，根据不等式表示出x，进而可得x的范围.
【规范解答】解：∵根据图象可知y＝kx＋b与x轴交于点，且，
∴，
解得，
，
∴，
即，
解得x＞3.
故答案为：x＞3.
【思路点拨】根据图象可知y＝kx+b与x轴交于点（2，0）且k>0，代入化简可得b=-2k，根据不等式表示出x，进而可得x的范围.
【变式训练01】（2022·扬州）如图，函数的图象经过点，则关于的不等式的解集为 .
【答案】x＜-1
【规范解答】解：由一次函数图象得，当y>3时，x＜-1，
则y=kx+b>3的解集是x＜-1.
故答案为：x＜-1.
【思路点拨】 求不等式的解集， 根据图象可得，就是求点P左边图象上点的自变量的取值范围，据此即可得出答案.
【变式训练02】（2021·阜宁模拟）已知一次函数 的图象如图所示，则关于 的不等式 的解集为 .
【答案】x＞2
【规范解答】由题意得，一次函数y=kx+b的图象经过（-4，0），k＜0，
∴-4k+b=0，
∴b=4k，
∴不等式可化为：2kx-4k＜0，
解得，x＞2，
故答案为：x＞2.
【思路点拨】根据一次函数图象上点的坐标特征得到b=4k，k＜0，解不等式得到答案.
【变式训练03】（2021·滨海模拟）如图，两条直线l1和l2的关系式分别为y1=k1x+b1，y2=k2x+b2，两直线的交点坐标为（2，1），当y1＞y2时，x的取值范围为 .
【答案】x＜2
【规范解答】解：∵直线l1：y1=k1x+b1与直线l2：y2=k2x+b2的交点坐标是（2，1），
∴当x=2时，y1=y2=1；
而当y1＞y2时，x＜2.
故答案为：x＜2.
【思路点拨】由图象可知，求函数值 y1＞y2时 ，就是求y1的图象在y2的图象的上方部分相应的自变量的取值范围.
易错分析 04
利用函数模型解实际问题。注意区别方程、函数、不等式模型解决不等领域的问题。这类问题容易出现多个解，对审题能力，计算及概念掌握要求比较高。需要着重掌握零散的知识点
（2022·沭阳模拟）二次函数的部分图象如图所示，对称轴为直线，当时，x的取值范围是 .
【答案】
【思路点拨】答案不全面，没有考虑到图像的完整性。由图象可知：抛物线的对称轴为x=-1，与x轴的一个交点坐标为（3，0） ，则其与x轴的另一个交点坐标为（-5，0） ，然后根据图象，找出二次函数图象在x轴上方部分所对应的x的范围即可.
【规范解答】解：由图象可知，抛物线的对称轴为，
∵与轴的一个交点坐标为 ，
则其与x轴的另一个交点坐标为 ，
结合图象得：当 时， .
故答案为：.
【变式训练01】（2022·泰州）如图，二次函数的图象与y轴相交于点A，与反比例函数的图象相交于点B(3，1).
（1）求这两个函数的表达式；
（2）当随x的增大而增大且时，直接写出x的取值范围；
（3）平行于x轴的直线l与函数的图象相交于点C、D（点C在点D的左边），与函数的图象相交于点E.若△ACE与△BDE的面积相等，求点E的坐标.
【答案】（1）解：二次函数的图象与y轴相交于点A，与反比例函数的图象相交于点，
，，
解得，，
二次函数的解析式为，反比例函数的解析式为；
（2）
（3）解：由题意作图如下：
当时，，
，
，
的边上的高与的边上的高相等，
与的面积相等，
，
即E点是二次函数的对称轴与反比例函数的交点，
当时，，
.
【规范解答】解：（2）二次函数的解析式为，
对称轴为直线，
由图象知，当随x的增大而增大且时，；
【思路点拨】（1）将B（3，1）分别代入y1=x2+mx+1、y2=中进行计算可得m、k的值，据此可得二次函数以及反比例函数的解析式；
（2）根据二次函数的解析式可得对称轴，然后根据图象，找出二次函数图象在对称轴右侧、且在反比例函数图象下方部分所对应的x的范围即可；
（3）画出示意图，易得A（0，1），根据△ACE与△BDE的面积相等可得CE=DE，即E点是二次函数的对称轴与反比例函数的交点，令反比例函数解析式中的x=，求出y的值，据此可得点E的坐标.
【变式训练02】（2022·泗洪模拟）如图，二次函数y1＝﹣x2+bx+c的图象与x轴、y轴分别交于点A（﹣1，0）和点B（0，2），图象的对称轴交x轴于点C，一次函数y2＝mx+n的图象经过点B、C.
（1）求二次函数的解析式y1和一次函数的解析式y2；
（2）点P在x轴下方的二次函数图象上，且S△ACP＝33，求点P的坐标；
（3）结合图象，求当x取什么范围的值时，有y1≤y2.
【答案】（1）解：将点A（﹣1，0）和点B（0，2）代入y1＝﹣x2+bx+c，
得：，
解得：，
∴二次函数的解析式为y1＝﹣x2+x+2.
∵二次函数的对称轴为直线x＝﹣＝2，
∴C（2，0），
∵一次函数y2＝mx+n的图象经过点B、C，
∴，
解得，
∴一次函数的解析式为y2＝﹣x+2.
（2）解：设P到x的距离为h，
∵A（﹣1，0），C（2，0），
∴AC＝3，
∵S△ACP＝33，
∴AC•h＝33，
∴h＝22，
∴P的纵坐标为﹣22，
把y＝﹣22代入y1＝﹣x2+x+2，
得﹣22＝﹣x2+x+2，
解得x＝10或x＝﹣6，
∴P的坐标为（10，﹣22）和（﹣6，﹣22）；
（3）解：
得或，
∴抛物线与直线的另一个交点为（，﹣），
由图象可知，当x≤0或x≥时，有y1≤y2.
【思路点拨】（1）将点A（-1，0）和点B（0，2）代入y1＝-x2+bx+c中求出b、c的值，进而可得y1的解析式，根据解析式可得对称轴，进而得到点C的坐标，将点B、C的坐标代入y2=mx+n中求出m、n，据此可得y2的解析式；
（2）设P到x的距离为h，根据点A、C的坐标可得AC＝3，结合三角形的面积公式可求出h，进而得到点P的纵坐标，将P点的纵坐标代入y1解析式中求出x，进而可得点P的坐标；
（3）联立y1、y2解析式求出x、y，得到抛物线与直线的交点坐标，然后根据图象，找出二次函数图象在一次函数图象下方部分所对应的x的范围即可.
易错分析 05
反比例函数K值得特殊意义及应用。对相关公式加深理解记忆，这类问题在考察作辅助线以及反比例函数与几何图形的综合运用上有一定要求
（2022九下·沭阳模拟）如图，在平面直角坐标系中，函数 y=kx 与 y=的图象交于 A、B 两点，过 A 作 y 轴的垂线，交函数的图象于点 C，连接 BC，则△ABC 的面积为（ ）
A．2B．4C．6D．8
【答案】B
【思路点拨】答案有误。忽略了辅助线的解题技巧。连接OC，设AC⊥y轴交y轴为点D，由反比例函数的对称性得OA=OB，根据等底同高三角形面积相等得S△AOC=S△COB，根据反比例函数k的几何意义可得S△AOD=1，S△COD=2，则S△AOC=3，据此计算.
【规范解答】解：连接OC，设AC⊥y轴交y轴为点D，
如图，
∵反比例函数y=-为对称图形，
∴O为AB的中点，
∴S△AOC=S△COB，
∵由题意得A点在y=-上，B点在y=上，
∴S△AOD==1，S△COD=2；
S△AOC= S△AOD+ S△COD=3，
∴S△ABC= S△AOC+S△COB=6.
故答案为：C.
【变式训练01】（2022·锡山模拟）如图，在平面直角坐标系中，C，A分别为x轴、y轴正半轴上的点，以OA，OC为边，在第一象限内作矩形OABC，且S矩形OABC＝2 ，将矩形OABC翻折，使点B与原点O重合，折痕为MN，点C的对应点C'落在第四象限，过M点的反比例函数y＝ （k≠0）的图象恰好过MN的中点，则k的值为 ，点C'的坐标为 .
【答案】；
【规范解答】解：如图所示，连接OB交MN于Q，
由折叠的性质可得MO=MB，OQ=OB，
∵四边形OABC是矩形，
∴ ，
∴∠MOQ=∠NOQ，∠BMQ=∠ONQ，
又∵BQ=OQ，
∴△BMQ≌△ONQ（AAS），
∴QM=QN，即点Q为OB的中点，
过点Q作QH⊥x轴于H，
∴ ，
∴△OHQ∽△OCB，
∴ ，
∵四边形OABC是矩形，
∴ ，
∵Q在反比例函数图象上，
∴ ；
过点 作 轴于G，
∵点M在反比例函数图象上，
∴ ，
又∵ ，
∴ ，
设AM=a，则BM=OM=3a，
∴ ，
∴ ，
解得 （负值已经舍去），
∴AB=OC=2， ，
∵QM=QG，OQ=BQ，
∴四边形OMBN是平行四边形，
∴ ，
∴ ，
∴ ，
∵ ，
∴ ，
∴ ，
∴点C的坐标为
故答案为： ， .
【思路点拨】连接OB交MN于Q，由折叠得MO=MB，OQ=OB，根据矩形以及平行线的性质得∠MOQ=∠NOQ，∠BMQ=∠ONQ，证△BMQ≌△ONQ，得QM=QN，过点Q作QH⊥x轴于H，易证△OHQ∽△OCB，根据矩形的性质可得S△OHQ=S矩形OABC=，根据反比例函数k的几何意义可得k=2S△OHQ=，过点C′作C′G⊥x轴于G，易得AM=AB，设AM=a，则BM=OM=3a，由勾股定理可得OA，然后结合三角形的面积公式可得a的值，易得四边形OMBN是平行四边形，则ON=BM，CN=C′N，利用勾股定理求出OC′，根据△OC′N的面积公式可得C′G，然后利用勾股定理求出OG，据此可得点C的坐标.
【变式训练02】（2021·江都模拟）如图，平行四边形ABCO的边AB的中点F在y轴上，对角线AC与y轴交于点E，若反比例函数 （x＞0）的图象恰好经过AF的中点D，且△AEO的面积为6，则k的值为 .
【答案】9
【规范解答】解：如图，连接OD，
∵四边形ABCO是平行四边形，
∴AB∥OC，AB＝OC，
∴△AEF∽△CEO，
∴ ＝ ，
∵F是AB的中点，
∴AB＝2AF，
∴OC＝2AF，
∴ ＝ ＝ ，
∴ ＝ ＝ ，
∵△AEO的面积为6，
∴S△AEF＝ S△AEO＝ ×6＝3，
∴S△AOF＝S△AEO＋S△AEF＝6＋3＝9，
∵点D是AF的中点，
∴S△DOF＝ S△AOF＝ ，
∴ |k|＝ ，且k＞0，
∴k＝9.
故答案为：9.
【思路点拨】连接OD，由平行四边形的性质可得AB∥OC，AB＝OC，证明△AEF∽△CEO，由中点的概念可得AB＝2AF，则OC＝2AF，根据相似三角形的性质可得＝＝，由△AEO的面积为6可得S△AEF＝3，进而求出S△AOF，S△DOF，然后结合反比例函数k的几何意义进行求解.
【变式训练03】（2021·大丰模拟）如图，点 在反比例函数 （ ）的图象上，点 在反比例函数 （ ）的图象上，且 轴， ，垂足为点 ，交 轴于点 .则 的面积为（ ）
A．3B．4C．5D．6
【答案】B
【规范解答】解：过D点作y轴垂线，垂足为D，BC与x轴交于点E，
∵ 轴，点 在反比例函数 上，
∴S四边形BDOE的面积为6，
∵ ，点 在反比例函数 上，
∴S四边形AOEC的面积为2，
∴S四边形ACBD的面积为8，
∴ S四边形ACBD=4.
故答案为：B.
【思路点拨】过D点作y轴垂线，垂足为D，BC与x轴交于点E，根据反比例函数k的几何意义可得S四边形BDOE=6，S四边形AOEC=2，据此求出四边形ACBD的面积，进而可得△ABC的面积.
易错分析 06
与坐标轴交点坐标一定要会求。面积最大值的求解方法，距离之和的最小值的求解方法，距离之差最大值的求解方法。此类问题需要掌握一定的解题技巧，特别是辅助线的作法上，掌握必要的辅助线作法模型很重要，对解题速度，正确率都有很大的帮助。
（2022·南通模拟）若抛物线 的图像与 轴有交点，那么 的取值范围是 ．
【答案】m＜1
【思路点拨】答案有误，没有考虑到多种情况。令y=0，根据抛物线的图象与x轴有交点可得△≥0，代入求解可得m的范围.
【规范解答】解： 抛物线 的图像与 轴有交点，
令 ，有 ，即该方程有实数根，
，
．
故答案是：m≤1．
【变式训练01】（2022九上·盐城期末）二次函数的图象如图所示，则三个代数式①abc，②，③中，值为正数的有 .（填序号）
【答案】①②③
【规范解答】解：∵抛物线的对称轴在x轴的正半轴，且抛物线与x轴有两个不同交点，与y轴交于负半轴，
∴ab＜0，c＜0，＞0，
∴abc＞0，
如图，直线x=-1，与抛物线的交点在x轴上方，
∴＞0，
故答案为：①②③.
【思路点拨】抛物线的对称轴在x轴的正半轴（左同右异）可得ab＜0，抛物线与x轴有两个不同交点可得b2-4ac＞0，与y轴交于负半轴可得c＜0，据此可判断①和②的正负；由图可知直线x=-1，与抛物线的交点在x轴上方，即y=a-b+c＞0，据此判断③的正负.
【变式训练02】（2021九上·浦口月考）已知二次函数y＝（x－m）2－1（m为常数）.
（1）求证：不论m为何值，该函数图象与x轴总有两个公共点；
（2）请根据m的不同取值，探索该函数图象过哪些象限?（直接写出答案）
（3）当1≤x≤3时，y的最小值为3，求m的值.
【答案】（1）解：y=（x－m）2－1
y=x2－2mx＋m2－1，令y=0，x2－2mx＋m2-1=0，
∵a=1，b=-2m，c=m2-1，
∴b2－4ac＝4m2－4（m2－1）=4＞0，此方程有两个不相等的实数根，
∴该函数图象与x轴总有两个公共点；
（2）解：∵a>0，
∴图象必经过一、二象限，
令y=0，即x2－2mx＋m2-1=0，
解得x1=m-1，x2=m+1，
∴当m+1≤0，即m≤﹣1时，图象过一、二、三象限；
当-1＜m＜1时，图象过一、二、三、四象限；
当m-1>0，m≥1时，图象过一、二、四象限.
（3）解：∵a=1＞0，图象开口向上，又∵对称轴为直线x=m，
∴当m≤1时，y随x的增大而增大，当x=1时y有最小值3，
即3=（1－m）2－1，解得m1=﹣1，m2=3＞1（舍去）；
当1＜m＜3时，当x=m时，y有最小值﹣1，y的最小值为3不可能；
当m＞3时，y随x增大而减小，当x=3时y有最小值3，
即3=（3－m）2－1，解得m1=1＜3（舍去），m2=5.
答：当1≤x≤3时，y的最小值为3，m的值为-1或5.
【思路点拨】（1）二次函数y＝（x－m）2－1的图象与x轴总有两个公共点，即关于x的一元二次方程 x2－2mx＋m2-1=0 有两个不相等的实数根，故证明判别式△>0即可；
（2）由a>0，图象必经过一 、二象限，再根据函数图象与x轴的交点情况，分别进行分析判断即可；
（3）分三种情况讨论，即m≤l，1