2023年中考数学精选真题实战测试51 圆的基本概念 A

2023年中考数学精选真题实战测试51 圆的基本概念 A

一、单选题（每题3分，共30分）(共10题；共30分)

1．（3分）（2022·兰州）如图， 内接于 ，CD是 的直径， ，则 （　　） 

A．70° B．60° C．50° D．40°

2．（3分）（2022·贵港）如图，⊙是的外接圆，是⊙的直径，点P在⊙上，若，则的度数是（　　）

A． B． C． D．

3．（3分）（2022·聊城）如图，AB，CD是的弦，延长AB，CD相交于点P．已知，，则的度数是（　　）

A．30° B．25° C．20° D．10°

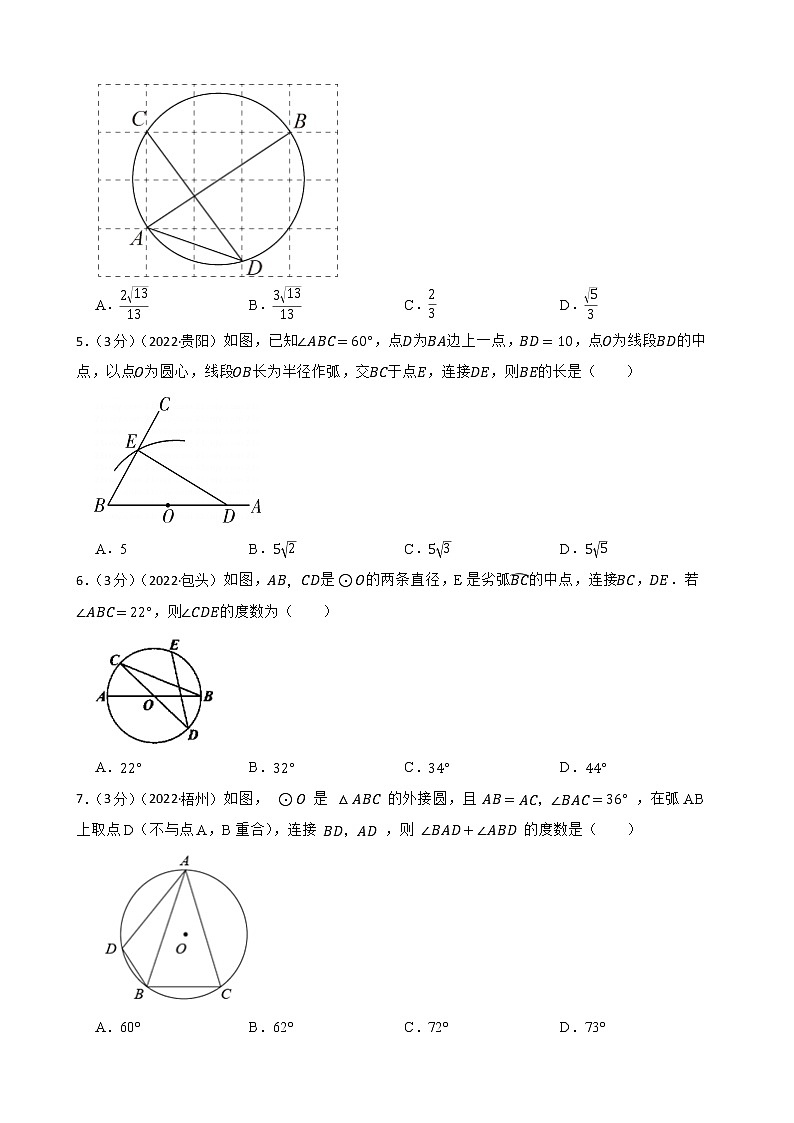
4．（3分）（2022·通辽）如图，由边长为1的小正方形构成的网格中，点，，都在格点上，以为直径的圆经过点，，则的值为（　　）

A． B． C． D．

5．（3分）（2022·贵阳）如图，已知，点为边上一点，，点为线段的中点，以点为圆心，线段长为半径作弧，交于点，连接，则的长是（　　）

A．5 B． C． D．

6．（3分）（2022·包头）如图，是的两条直径，E是劣弧的中点，连接，．若，则的度数为（　　）

A． B． C． D．

7．（3分）（2022·梧州）如图， 是 的外接圆，且 ，在弧AB上取点D（不与点A，B重合），连接 ，则 的度数是（　　）

A．60° B．62° C．72° D．73°

8．（3分）（2022·十堰）如图， 是等边 的外接圆，点 是弧 上一动点（不与 ， 重合），下列结论：① ；② ；③当 最长时， ；④ ，其中一定正确的结论有（　　）

A．1个 B．2个 C．3个 D．4个

9．（3分）（2022·山西）如图，内接于，AD是的直径，若，则的度数是（　　）

A．60° B．65° C．70° D．75°

10．（3分）（2022·宜昌）如图，四边形 内接于 ，连接 ， ， ，若 ，则 （　　） 

A． B． C． D．

二、填空题（每空3分，共18分）(共6题；共18分)

11．（3分）（2022·宁夏）如图，在中，半径垂直弦于点，若，，则　     　．

12．（3分）（2022·上海市）如图所示，小区内有个圆形花坛O，点C在弦AB上，AC=11，BC=21，OC=13，则这个花坛的面积为　     　．（结果保留）

13．（3分）（2022·锦州）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，∠ADC=130°，连接AC，则∠BAC的度数为　     　．

14．（3分）（2022·长沙）如图，A、B、C是上的点，，垂足为点D，且D为OC的中点，若，则BC的长为　     　.

15．（3分）（2022·龙东）如图，在中，AB是的弦，的半径为3cm，C为上一点，，则AB的长为　     　cm．

16．（3分）（2022·苏州）如图，AB是 的直径，弦CD交AB于点E，连接AC，AD.若 ，则 　     　° 

三、解答题（共8题，共72分）(共8题；共72分)

17．（8分）（2022·衢州）如图，C，D是以AB为直径的半圆上的两点，，连结BC，CD．

（1）（4分）求证：．

（2）（4分）若，，求阴影部分的面积．

18．（8分）（2022·六盘水）牂狗江“佘月郎山，西陵晚渡”的风景描绘中有半个月亮挂在山上，月亮之上有个“齐天大圣”守护洞口的传说．真实情况是老王山上有个月亮洞，洞顶上经常有猴子爬来爬去，下图是月亮洞的截面示意图．

（1）（4分）科考队测量出月亮洞的洞宽约是28m，洞高约是12m，通过计算截面所在圆的半径可以解释月亮洞像半个月亮，求半径的长（结果精确到0.1m）；

（2）（4分）若，点在上，求的度数，并用数学知识解释为什么“齐天大圣”点在洞顶上巡视时总能看清洞口的情况．

19．（8分）（2022·呼和浩特）如图，在中，，以为直径的⊙交于点，交线段的延长线于点，连接．

（1）（4分）求证：；

（2）（4分）若，，求．

20．（8分）（2022·威海）如图，四边形ABCD是⊙O的内接四边形，连接AC，BD，延长CD至点E．

（1）（4分）若AB＝AC，求证：∠ADB＝∠ADE；

（2）（4分）若BC＝3，⊙O的半径为2，求sin∠BAC．

21．（8分）（2022·铜仁）如图，D是以AB为直径的⊙O上一点，过点D的切线DE交AB的延长线于点E，过点B作BC⊥DE交AD的延长线于点C，垂足为点F.

（1）（4分）求证：AB=CB；

（2）（4分）若AB=18，sinA=，求EF的长.

22．（10分）（2022·黔东南）（1）（4分）请在图中作出的外接圆（尺规作图，保留作图痕迹，不写作法）；

（2）（6分）如图，是的外接圆，是的直径，点是的中点，过点的切线与的延长线交于点.

①求证：；

②若，，求的半径.

23．（10分）（2022·常州）（现有若干张相同的半圆形纸片，点是圆心，直径的长是，是半圆弧上的一点（点与点、不重合），连接、.

（1）（3分）沿、剪下，则是　     　三角形（填“锐角”、“直角”或“钝角”）；

（2）（3分）分别取半圆弧上的点、和直径上的点、.已知剪下的由这四个点顺次连接构成的四边形是一个边长为的菱形.请用直尺和圆规在图中作出一个符合条件的菱形（保留作图痕迹，不要求写作法）；

（3）（4分）经过数次探索，小明猜想，对于半圆弧上的任意一点，一定存在线段上的点、线段上的点和直径上的点、，使得由这四个点顺次连接构成的四边形是一个边长为的菱形.小明的猜想是否正确？请说明理由.

24．（12分）（2022·遵义）综合与实践

“善思”小组开展“探究四点共圆的条件”活动，得出结论：对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.

提出问题：

如图1，在线段同侧有两点B，D，连接，，，，如果，那么A，B，C，D四点在同一个圆上.

探究展示：

如图2，作经过点A，C，D的，在劣弧上取一点E（不与A，C重合），连接，则（依据1）

点A，B，C，E四点在同一个圆上（对角互补的四边形四个顶点共圆）

点B，D在点A，C，E所确定的上（依据2）

点A，B，C，E四点在同一个圆上

（1）（2分）反思归纳：上述探究过程中的“依据1”、“依据2”分别是指什么？

依据1：　                     　；依据2：　                             　.

（2）（3分）图3，在四边形中，，，则的度数为　     　.

（3）（5分）展探究：如图4，已知是等腰三角形，，点D在上（不与的中点重合），连接.作点C关于的对称点E，连接并延长交的延长线于F，连接，.

①求证：A，D，B，E四点共圆；

②若，的值是否会发生变化，若不变化，求出其值；若变化，请说明理由.

答案解析部分

1．【答案】C

2．【答案】C

3．【答案】C

4．【答案】B

5．【答案】A

6．【答案】C

7．【答案】C

8．【答案】C

9．【答案】C

10．【答案】B

11．【答案】

12．【答案】400π

13．【答案】40°

14．【答案】7

15．【答案】

16．【答案】62

17．【答案】（1）证明：∵ = ，

∴∠ACD＝∠DBA，

又 ∠CAB＝∠DBA，

∴∠CAB＝∠ACD，

∴ ；

（2）解：如图，连结OC，OD．

∵∠ACD＝30°，

∴∠ACD＝∠CAB＝30°，

∴∠AOD＝∠COB＝60°，

∴∠COD＝180°-∠AOD-∠COB＝60°．

∵ ，

∴S△DOC=S△DBC，

∴S阴影=S弓形COD+S△DOC=S弓形COD+S△DBC=S扇形COD，

∵AB＝4，

∴OA＝2，

∴S扇形COD= ，

∴S阴影= ．

18．【答案】（1）解： ， ， 

，

设半径为 ，则

在 中，

解得

答：半径 的长约为

（2）解：如图，在优弧 上任取一点 ，连接

，

，

，

因为CD在∠CMD的内部，所以点 在洞顶 上巡视时总能看清洞口 的情况．

19．【答案】（1）证明：连接AD，如图所示：

∵为⊙的直径，

∴AD⊥BC，

又∵，

∴三角形ABC为等腰三角形，

∴AD为BC的垂直平分线，

∴BD=CD．

（2）解：由（1）可得BD=CD=4，

，BC=2BD=8，

，

在Rt△ACD中，

，

又∵为⊙的直径，

∴∠BEC=∠ADC=90°，且∠C=∠C，

∴，

，即，

，

．

20．【答案】（1）解：∵圆内接四边形外角等于内对角，四边形ABCD是圆的内接四边形，

∴∠ABC＝∠ADE，

∵AB=AC，

∴∠ABC＝∠ACB，

∵∠ADB＝∠ACB，

∴∠ADB＝∠ADE．

（2）解：如图，作直径BF，连接FC，

则∠BCF=90°，

∵圆的半径为2，BC=3，

∴BF=4，BC=3，∠BAC= ∠BFC，

∴sin∠BAC= sin∠BFC=．

21．【答案】（1）证明：连接OD，如图1，

∵DE是⊙O的切线，

∴OD⊥DE.

∵BC⊥DE，

∴OD∥BC.

∴∠ODA=∠C.

∵OA=OD，

∴∠ODA=∠A.

∴∠A=∠C.

∴AB=BC；

（2）解：连接BD，则∠ADB=90°，如图2，

在Rt△ABD中，

∵sinA==，AB=18，

∴BD=6.

∵OB=OD，

∴∠ODB=∠OBD.

∵∠OBD+∠A=∠FDB+∠ODB=90°，

∴∠A=∠FDB.

∴sin∠A=sin∠FDB.

在Rt△BDF中，

∵sin∠BDF==，

∴BF=2.

由（1）知：OD∥BF，

∴△EBF∽△EOD.

∴=.即：=.

解得：BE=.

∴EF=.

22．【答案】（1）解：如下图所示

（2）解：①如下图所示，连接OC、OB

∵BD是的切线

∴

∵是对应的圆周角，是对应的圆心角

∴

∵点是的中点

∴

∴

∴

∴

∴

②如下图所示，连接CE

∵与是对应的圆周角

∴

∵是的直径

∴

∴

∴

∵

∴

∴的半径为.

23．【答案】（1）直角

（2）解：以A为圆心，AO为半径画弧交⊙O于点E，再以E为圆心，EO为半径画弧交于⊙O点F连接EF、FO、EA，G、H点分别与A、O点重合，即可，

作图如下：

由作图可知AE=EF=FH=HG=OA=AB=6，

即四边形EFHG是边长为6cm的菱形；

（3）解：小明的猜想正确，理由如下：
如图2中，设CM=，CN=CB，取AP=BQ=4cm，

则∵，
∴MN∥AB，
∴，
∴MN=PQ=4，
∴四边形MNQP是平行四边形，
∵，
∴MP∥CO，
∴，
∴PM=4cm，
∴MN=4cm，
∴四边形MNQP是菱形，边长为4cm，
∴小明的猜想正确.

24．【答案】（1）圆内接四边形对角互补；同圆中，同弧所对的圆周角相等

（2）45°

（3）解：①，

，

点与点关于对称，

，

，

四点共圆；

②，理由如下，

如图，四点共圆，

，

关于对称，

，

，

，

，

，

，

，

又，

，

，

，

，

.