第15讲 圆的认识、周长与面积（基础版）小升初数学精讲精练专题真题汇编讲义（原卷+解析）通用版

基础版（通用）

小升初数学精讲精练专题汇编讲义

第15讲 圆的认识、周长与面积

知识点一：圆的认识

1.在同圆或等圆中,所有的直径都相等,所有的半径都相等。 

2.圆是轴对称图形,圆有无数条对称轴,圆的对称轴就是直径所在的直线。

知识点二：圆的周长和面积

1.圆的周长

(1)圆周率:圆的周长与直径的比值叫作圆周率。圆周率用希腊字母“π”表示,它是一个无限不循环 小数。经过精密计算:π=3.1415926…在小学数学中,我们常常取圆周率的近似值3.14

(2)圆的周长=圆周率×直径或圆周率×半径×2　用字母表示为:C=πd或2πr　

2.圆的面积:把一个圆平均分成若干份,剪开后拼成一个近似的平行四边形,如果分的份数越多,拼成的图形越接近长方形,这个近似长方形的长等于圆周长的一半,宽等于圆的半径 ,由此圆的面积S=πr2　

3.圆环的面积

(1)同一个圆心的两个半径不相等的圆,它们之间的部分叫作　圆环　

(2)面积公式:　S=πR2-πr2　

知识点三：组合图形的面积

1.求组合图形面积的方法。

(1)分割法:把阴影部分分割成几个基本图形,利用求几个基本图形面积的　和　求出阴影部分的面积。　

(2)添补法:在阴影部分上添补一个基本图形,使其变成另一个基本图形,计算出这个基本图形的面积后　减去　补上的基本图形的面积,从而求出阴影部分的面积。

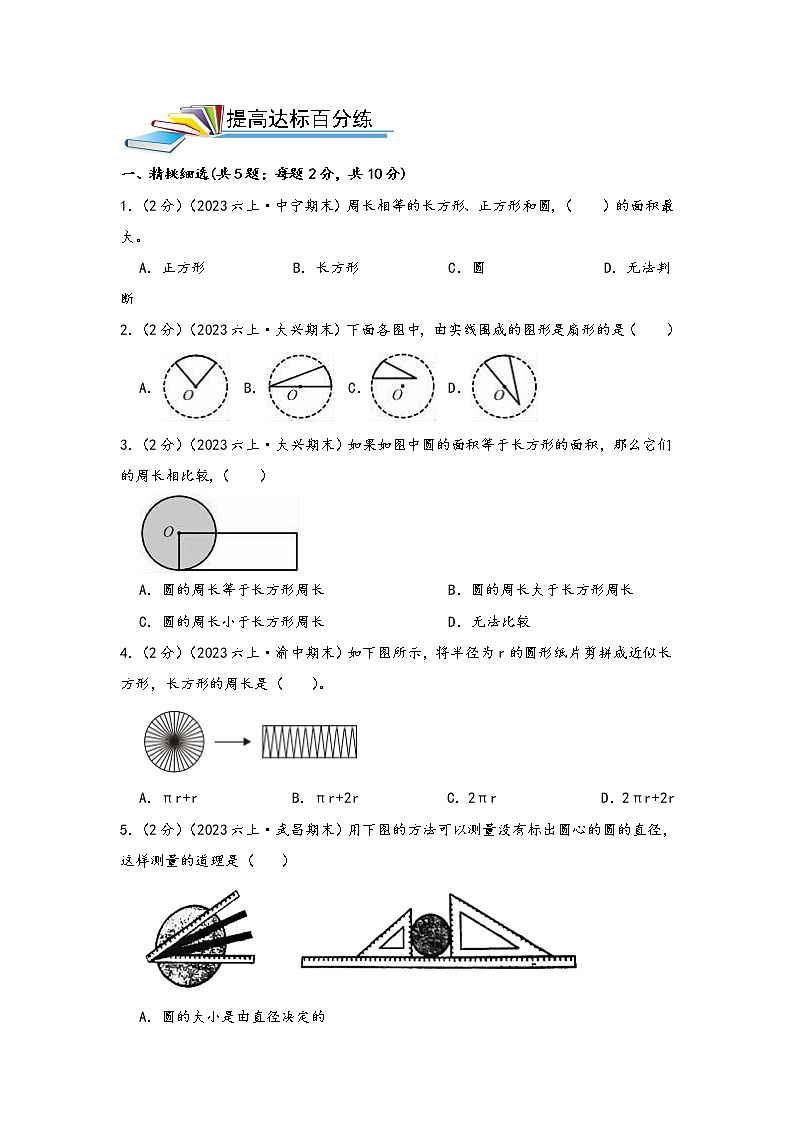
一、精挑细选(共5题；每题2分，共10分)

1．（2分）（2023六上·中宁期末）周长相等的长方形、正方形和圆，（　　）的面积最大。 

A．正方形 B．长方形 C．圆 D．无法判断

【答案】C

【规范解答】解：周长相等的长方形、正方形和圆，圆的面积最大。
故答案为：C。

【思路点拨】当周长相等时，形状越近似于圆，面积越大，其中圆的面积最大。

2．（2分）（2023六上·大兴期末）下面各图中，由实线围成的图形是扇形的是（　　）

A．  B．C． D．

【答案】A

【规范解答】只有中由实线围成的图形是扇形。
故答案为：A。
【思路点拨】一条圆弧和经过这条圆弧两端的两条半径所围成的图形叫扇形（半圆与直径的组合也是扇形），据此解答。

3．（2分）（2023六上·大兴期末）如果如图中圆的面积等于长方形的面积，那么它们的周长相比较，（　　）

A．圆的周长等于长方形周长 B．圆的周长大于长方形周长

C．圆的周长小于长方形周长 D．无法比较

【答案】C

【规范解答】 圆的面积为πr2。圆的面积=长方形面积，由图可知，长方形的宽为圆的半径r，所以长方形长为：πr2÷r=πr。所以圆的周长为：2πr；长方形的周长为：2(πr+r)=2πr+2r。2πr+2r>2πr，所以圆与长方形的周长相比， 圆的周长小于长方形周长 。
故答案为：C。
【思路点拨】圆的面积=π×半径2；圆的周长=2×半径×π；长方形周长=2×（长+宽）；长方形面积=长×宽，据此解答。

4．（2分）（2023六上·渝中期末）如下图所示，将半径为r的圆形纸片剪拼成近似长方形，长方形的周长是（　　）。

A．πr+r B．πr+2r C．2πr D．2πr+2r

【答案】D

【规范解答】解：长方形的周长是2πr+2r。
故答案为：D。
【思路点拨】拼成的近似长方形的长是圆周长的一半，宽是圆的半径。所以拼成的这个长方形的周长就是圆周长加上两条半径的长度。圆周长是2πr，两条半径的长度是2r，那么长方形的周长就是2πr+2r。

5．（2分）（2023六上·武昌期末）用下图的方法可以测量没有标出圆心的圆的直径，这样测量的道理是（　　）

A．圆的大小是由直径决定的

B．一个圆内有无数条直径

C．同一圆内，直径的长度是半径的2倍

D．直径是圆内最长的线段

【答案】D

【规范解答】解：这样测量的道理是：直径是圆内最长的线段。
故答案为：D。
【思路点拨】在同一个圆内有无数条直径，直径是圆内最长的线段。

二、判断正误(共5题；每题1分，共5分)

6．（1分）（2023六上·北碚期末）一个圆的半径缩小到原来的，则它的面积也缩小到原来的。（　　）

【答案】（1）错误

【规范解答】解：×=。
故答案为：错误。

【思路点拨】圆的面积=π×半径2，一个圆的半径缩小到原来的，则它的面积缩小到原来的。

7．（1分）（2023六上·茂南期末）圆的直径扩大到原来的3倍，周长和面积也扩大到原来的3倍。（    ）

【答案】（1）错误

【规范解答】解：圆的直径扩大到原来的3倍，周长也扩大3倍，面积也扩大到原来的9倍。原题说法错误。
故答案为：错误。

【思路点拨】C=2πr=πd，S=πr2，所以圆周长和直径扩大的倍数相同，圆面积扩大的倍数是直径扩大倍数的平方倍。

8．（1分）（2023六上·即墨期末）两个圆周长的比是1∶2，它们面积的比是1∶4。（　　）

【答案】（1）正确

【规范解答】解：两个圆周长的比是1∶2，它们面积的比是1∶4。原题说法正确。
故答案为：正确。

【思路点拨】两个圆的半径比、直径比、周长比都相同；两个圆的面积比是半径、直径或周长平方的比。

9．（1分）（2022六上·龙里月考）半径是3厘米的圆比直径是4厘米的圆小。（　　）

【答案】（1）错误

【规范解答】解：4÷2=2厘米，所以半径是3厘米的圆比直径是4厘米的圆大。
故答案为：错误。
【思路点拨】圆的半径=圆的直径÷2；
半径越大，圆就越大。

10．（1分）（2022六上·雷州月考）用50.24厘米绳子分别围成一个最大的圆、长方形和正方形，圆的面积最大。（　　）

【答案】（1）正确

【规范解答】解：用50.24厘米绳子分别围成一个最大的圆、长方形和正方形，圆的面积最大，原题干说法正确。
故答案为：正确。
【思路点拨】周长相等的长方形、正方形和圆，圆的面积最大。

三、仔细想，认真填(共9题；每空1分，共15分)

11．（1分）（2023六上·北碚期末）张叔叔驾驶轿车用时3分钟匀速经过一座大桥，轿车轮胎的外直径是0.7m，匀速行使时轮胎每分钟大约转动500圈，这座大桥大约长　     　m。

【答案】3297

【规范解答】解：3.14×0.7×500×3
=2.198×500×3
=1099×3
=3297（米）。
故答案为：3297。

【思路点拨】这座大桥大约的长度=轿车轮胎的周长×平均每分钟转动的圈数×行驶的时间，其中，轿车轮胎的周长=π×直径。

12．（1分）（2023六上·大兴期末）如图中两个圆的直径分别是8厘米和6厘米，阴影部分的面积是　     　厘米2。

【答案】21.98

【规范解答】（8÷2）2×3.14-（6÷2）2×3.14
=42×3.14-32×3.14
=16×3.14-9×3.14
=50.24-28.26
=21.98（厘米2）
故答案为：21.98。

【思路点拨】圆的面积=半径2×π，据此解答。

13．（2分）（2023六上·大兴期末）一个圆的半径是5厘米，它的周长是　     　厘米，面积是　     　平方厘米。

【答案】31.4；78.5

【规范解答】2×5×3.14=10×3.14=31.4（厘米）；
52×3.14=25×3.14=78.5（平方厘米）。
故答案为：31.4，78.5。

【思路点拨】圆的周长=2×半径×π；圆的面积=半径2×π，据此解答。

14．（2分）（2023六上·渝中期末）欣欣用右面的方法测出一元硬币的直径是　     　cm，然后让一元硬币在直尺上滚动一周的长度是　     　cm。

【答案】2.5；7.85

【规范解答】解：直径是2.5cm，滚动一周的长度：3.14×2.5=7.85（cm）。
故答案为：2.5；7.85。
【思路点拨】左右两个竖着的直尺对应的刻度之间的数值就是硬币的直径。用直径乘3.14即可求出它的周长，也就是一元硬币在直尺上滚动一周的长度。

15．（1分）（2023六上·武昌期末）有一个环形铁片，如右图所示：它的外圆半径是5厘米，内圆半径是3厘米，这个环形铁片的面积是　     　平方厘米。

【答案】50.24

【规范解答】解：3.14×（52-32）
=3.14×（25-9）
=3.14×16
=50.24（平方厘米）。
故答案为：50.24。

【思路点拨】这个环形铁片的面积=π×（R2-r2）。

16．（2分）（2023六上·武昌期末）如下图，图中A、B两点之间的部分叫　     　，读作　     　。

【答案】弧；弧AB

【规范解答】解：图中A、B两点之间的部分叫弧，读作弧AB。
故答案为：弧；弧AB。

【思路点拨】圆上任意两点间的部分叫做圆弧，简称弧。

17．（2分）（2023六上·武昌期末） 用圆规画圆时，如果圆规的两脚叉开2cm，则画出的圆的面积是　     　cm2；如果画出的圆的周长是18.84cm，则这个圆的面积是　     　cm2。

【答案】12.56；28.26

【规范解答】解：3.14×22
=3.14×4
=12.56（平方厘米）
18.84÷3.14÷2
=6÷2
=3（厘米）
3.14×32
=3.14×9
=28.26（平方厘米）。
故答案为：12.56；28.26。

【思路点拨】圆规两脚叉开的距离=圆的半径；圆的面积=π×半径2。

18．（1分）（2023六上·富县期末）一种电动车轮胎滚动一周前进的距离是18.84分米，这种轮胎的外直径是　     　分米。

【答案】6

【规范解答】解：18.84÷3.14=6（分米）
故答案为：6。

【思路点拨】圆的周长÷π=圆的直径。

19．（3分）（2023六上·宽城期末）把一个半径是2cm的圆等分成若干份，剪开后拼成近似的平行四边形，这个平行四边形的底是　     　cm，高是　     　cm，所以这个圆的面积是　     　cm2。

【答案】6.28；2；12.56

【规范解答】解：底：3.14×2=6.28（厘米）
高：2厘米
面积：3.14×2×2=12.56（平方厘米）
故答案为：6.28；2；12.56。

【思路点拨】平行四边形的底是圆周长的一半，高是圆的半径，圆的面积=π×半径的平方。

四、巧妙作图(共2题；共20分)

20．（10分）（2023六上·武昌期末）六位同学参加趣味“套圈”比赛，场地设计如下：

（1）（5分）这样设计比赛场地公平吗？理由是：

（2）（5分）请在示意图中画出你认为公平的“套圈”比赛场地。

【答案】（1）解：这样设计比赛场地不公平，因为③、④距离瓶子近，其余距离瓶子远。

（2）解：

【思路点拨】（1）场地设计的六处地方离瓶子的距离不相等，所以设计比赛场地不公平；
（2）圆上到圆心的距离都相等，所以设计成圆形是公平的。

21．（10分）（2023六上·香洲期末）下面一个小方格边长是1cm，请在方格图里按要求画图。

（1）（5分）画出圆心在（5，4），半径另一端在（7，4）的圆；

（2）（5分）在画出的圆中画一个圆心角是100°的扇形：

【答案】（1）解：

（2）解：

【思路点拨】（1）用数对表示位置时，前面一个数表示第几列，后面一个数表示第几行；列数一般从左往右数，行数一般从前往后数；以（5，4）为圆心，半径为2厘米画圆；
（2）以画出的圆的圆心为扇形的顶点，画出扇形。

五、计算能手(共2题；共10分)

22．（5分）（2020·慈溪）如图正方形AOBC中，点O是圆心，求阴影部分的面积．（单位：厘米）

【答案】解：（4+4×2）×4÷2﹣4×4÷2﹣ ×3.14×42

＝24﹣8﹣12.56

＝3.44（平方厘米）

答：阴影部分的面积是3.44平方厘米．

【思路点拨】因为右边的三角形是等腰三角形，所以BC=4，所以阴影部分的面积=正方形的面积-圆的面积，其中正方形的面积=边长×边长，圆的面积=πr2。

23．（5分）（2020·南关模拟）求图中阴影部分的面积之和。（单位：cm）

【答案】解：4×（4÷2）

＝4×2

＝8（平方厘米）

答：阴影部分的面积之和为8平方厘米。

【思路点拨】如图：把下面的阴影部分分别移动到红色部分，则阴影部分的面积实际就是一个长方形的面积，长是4厘米，宽是2厘米，根据长方形面积公式计算阴影部分的总面积即可。
 

六、解答问题(共8题；共40分)

24．（5分）（2023六上·番禺期末）一匹马拴在树上，绳长4m，求这匹马走一圈是多少米？最多能吃到多大面积的草？

【答案】解：4×2×3.14
=8×3.14
=25.12（米）
3.14×42
=3.14×16
=50.24（平方米）
答：这匹马走一圈是25.12米，最多能吃到50.24平方米的草。

【思路点拨】这匹马走一圈的路程=绳子的长度×2×π，最多能吃到草的面积=π×绳子长度2。

25．（5分）（2023六上·武汉期末）如图，一个花坛的中间是边长为5米的正方形，四周是四个完全一样的半圆形，这个花坛的周长和面积各是多少？

【答案】解：周长：3.14×5×2=31.4（米）
面积：5×5+3.14×（5÷2）2×2
=25+3.14×6.25×2
=25+39.25
=64.25（平方米）
答：这个花坛的周长是31.4米，面积是64.25平方米。

【思路点拨】这个花坛的周长是两个直径5米的圆的周长。面积是两个圆的面积加上中间正方形的面积。

26．（5分）（2023六上·武汉期末）公园准备将原来直径为10米的半圆形景观鱼池进行扩建，把半径增加1米，扩建后景观鱼池的面积增加了多少平方米？

【答案】解：10÷2=5（米），5+1=6（米）
3.14×（62-52）÷2
=3.14×（36-25）÷2
=3.14×11÷2
=17.27（平方米）
答：扩建后景观鱼池的面积增加了17.27平方米。

【思路点拨】增加的面积是一个半圆环的面积。用内圆直径除以2求出内圆半径，用内圆半径加上1米求出外圆半径。然后根据圆环面积公式计算即可。圆环的面积公式：S=π（R2-r2）。

27．（5分）（2023六上·渝中期末）张红家一扇门上要装上形状如下图所示的装饰木条，需要木条多少米？

【答案】解：2+2+1.2+3.14×1.2÷2
=5.2+1.884
=7.084（米）
答：需要木条7.084米。

【思路点拨】需要木条的长度是两条长2米的，一条长1.2米的，还有一条直径是1.2米的圆周长的一半。把这几部分长度相加即可。

28．（5分）（2023六上·富县期末）在铅球比赛中，铅球投掷的落点区域是圆（如图），超超最远投掷距离为12米，铅球可能的落点区域面积是多少平方米？

【答案】解：3.14×12×12×
=3.14×144×
=452.16×
=113.04（平方米）
答：铅球可能的落点区域面积是113.04平方米。

【思路点拨】S=π×半径的平方，据此求出圆的面积，圆的面积×=铅球可能的落点区域面积。

29．（5分）小明沿6米长的路走了3次，第一次10步走完，第二次9步走完，第三次11步走完，他平均一步的长度是多少米?他沿着一个圆形花坛走了一圈，刚好是157步。这个花坛的面积约是多少平方米?( 值取3.14)

【答案】解：6×3÷(10+9+11)=0.6(米)

157×0.6=94.2(米)

94.2÷3.14÷2=15(米)

152×3.14=706.5(平方米)

【规范解答】平均一步的长度：
6×3÷（10+9+11）
=6×3÷30
=18÷30
=0.6（米）；
圆形花坛的周长：157×0.6=94.2（米）；
圆的半径：
94.2÷3.14÷2
=30÷2
=15（米）；
圆形花坛的面积：
3.14×152
=3.14×225
=706.5（平方米）.
答：他平均一步的长度是0.6米，这个花坛的面积约是706.5平方米.
【思路点拨】根据题意，先求出三次一共走了多少米，用路的长度×走的次数=一共走的米数，再求出三次一共走了几步，将三次走的步数相加即可，最后用总米数÷总步数=平均每步的长度，据此列式解答；
根据条件“ 他沿着一个圆形花坛走了一圈，刚好是157步 ”可知，用每步的长度×步数=这个圆形花坛的周长，然后用圆的周长÷π÷2=圆的半径，最后用圆的面积公式：S=πr2，据此列式解答.

30．（5分）（2018六上·龙岗期中）一辆自行车的外轮胎直径是50厘米，如果每分钟转100周，要过一座942米长的桥，需要多少分钟?

【答案】解：3.14×50×100=15700（厘米/分钟）=157（米/分钟）
942÷157=6（分钟）
答：需要6分钟。

【思路点拨】圆的周长：C=πd，时间=路程÷速度。

31．（5分）（2018六上·龙岗期中）一个圆形花坛的周长是31.4米(如图)，在它的外围铺一条2米宽的环形小路(阴影部分)，这条小路的面积是多少平方米?

【答案】解：花坛半径：31.4÷3.14÷2=5米，大圆半径：5+2=7米，圆环面积：3.14×（72-52）=3.14×24=75.36平方米。
答：这条小路的面积是75.36平方米。

【思路点拨】圆环的面积=π×（R2-r2）。