10-等差数列-五年2018-2022高考数学真题按知识点分类汇编

这是一份10-等差数列-五年2018-2022高考数学真题按知识点分类汇编，共34页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
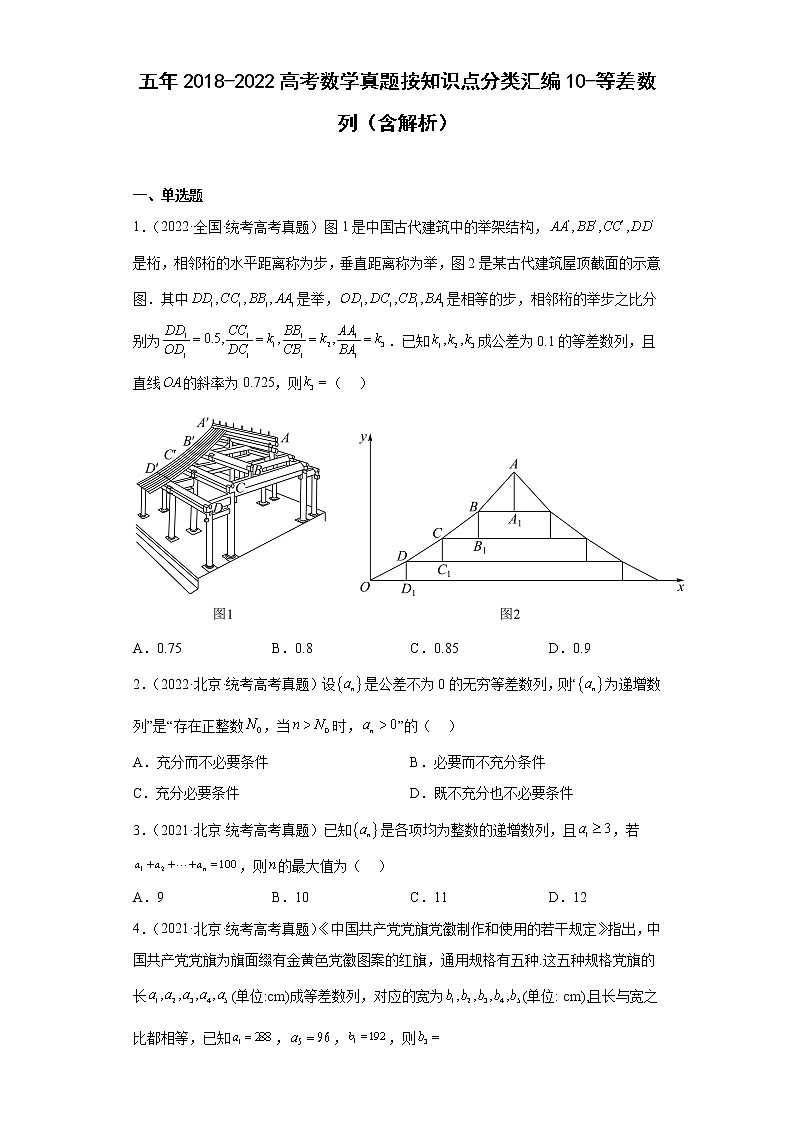
1．（2022·全国·统考高考真题）图1是中国古代建筑中的举架结构，是桁，相邻桁的水平距离称为步，垂直距离称为举，图2是某古代建筑屋顶截面的示意图．其中是举，是相等的步，相邻桁的举步之比分别为．已知成公差为0.1的等差数列，且直线的斜率为0.725，则（ ）
A．0.75B．0.8C．0.85D．0.9
2．（2022·北京·统考高考真题）设是公差不为0的无穷等差数列，则“为递增数列”是“存在正整数，当时，”的（ ）
A．充分而不必要条件B．必要而不充分条件
C．充分必要条件D．既不充分也不必要条件
3．（2021·北京·统考高考真题）已知是各项均为整数的递增数列，且，若，则的最大值为（ ）
A．9B．10C．11D．12
4．（2021·北京·统考高考真题）《中国共产党党旗党徽制作和使用的若干规定》指出，中国共产党党旗为旗面缀有金黄色党徽图案的红旗，通用规格有五种.这五种规格党旗的长(单位:cm)成等差数列，对应的宽为(单位: cm),且长与宽之比都相等，已知，，，则
A．64B．96C．128D．160
5．（2020·全国·统考高考真题）北京天坛的圜丘坛为古代祭天的场所，分上、中、下三层，上层中心有一块圆形石板(称为天心石)，环绕天心石砌9块扇面形石板构成第一环，向外每环依次增加9块，下一层的第一环比上一层的最后一环多9块，向外每环依次也增加9块，已知每层环数相同，且下层比中层多729块，则三层共有扇面形石板(不含天心石)（ ）
A．3699块B．3474块C．3402块D．3339块
6．（2020·浙江·统考高考真题）已知等差数列{an}的前n项和Sn，公差d≠0，．记b1=S2，bn+1=S2n+2–S2n，，下列等式不可能成立的是（ ）
A．2a4=a2+a6B．2b4=b2+b6C．D．
7．（2019·全国·高考真题）记为等差数列的前n项和．已知，则
A．B．C．D．
8．（2018·全国·高考真题）设为等差数列的前项和，若，，则
A．B．C．D．
二、填空题
9．（2022·全国·统考高考真题）记为等差数列的前n项和．若，则公差_______．
10．（2020·全国·统考高考真题）记为等差数列的前n项和．若，则__________．
11．（2020·海南·高考真题）将数列{2n–1}与{3n–2}的公共项从小到大排列得到数列{an}，则{an}的前n项和为________．
12．（2019·全国·统考高考真题）记Sn为等差数列{an}的前n项和，，则___________.
13．（2019·全国·高考真题）记为等差数列的前项和，若，则___________.
三、解答题
14．（2022·全国·统考高考真题）记为数列的前n项和，已知是公差为的等差数列．
(1)求的通项公式；
(2)证明：．
15．（2022·全国·统考高考真题）记为数列的前n项和．已知．
(1)证明：是等差数列；
(2)若成等比数列，求的最小值．
16．（2022·全国·统考高考真题）已知为等差数列，是公比为2的等比数列，且．
(1)证明：；
(2)求集合中元素个数．
17．（2022·浙江·统考高考真题）已知等差数列的首项，公差．记的前n项和为．
(1)若，求；
(2)若对于每个，存在实数，使成等比数列，求d的取值范围．
18．（2022·天津·统考高考真题）设是等差数列，是等比数列，且．
(1)求与的通项公式；
(2)设的前n项和为，求证：；
(3)求．
19．（2021·全国·统考高考真题）记为数列的前n项和，为数列的前n项积，已知．
（1）证明：数列是等差数列;
（2）求的通项公式．
20．（2021·全国·统考高考真题）记是公差不为0的等差数列的前n项和，若．
（1）求数列的通项公式；
（2）求使成立的n的最小值．
21．（2021·全国·统考高考真题）设是首项为1的等比数列，数列满足．已知，，成等差数列．
（1）求和的通项公式；
（2）记和分别为和的前n项和．证明：．
22．（2021·全国·统考高考真题）已知数列的各项均为正数，记为的前n项和，从下面①②③中选取两个作为条件，证明另外一个成立．
①数列是等差数列：②数列是等差数列；③．
注：若选择不同的组合分别解答，则按第一个解答计分．
23．（2021·全国·统考高考真题）已知数列满足，
（1）记，写出，，并求数列的通项公式；
（2）求的前20项和.
24．（2021·全国·高考真题）记为数列的前n项和，已知，且数列是等差数列，证明：是等差数列.
25．（2021·天津·统考高考真题）已知是公差为2的等差数列，其前8项和为64．是公比大于0的等比数列，．
（I）求和的通项公式；
（II）记，
（i）证明是等比数列；
（ii）证明
26．（2020·天津·统考高考真题）已知为等差数列，为等比数列，．
（Ⅰ）求和的通项公式；
（Ⅱ）记的前项和为，求证：；
（Ⅲ）对任意的正整数，设求数列的前项和．
27．（2020·山东·统考高考真题）某男子擅长走路，9天共走了1260里，其中第1天、第4天、第7天所走的路程之和为390里.若从第2天起，每天比前一天多走的路程相同，问该男子第5天走多少里.这是我国古代数学专著《九章算术》中的一个问题，请尝试解决.
28．（2018·全国·高考真题）记为等差数列的前项和，已知，．
（1）求的通项公式；
（2）求，并求的最小值．
29．（2019·全国·高考真题）已知数列{an}和{bn}满足a1=1，b1=0， ，.
（1）证明：{an+bn}是等比数列，{an–bn}是等差数列；
（2）求{an}和{bn}的通项公式.
30．（2019·全国·高考真题）记Sn为等差数列{an}的前n项和，已知S9=－a5．
（1）若a3=4，求{an}的通项公式；
（2）若a1>0，求使得Sn≥an的n的取值范围．
31．（2019·全国·高考真题）已知是各项均为正数的等比数列，.
（1）求的通项公式；
（2）设，求数列的前n项和.
参考答案：
1．D
【分析】设，则可得关于的方程，求出其解后可得正确的选项.
【详解】设，则，
依题意，有，且，
所以，故，
故选：D
2．C
【分析】设等差数列的公差为，则，利用等差数列的通项公式结合充分条件、必要条件的定义判断可得出结论.
【详解】设等差数列的公差为，则，记为不超过的最大整数.
若为单调递增数列，则，
若，则当时，；若，则，
由可得，取，则当时，，
所以，“是递增数列”“存在正整数，当时，”；
若存在正整数，当时，，取且，，
假设，令可得，且，
当时，，与题设矛盾，假设不成立，则，即数列是递增数列.
所以，“是递增数列”“存在正整数，当时，”.
所以，“是递增数列”是“存在正整数，当时，”的充分必要条件.
故选：C.
3．C
【分析】使数列首项、递增幅度均最小，结合等差数列的通项及求和公式求得可能的最大值，然后构造数列满足条件，即得到的最大值．
【详解】若要使n尽可能的大，则，递增幅度要尽可能小，
不妨设数列是首项为3，公差为1的等差数列，其前n项和为，
则，，
所以.
对于，，
取数列各项为(，,
则，
所以n的最大值为11．
故选：C．
4．C
【分析】设等差数列公差为，求得，得到，结合党旗长与宽之比都相等和，列出方程，即可求解.
【详解】由题意，五种规格党旗的长(单位:cm)成等差数列，设公差为，
因为，，可得，
可得，
又由长与宽之比都相等，且，可得，所以.
故选：C.
5．C
【分析】第n环天石心块数为，第一层共有n环，则是以9为首项，9为公差的等差数列，
设为的前n项和，由题意可得，解方程即可得到n，进一步得到.
【详解】设第n环天石心块数为，第一层共有n环，
则是以9为首项，9为公差的等差数列，，
设为的前n项和，则第一层、第二层、第三层的块数分
别为，因为下层比中层多729块，
所以，
即
即，解得，
所以.
故选：C
【点晴】本题主要考查等差数列前n项和有关的计算问题，考查学生数学运算能力，是一道容易题.
6．D
【分析】根据题意可得，，而，即可表示出题中，再结合等差数列的性质即可判断各等式是否成立．
【详解】对于A，因为数列为等差数列，所以根据等差数列的下标和性质，由可得，，A正确；
对于B，由题意可知，，，
∴，，，．
∴，．
根据等差数列的下标和性质，由可得，B正确；
对于C，，
当时，，C正确；
对于D，，，
．
当时，，∴即；
当时，，∴即，所以，D不正确．
故选：D.
【点睛】本题主要考查等差数列的性质应用，属于基础题．
7．A
【分析】等差数列通项公式与前n项和公式．本题还可用排除，对B，，，排除B，对C，，排除C．对D，，排除D，故选A．
【详解】由题知，，解得，∴，故选A．
【点睛】本题主要考查等差数列通项公式与前n项和公式，渗透方程思想与数学计算等素养．利用等差数列通项公式与前n项公式即可列出关于首项与公差的方程，解出首项与公差，在适当计算即可做了判断．
8．B
【详解】分析：首先设出等差数列的公差为，利用等差数列的求和公式，得到公差所满足的等量关系式，从而求得结果，之后应用等差数列的通项公式求得，从而求得正确结果.
详解：设该等差数列的公差为，
根据题中的条件可得，
整理解得，所以，故选B.
点睛：该题考查的是有关等差数列的求和公式和通项公式的应用，在解题的过程中，需要利用题中的条件，结合等差数列的求和公式，得到公差的值，之后利用等差数列的通项公式得到与的关系，从而求得结果.
9．2
【分析】转化条件为，即可得解.
【详解】由可得，化简得，
即，解得.
故答案为：2.
10．
【分析】因为是等差数列，根据已知条件，求出公差，根据等差数列前项和，即可求得答案.
【详解】是等差数列，且，
设等差数列的公差
根据等差数列通项公式：
可得
即：
整理可得：
解得：
根据等差数列前项和公式：
可得：
.
故答案为：.
【点睛】本题主要考查了求等差数列的前项和，解题关键是掌握等差数列的前项和公式，考查了分析能力和计算能力，属于基础题.
11．
【分析】首先判断出数列与项的特征，从而判断出两个数列公共项所构成新数列的首项以及公差，利用等差数列的求和公式求得结果.
【详解】因为数列是以1为首项，以2为公差的等差数列，
数列是以1首项，以3为公差的等差数列，
所以这两个数列的公共项所构成的新数列是以1为首项，以6为公差的等差数列，
所以的前项和为，
故答案为：.
【点睛】该题考查的是有关数列的问题，涉及到的知识点有两个等差数列的公共项构成新数列的特征，等差数列求和公式，属于简单题目.
12．4.
【分析】根据已知求出和的关系，再结合等差数列前n项和公式求得结果.
【详解】因，所以，即，
所以．
【点睛】本题主要考查等差数列的性质、基本量的计算．渗透了数学运算素养．使用转化思想得出答案．
13．100
【分析】根据题意可求出首项和公差，进而求得结果.
【详解】得
【点睛】本题考点为等差数列的求和，为基础题目，利用基本量思想解题即可，充分记牢等差数列的求和公式是解题的关键．
14．(1)
(2)见解析
【分析】（1）利用等差数列的通项公式求得，得到，利用和与项的关系得到当时，,进而得：，利用累乘法求得，检验对于也成立，得到的通项公式；
（2）由（1）的结论，利用裂项求和法得到，进而证得.
【详解】（1）∵，∴,∴,
又∵是公差为的等差数列，
∴,∴,
∴当时，，
∴,
整理得：,
即,
∴
，
显然对于也成立，
∴的通项公式；
（2）
∴
15．(1)证明见解析；
(2)．
【分析】（1）依题意可得，根据，作差即可得到，从而得证；
（2）法一：由（1）及等比中项的性质求出，即可得到的通项公式与前项和，再根据二次函数的性质计算可得．
【详解】（1）因为，即①，
当时，②，
①②得，，
即，
即，所以，且，
所以是以为公差的等差数列．
（2）[方法一]：二次函数的性质
由（1）可得，，，
又，，成等比数列，所以，
即，解得，
所以，所以，
所以，当或时，．
[方法二]：【最优解】邻项变号法
由（1）可得，，，
又，，成等比数列，所以，
即，解得，
所以，即有.
则当或时，．
【整体点评】（2）法一：根据二次函数的性质求出的最小值，适用于可以求出的表达式；
法二：根据邻项变号法求最值，计算量小，是该题的最优解．
16．(1)证明见解析；
(2)．
【分析】（1）设数列的公差为，根据题意列出方程组即可证出；
（2）根据题意化简可得，即可解出．
【详解】（1）设数列的公差为，所以，，即可解得，，所以原命题得证．
（2）由（1）知，，所以，即，亦即，解得，所以满足等式的解，故集合中的元素个数为．
17．(1)
(2)
【分析】（1）利用等差数列通项公式及前项和公式化简条件，求出，再求；
(2)由等比数列定义列方程，结合一元二次方程有解的条件求的范围.
【详解】（1）因为，
所以，
所以，又，
所以，
所以，
所以，
（2）因为，，成等比数列，
所以，
，
，
由已知方程的判别式大于等于0，
所以，
所以对于任意的恒成立，
所以对于任意的恒成立，
当时，，
当时，由，可得
当时，，
又
所以
18．(1)
(2)证明见解析
(3)
【分析】（1）利用等差等比数列的通项公式进行基本量运算即可得解；
（2）由等比数列的性质及通项与前n项和的关系结合分析法即可得证；
（3）先求得，进而由并项求和可得，再结合错位相减法可得解.
【详解】（1）设公差为d，公比为，则，
由可得（舍去），
所以；
（2）证明：因为所以要证，
即证，即证，
即证，
而显然成立，所以；
（3）因为
，
所以
，
设
所以，
则，
作差得
，
所以，
所以.
19．（1）证明见解析；（2）.
【分析】（1）由已知得,且，取,得,由题意得,消积得到项的递推关系,进而证明数列是等差数列;
（2）由（1）可得的表达式,由此得到的表达式,然后利用和与项的关系求得.
【详解】（1）[方法一]：
由已知得,且，,
取,由得,
由于为数列的前n项积，
所以,
所以，
所以,
由于
所以，即,其中
所以数列是以为首项，以为公差等差数列;
[方法二]【最优解】：
由已知条件知 ①
于是． ②
由①②得． ③
又， ④
由③④得．
令，由，得．
所以数列是以为首项，为公差的等差数列．
[方法三]：
由，得，且，，．
又因为，所以，所以．
在中，当时，．
故数列是以为首项，为公差的等差数列．
[方法四]：数学归纳法
由已知，得，，，，猜想数列是以为首项，为公差的等差数列，且．
下面用数学归纳法证明．
当时显然成立．
假设当时成立，即．
那么当时，．
综上，猜想对任意的都成立．
即数列是以为首项，为公差的等差数列．
（2）
由（1）可得，数列是以为首项，以为公差的等差数列，
,
,
当n=1时，,
当n≥2时,,显然对于n=1不成立,
∴.
【整体点评】（1）方法一从得，然后利用的定义，得到数列的递推关系，进而替换相除消项得到相邻两项的关系，从而证得结论；
方法二先从的定义，替换相除得到，再结合得到，从而证得结论，为最优解；
方法三由，得，由的定义得，进而作差证得结论；方法四利用归纳猜想得到数列，然后利用数学归纳法证得结论．
（2）由（1）的结论得到，求得的表达式,然后利用和与项的关系求得的通项公式；
20．(1)；(2)7.
【分析】(1)由题意首先求得的值，然后结合题意求得数列的公差即可确定数列的通项公式；
(2)首先求得前n项和的表达式，然后求解二次不等式即可确定n的最小值.
【详解】(1)由等差数列的性质可得：，则：，
设等差数列的公差为，从而有：，
，
从而：，由于公差不为零，故：，
数列的通项公式为：.
(2)由数列的通项公式可得：，则：，
则不等式即：，整理可得：，
解得：或，又为正整数，故的最小值为.
【点睛】等差数列基本量的求解是等差数列中的一类基本问题，解决这类问题的关键在于熟练掌握等差数列的有关公式并能灵活运用.
21．（1），；（2）证明见解析.
【分析】（1）利用等差数列的性质及得到，解方程即可；
（2）利用公式法、错位相减法分别求出，再作差比较即可.
【详解】（1）因为是首项为1的等比数列且，，成等差数列，
所以，所以，
即，解得，所以，
所以.
（2）[方法一]：作差后利用错位相减法求和
，
，
．
设， ⑧
则． ⑨
由⑧-⑨得．
所以．
因此．
故．
[方法二]【最优解】：公式法和错位相减求和法
证明：由（1）可得，
，①
，②
①②得 ，
所以，
所以，
所以.
[方法三]：构造裂项法
由（Ⅰ）知，令，且，即，
通过等式左右两边系数比对易得，所以．
则，下同方法二．
[方法四]：导函数法
设，
由于，
则．
又，
所以
，下同方法二．
【整体点评】本题主要考查数列的求和，涉及到等差数列的性质，错位相减法求数列的和，考查学生的数学运算能力，是一道中档题，其中证明不等式时采用作差法，或者作商法要根据式子得结构类型灵活选择，关键是要看如何消项化简的更为简洁.
（2）的方法一直接作差后利用错位相减法求其部分和，进而证得结论；
方法二根据数列的不同特点，分别利用公式法和错位相减法求得,然后证得结论,为最优解；
方法三采用构造数列裂项求和的方法，关键是构造，使，求得的表达式，这是错位相减法的一种替代方法，
方法四利用导数方法求和，也是代替错位相减求和法的一种方法.
22．证明过程见解析
【分析】选①②作条件证明③时，可设出，结合的关系求出，利用是等差数列可证；也可分别设出公差，写出各自的通项公式后利用两者的关系，对照系数，得到等量关系，进行证明.
选①③作条件证明②时，根据等差数列的求和公式表示出，结合等差数列定义可证；
选②③作条件证明①时，设出，结合的关系求出，根据可求，然后可证是等差数列；也可利用前两项的差求出公差，然后求出通项公式，进而证明出结论.
【详解】选①②作条件证明③：
[方法一]：待定系数法+与关系式
设，则，
当时，；
当时，；
因为也是等差数列，所以，解得；
所以，，故.
[方法二] ：待定系数法
设等差数列的公差为d，等差数列的公差为，
则，将代入，
化简得对于恒成立．
则有，解得．所以．
选①③作条件证明②：
因为，是等差数列，
所以公差，
所以，即，
因为，
所以是等差数列.
选②③作条件证明①：
[方法一]：定义法
设，则，
当时，；
当时，；
因为，所以，解得或；
当时，，当时，满足等差数列的定义，此时为等差数列；
当时，，不合题意，舍去.
综上可知为等差数列.
[方法二]【最优解】：求解通项公式
因为，所以，，因为也为等差数列，所以公差，所以，故，当时，，当时，满足上式，故的通项公式为，所以，，符合题意.
【整体点评】这类题型在解答题中较为罕见，求解的关键是牢牢抓住已知条件，结合相关公式，逐步推演，选①②时，法一：利用等差数列的通项公式是关于的一次函数，直接设出，平方后得到的关系式，利用得到的通项公式，进而得到，是选择①②证明③的通式通法；法二：分别设出与的公差，写出各自的通项公式后利用两者的关系，对照系数，得到等量关系，，进而得到；选①③时，按照正常的思维求出公差，表示出及，进而由等差数列定义进行证明；选②③时，法一：利用等差数列的通项公式是关于的一次函数，直接设出，结合的关系求出，根据可求，然后可证是等差数列；法二：利用是等差数列即前两项的差求出公差，然后求出的通项公式，利用，求出的通项公式，进而证明出结论.
23．（1）；（2）.
【分析】(1)方法一：由题意结合递推关系式确定数列的特征，然后求和其通项公式即可；
(2)方法二：分组求和，结合等差数列前项和公式即可求得数列的前20项和.
【详解】解：（1）[方法一]【最优解】：
显然为偶数，则，
所以，即，且，
所以是以2为首项，3为公差的等差数列，
于是．
[方法二]：奇偶分类讨论
由题意知，所以．
由（为奇数）及（为偶数）可知，
数列从第一项起，
若为奇数，则其后一项减去该项的差为1，
若为偶数，则其后一项减去该项的差为2．
所以，则．
[方法三]：累加法
由题意知数列满足．
所以，
，
则．
所以，数列的通项公式．
（2）[方法一]：奇偶分类讨论
．
[方法二]：分组求和
由题意知数列满足，
所以．
所以数列的奇数项是以1为首项，3为公差的等差数列；
同理，由知数列的偶数项是以2为首项，3为公差的等差数列．
从而数列的前20项和为：
．
【整体点评】(1)方法一：由题意讨论的性质为最一般的思路和最优的解法；
方法二：利用递推关系式分类讨论奇偶两种情况，然后利用递推关系式确定数列的性质；
方法三：写出数列的通项公式，然后累加求数列的通项公式，是一种更加灵活的思路.
(2)方法一：由通项公式分奇偶的情况求解前项和是一种常规的方法；
方法二：分组求和是常见的数列求和的一种方法，结合等差数列前项和公式和分组的方法进行求和是一种不错的选择.
24．证明见解析.
【分析】先根据求出数列的公差，进一步写出的通项，从而求出的通项公式，最终得证.
【详解】∵数列是等差数列，设公差为
∴，
∴，
∴当时，
当时，，满足，
∴的通项公式为，
∴
∴是等差数列.
【点睛】在利用求通项公式时一定要讨论的特殊情况.
25．（I），；（II）（i）证明见解析；（ii）证明见解析.
【分析】（I）由等差数列的求和公式运算可得的通项，由等比数列的通项公式运算可得的通项公式；
（II）（i）运算可得，结合等比数列的定义即可得证；
（ii）放缩得，进而可得，结合错位相减法即可得证.
【详解】（I）因为是公差为2的等差数列，其前8项和为64．
所以，所以，
所以；
设等比数列的公比为，
所以，解得（负值舍去），
所以；
（II）（i）由题意，，
所以，
所以，且，
所以数列是等比数列；
（ii）由题意知，，
所以，
所以，
设，
则，
两式相减得，
所以，
所以.
【点睛】关键点点睛：
最后一问考查数列不等式的证明，因为无法直接求解，应先放缩去除根号，再由错位相减法即可得证.
26．（Ⅰ），；（Ⅱ）证明见解析；（Ⅲ）.
【分析】(Ⅰ)由题意分别求得数列的公差、公比，然后利用等差、等比数列的通项公式得到结果；
(Ⅱ)利用(Ⅰ)的结论首先求得数列前n项和，然后利用作差法证明即可；
(Ⅲ)分类讨论n为奇数和偶数时数列的通项公式，然后分别利用指数型裂项求和和错位相减求和计算和的值，据此进一步计算数列的前2n项和即可.
【详解】(Ⅰ)设等差数列的公差为，等比数列的公比为q.
由，，可得d=1.
从而的通项公式为.
由，
又q≠0，可得，解得q=2，
从而的通项公式为.
(Ⅱ)证明：由(Ⅰ)可得，
故，，
从而，
所以.
(Ⅲ)当n为奇数时，，
当n为偶数时，，
对任意的正整数n，有，
和 ①
由①得 ②
由①②得，
由于，
从而得：.
因此，.
所以，数列的前2n项和为.
【点睛】本题主要考查数列通项公式的求解，分组求和法，指数型裂项求和，错位相减求和等，属于中等题.
27．140里.
【分析】由条件确定，该男子这9天中每天走的路程数构成等差数列，根据等差数列的通项公式，和前项和公式，列式求解.
【详解】解：因为从第2天起，每天比前一天多走的路程相同，
所以该男子这9天中每天走的路程数构成等差数列，
设该数列为，第1天走的路程数为首项，公差为，
则，.
因为，，
所以，解得，
则，
所以该男子第5天走140里.
28．（1）；（2），最小值为–16．
【分析】（1）方法一：根据等差数列前n项和公式，求出公差，再代入等差数列通项公式即得结果；
（2）方法二：根据等差数列前n项和公式得，根据二次函数的性质即可求出.
【详解】（1）[方法一]：【通性通法】【最优解】 公式法
设等差数列的公差为，由得，，解得：，所以．
[方法二]：函数+待定系数法
设等差数列通项公式为，易得，由，即，即，解得：，所以．
（2）[方法1]：邻项变号法
由可得．当，即，解得，所以的最小值为，
所以的最小值为．
[方法2]：函数法
由题意知，即，
所以的最小值为，所以的最小值为．
【整体点评】（1）方法一：直接根据基本量的计算，利用等差数列前n项和公式求出公差，即可得到通项公式，是该题的通性通法，也是最优解；
方法二：根据等差数列的通项公式的函数形式特征，以及等差数列前n项和的性质，用待定系数法解方程组求解；
（2）方法一：利用等差数列前n项和公式求，再利用邻项变号法求最值；
方法二：利用等差数列前n项和公式求，再根据二次函数性质求最值．
29．（1）见解析；（2），．
【分析】(1)可通过题意中的以及对两式进行相加和相减即可推导出数列是等比数列以及数列是等差数列；
(2)可通过(1)中的结果推导出数列以及数列的通项公式，然后利用数列以及数列的通项公式即可得出结果．
【详解】(1)由题意可知，，，，
所以，即，
所以数列是首项为、公比为的等比数列，，
因为，
所以，数列是首项、公差为的等差数列，．
(2)由(1)可知，，，
所以，．
【点睛】本题考查了数列的相关性质，主要考查了等差数列以及等比数列的相关证明，证明数列是等差数列或者等比数列一定要结合等差数列或者等比数列的定义，考查推理能力，考查化归与转化思想，是中档题．
30．（1）；
（2）.
【分析】（1）首项设出等差数列的首项和公差，根据题的条件，建立关于和的方程组，求得和的值，利用等差数列的通项公式求得结果；
（2）根据题意有，根据，可知，根据，得到关于的不等式，从而求得结果.
【详解】（1）设等差数列的首项为，公差为，
根据题意有，
解答，所以，
所以等差数列的通项公式为；
（2）由条件，得，即，
因为，所以，并且有，所以有，
由得，整理得，
因为，所以有，即，
解得，
所以的取值范围是：
【点睛】该题考查的是有关数列的问题，涉及到的知识点有等差数列的通项公式，等差数列的求和公式，在解题的过程中，需要认真分析题意，熟练掌握基础知识是正确解题的关键.
31．（1）；（2）.
【分析】(1)本题首先可以根据数列是等比数列将转化为，转化为，再然后将其带入中，并根据数列是各项均为正数以及即可通过运算得出结果；
(2)本题可以通过数列的通项公式以及对数的相关性质计算出数列的通项公式，再通过数列的通项公式得知数列是等差数列，最后通过等差数列求和公式即可得出结果．
【详解】(1)因为数列是各项均为正数的等比数列，，，
所以令数列的公比为，，，
所以，解得(舍去)或，
所以数列是首项为、公比为的等比数列，．
(2)因为，所以，，，
所以数列是首项为、公差为的等差数列，．
【点睛】本题考查数列的相关性质，主要考查等差数列以及等比数列的通项公式的求法，考查等差数列求和公式的使用，考查化归与转化思想，考查计算能力，是简单题．