4-指数函数、对数函数、幂函数-五年（2018-2022）高考数学真题按知识点分类汇编

这是一份4-指数函数、对数函数、幂函数-五年（2018-2022）高考数学真题按知识点分类汇编，共23页。试卷主要包含了单选题，多选题，填空题，双空题等内容，欢迎下载使用。

一、单选题
1．（2022·天津·统考高考真题）化简的值为（ ）
A．1B．2C．4D．6
2．（2022·天津·统考高考真题）已知，，，则（ ）
A．B．C．D．
3．（2022·浙江·统考高考真题）已知，则（ ）
A．25B．5C．D．
4．（2022·全国·统考高考真题）已知，则（ ）
A．B．C．D．
5．（2022·北京·统考高考真题）已知函数，则对任意实数x，有（ ）
A．B．
C．D．
6．（2022·北京·统考高考真题）在北京冬奥会上，国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术，为实现绿色冬奥作出了贡献．如图描述了一定条件下二氧化碳所处的状态与T和的关系，其中T表示温度，单位是K；P表示压强，单位是．下列结论中正确的是（ ）
A．当，时，二氧化碳处于液态
B．当，时，二氧化碳处于气态
C．当，时，二氧化碳处于超临界状态
D．当，时，二氧化碳处于超临界状态
7．（2022·全国·统考高考真题）设，则（ ）
A．B．C．D．
8．（2021·天津·统考高考真题）设，则a，b，c的大小关系为（ ）
A．B．C．D．
9．（2021·天津·统考高考真题）若，则（ ）
A．B．C．1D．
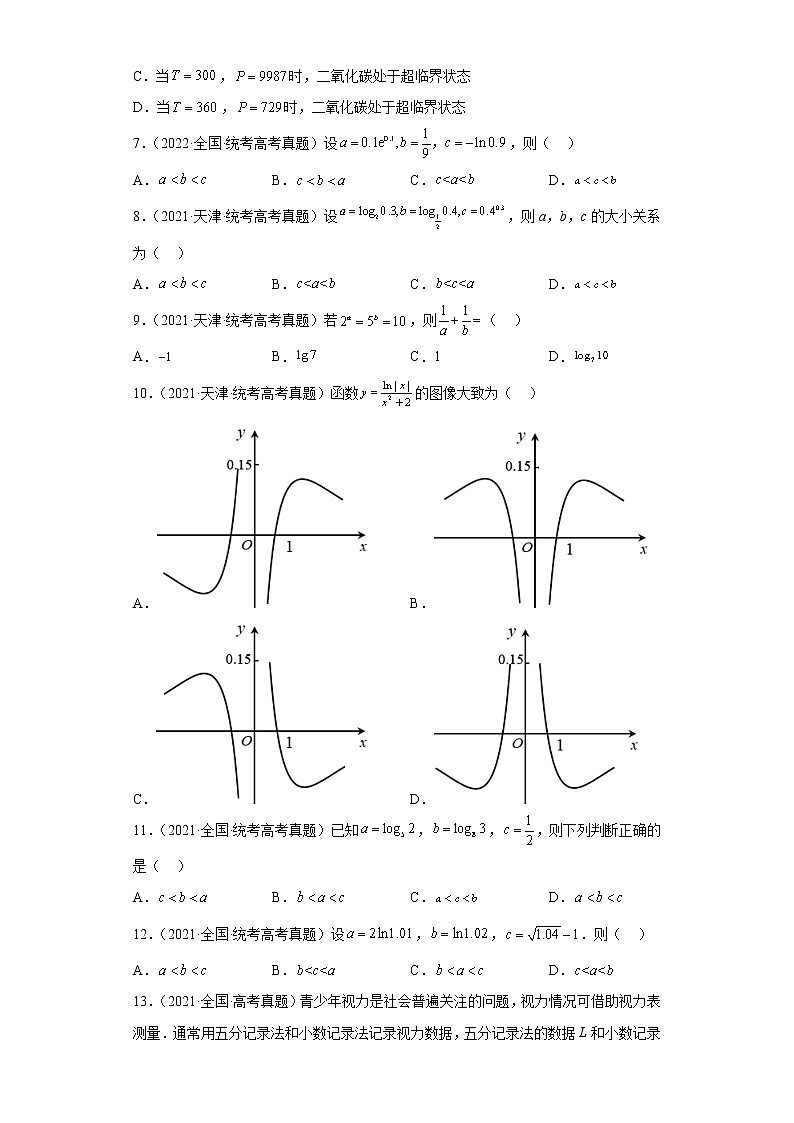
10．（2021·天津·统考高考真题）函数的图像大致为（ ）
A．B．
C．D．
11．（2021·全国·统考高考真题）已知，，，则下列判断正确的是（ ）
A．B．C．D．
12．（2021·全国·统考高考真题）设，，．则（ ）
A．B．C．D．
13．（2021·全国·高考真题）青少年视力是社会普遍关注的问题，视力情况可借助视力表测量．通常用五分记录法和小数记录法记录视力数据，五分记录法的数据L和小数记录表的数据V的满足．已知某同学视力的五分记录法的数据为4.9，则其视力的小数记录法的数据为（ ）（）
A．1.5B．1.2C．0.8D．0.6
14．（2021·全国·统考高考真题）下列函数中最小值为4的是（ ）
A．B．
C．D．
15．（2020·山东·统考高考真题）函数的定义域是（ ）
A．B．C．D．
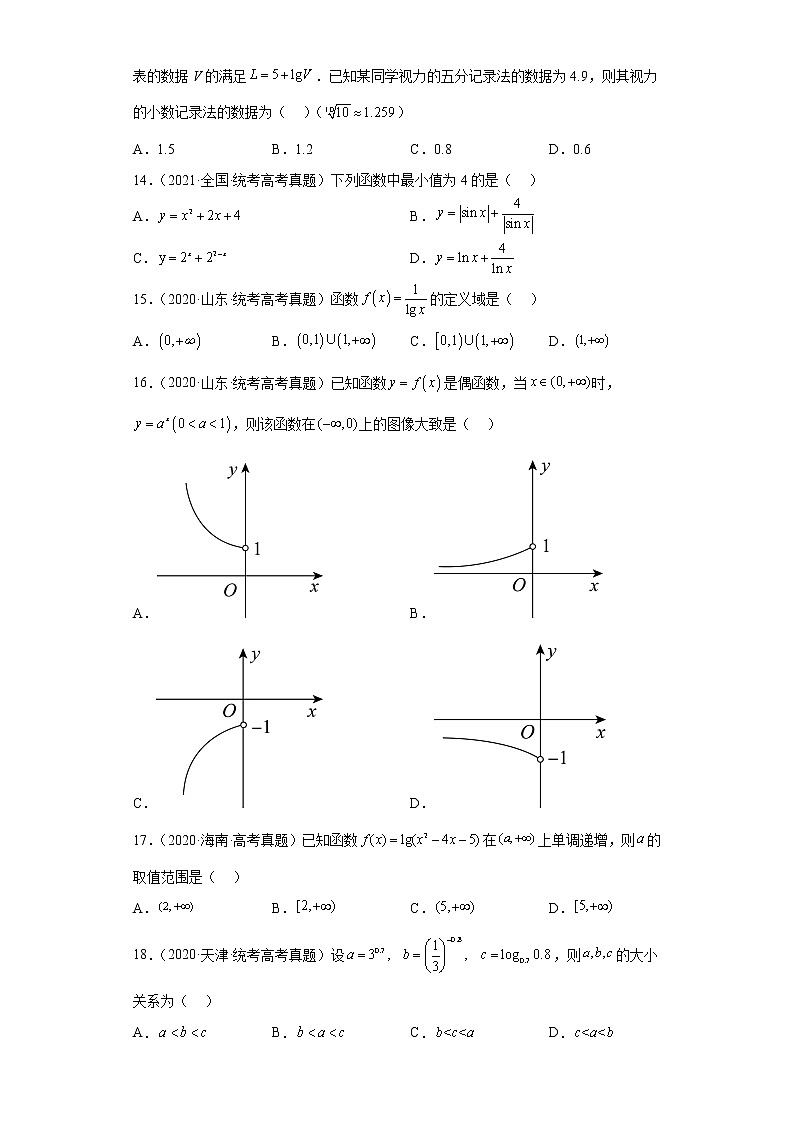
16．（2020·山东·统考高考真题）已知函数是偶函数，当时，，则该函数在上的图像大致是（ ）
A．B．
C．D．
17．（2020·海南·高考真题）已知函数在上单调递增，则的取值范围是（ ）
A．B．C．D．
18．（2020·天津·统考高考真题）设，则的大小关系为（ ）
A．B．C．D．
19．（2020·全国·统考高考真题）若，则（ ）
A．B．C．D．
20．（2020·全国·统考高考真题）已知55<84，134<85．设a=lg53，b=lg85，c=lg138，则（ ）
A．a21．（2020·全国·统考高考真题）Lgistic模型是常用数学模型之一，可应用于流行病学领域．有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I(t)(t的单位：天)的Lgistic模型：，其中K为最大确诊病例数．当I()=0.95K时，标志着已初步遏制疫情，则约为（ ）（ln19≈3）
A．60B．63C．66D．69
22．（2020·全国·统考高考真题）设，，，则（ ）
A．B．C．D．
23．（2020·全国·统考高考真题）设，则（ ）
A．B．C．D．
24．（2020·全国·统考高考真题）设函数，则f(x)（ ）
A．是偶函数，且在单调递增B．是奇函数，且在单调递减
C．是偶函数，且在单调递增D．是奇函数，且在单调递减
25．（2019·全国·高考真题）已知，则
A．B．C．D．
26．（2019·全国·高考真题）若a>b，则
A．ln(a−b)>0B．3a<3b
C．a3−b3>0D．│a│>│b│
27．（2019·北京·高考真题）在天文学中，天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足，其中星等为mk的星的亮度为Ek（k=1,2）.已知太阳的星等是–26.7，天狼星的星等是–1.45，则太阳与天狼星的亮度的比值为
A．1010.1B．10.1C．lg10.1D．
28．（2019·天津·高考真题）已知，，，则的大小关系为
A．B．
C．D．
29．（2019·天津·高考真题）已知，，，则的大小关系为
A．B．
C．D．
30．（2018·天津·高考真题）已知，，，则a，b，c的大小关系为
A．B．C．D．
31．（2018·全国·高考真题）设，，则
A．B．
C．D．
32．（2018·全国·高考真题）下列函数中，其图像与函数的图像关于直线对称的是
A．B．C．D．
33．（2018·天津·高考真题）已知，则的大小关系为
A．B．C．D．
二、多选题
34．（2020·海南·统考高考真题）信息熵是信息论中的一个重要概念.设随机变量X所有可能的取值为，且，定义X的信息熵.（ ）
A．若n=1，则H(X)=0
B．若n=2，则H(X)随着的增大而增大
C．若，则H(X)随着n的增大而增大
D．若n=2m，随机变量Y所有可能的取值为，且，则H(X)≤H(Y)
三、填空题
35．（2020·山东·统考高考真题）若，则实数的值是______.
36．（2020·北京·统考高考真题）函数的定义域是____________．
37．（2020·江苏·统考高考真题）已知y=f(x)是奇函数，当x≥0时， ，则f(-8)的值是____.
38．（2018·全国·高考真题）已知函数，若，则________．
四、双空题
39．（2022·全国·统考高考真题）若是奇函数，则_____，______．
参考答案：
1．B
【分析】根据对数的性质可求代数式的值.
【详解】原式
，
故选：B
2．C
【分析】利用幂函数、对数函数的单调性结合中间值法可得出、、的大小关系.
【详解】因为，故.
故答案为：C.
3．C
【分析】根据指数式与对数式的互化，幂的运算性质以及对数的运算性质即可解出．
【详解】因为，，即，所以．
故选：C.
4．A
【分析】法一：根据指对互化以及对数函数的单调性即可知，再利用基本不等式，换底公式可得，，然后由指数函数的单调性即可解出．
【详解】［方法一］：（指对数函数性质）
由可得，而，所以，即，所以.
又，所以，即，
所以.综上，.
［方法二］：【最优解】（构造函数）
由，可得．
根据的形式构造函数 ，则，
令，解得 ，由 知 .
在 上单调递增，所以 ，即 ，
又因为 ，所以 .
故选：A.
【整体点评】法一：通过基本不等式和换底公式以及对数函数的单调性比较，方法直接常用，属于通性通法；
法二：利用的形式构造函数，根据函数的单调性得出大小关系，简单明了，是该题的最优解．
5．C
【分析】直接代入计算，注意通分不要计算错误．
【详解】，故A错误，C正确；
，不是常数，故BD错误；
故选：C．
6．D
【分析】根据与的关系图可得正确的选项.
【详解】当，时，，此时二氧化碳处于固态，故A错误.
当，时，，此时二氧化碳处于液态，故B错误.
当，时，与4非常接近，故此时二氧化碳处于固态，对应的是非超临界状态，故C错误.
当，时，因, 故此时二氧化碳处于超临界状态，故D正确.
故选：D
7．C
【分析】构造函数， 导数判断其单调性，由此确定的大小.
【详解】方法一：构造法
设，因为，
当时，，当时，
所以函数在单调递减，在上单调递增，
所以，所以，故，即，
所以，所以，故，所以，
故，
设，则,
令，，
当时，，函数单调递减，
当时，，函数单调递增，
又，
所以当时，，
所以当时，，函数单调递增，
所以，即，所以
故选：C.
方法二：比较法
解： ， ， ，
① ，
令
则 ，
故 在 上单调递减，
可得 ，即 ，所以 ；
② ，
令
则 ，
令 ，所以 ，
所以 在 上单调递增，可得 ，即 ，
所以 在 上单调递增，可得 ，即 ，所以
故
8．D
【分析】根据指数函数和对数函数的性质求出的范围即可求解.
【详解】，，
，，
，，
.
故选：D.
9．C
【分析】由已知表示出，再由换底公式可求.
【详解】，，
.
故选：C.
10．B
【分析】由函数为偶函数可排除AC，再由当时，，排除D，即可得解.
【详解】设，则函数的定义域为，关于原点对称，
又，所以函数为偶函数，排除AC；
当时， ，所以，排除D.
故选：B.
11．C
【分析】对数函数的单调性可比较、与的大小关系，由此可得出结论.
【详解】，即.
故选：C.
12．B
【分析】利用对数的运算和对数函数的单调性不难对a,b的大小作出判定，对于a与c，b与c的大小关系，将0.01换成x,分别构造函数,，利用导数分析其在0的右侧包括0.01的较小范围内的单调性，结合f(0)=0,g(0)=0即可得出a与c，b与c的大小关系.
【详解】[方法一]：
，
所以；
下面比较与的大小关系.
记，则，，
由于
所以当0所以在上单调递增，
所以，即，即；
令，则，，
由于，在x>0时，，
所以，即函数在[0，+∞)上单调递减，所以，即，即b综上，，
故选：B.
[方法二]：
令
，即函数在（1，+∞)上单调递减
令
，即函数在（1，3)上单调递增
综上，，
故选：B.
【点睛】本题考查比较大小问题，难度较大，关键难点是将各个值中的共同的量用变量替换，构造函数，利用导数研究相应函数的单调性，进而比较大小，这样的问题，凭借近似估计计算往往是无法解决的.
13．C
【分析】根据关系，当时，求出，再用指数表示，即可求解.
【详解】由，当时，，
则.
故选：C.
14．C
【分析】根据二次函数的性质可判断选项不符合题意，再根据基本不等式“一正二定三相等”，即可得出不符合题意，符合题意．
【详解】对于A，，当且仅当时取等号，所以其最小值为，A不符合题意；
对于B，因为，，当且仅当时取等号，等号取不到，所以其最小值不为，B不符合题意；
对于C，因为函数定义域为，而，，当且仅当，即时取等号，所以其最小值为，C符合题意；
对于D，，函数定义域为，而且，如当，，D不符合题意．
故选：C．
【点睛】本题解题关键是理解基本不等式的使用条件，明确“一正二定三相等”的意义，再结合有关函数的性质即可解出．
15．B
【分析】根据题意得到，再解不等式组即可.
【详解】由题知：，解得且.
所以函数定义域为.
故选：B
16．B
【分析】根据偶函数，指数函数的知识确定正确选项.
【详解】当时，，所以在上递减，
是偶函数，所以在上递增.
注意到，
所以B选项符合.
故选：B
17．D
【分析】首先求出的定义域，然后求出的单调递增区间即可.
【详解】由得或
所以的定义域为
因为在上单调递增
所以在上单调递增
所以
故选：D
【点睛】在求函数的单调区间时一定要先求函数的定义域.
18．D
【分析】利用指数函数与对数函数的性质，即可得出的大小关系.
【详解】因为，
，
，
所以.
故选：D.
【点睛】本题考查的是有关指数幂和对数值的比较大小问题，在解题的过程中，注意应用指数函数和对数函数的单调性，确定其对应值的范围.
比较指对幂形式的数的大小关系，常用方法：
（1）利用指数函数的单调性：，当时，函数递增；当时，函数递减；
（2）利用对数函数的单调性：，当时，函数递增；当时，函数递减；
（3）借助于中间值，例如：0或1等.
19．A
【分析】将不等式变为，根据的单调性知，以此去判断各个选项中真数与的大小关系，进而得到结果.
【详解】由得：，
令，
为上的增函数，为上的减函数，为上的增函数，
，
，，，则A正确，B错误；
与的大小不确定，故CD无法确定.
故选：A.
【点睛】本题考查对数式的大小的判断问题，解题关键是能够通过构造函数的方式，利用函数的单调性得到的大小关系，考查了转化与化归的数学思想.
20．A
【分析】由题意可得、、，利用作商法以及基本不等式可得出、的大小关系，由，得，结合可得出，由，得，结合，可得出，综合可得出、、的大小关系.
【详解】由题意可知、、，，；
由，得，由，得，，可得；
由，得，由，得，，可得.
综上所述，.
故选：A.
【点睛】本题考查对数式的大小比较，涉及基本不等式、对数式与指数式的互化以及指数函数单调性的应用，考查推理能力，属于中等题.
21．C
【分析】将代入函数结合求得即可得解.
【详解】，所以，则，
所以，，解得.
故选：C.
【点睛】本题考查对数的运算，考查指数与对数的互化，考查计算能力，属于中等题.
22．A
【分析】分别将,改写为，，再利用单调性比较即可.
【详解】因为，，
所以.
故选：A.
【点晴】本题考查对数式大小的比较，考查学生转化与化归的思想，是一道中档题.
23．B
【分析】根据已知等式，利用指数对数运算性质即可得解
【详解】由可得，所以，
所以有，
故选：B.
【点睛】本题考查的是有关指对式的运算的问题，涉及到的知识点有对数的运算法则，指数的运算法则，属于基础题目.
24．D
【分析】根据奇偶性的定义可判断出为奇函数，排除AC；当时，利用函数单调性的性质可判断出单调递增，排除B；当时，利用复合函数单调性可判断出单调递减，从而得到结果.
【详解】由得定义域为，关于坐标原点对称，
又，
为定义域上的奇函数，可排除AC；
当时，，
在上单调递增，在上单调递减，
在上单调递增，排除B；
当时，，
在上单调递减，在定义域内单调递增，
根据复合函数单调性可知：在上单调递减，D正确.
故选：D.
【点睛】本题考查函数奇偶性和单调性的判断；判断奇偶性的方法是在定义域关于原点对称的前提下，根据与的关系得到结论；判断单调性的关键是能够根据自变量的范围化简函数，根据单调性的性质和复合函数“同增异减”性得到结论.
25．B
【分析】运用中间量比较，运用中间量比较
【详解】则．故选B．
【点睛】本题考查指数和对数大小的比较，渗透了直观想象和数学运算素养．采取中间变量法，利用转化与化归思想解题．
26．C
【分析】本题也可用直接法，因为，所以，当时，，知A错，因为是增函数，所以，故B错；因为幂函数是增函数，，所以，知C正确；取，满足，，知D错．
【详解】取，满足，，知A错，排除A；因为，知B错，排除B；取，满足，，知D错，排除D，因为幂函数是增函数，，所以，故选C．
【点睛】本题主要考查对数函数性质、指数函数性质、幂函数性质及绝对值意义，渗透了逻辑推理和运算能力素养，利用特殊值排除即可判断．
27．A
【解析】由题意得到关于的等式，结合对数的运算法则可得亮度的比值.
【详解】两颗星的星等与亮度满足,令,
.
故选A.
【点睛】本题以天文学问题为背景,考查考生的数学应用意识､信息处理能力､阅读理解能力以及指数对数运算.
28．A
【分析】利用利用等中间值区分各个数值的大小．
【详解】；
；
．
故．
故选A．
【点睛】利用指数函数、对数函数的单调性时要根据底数与的大小区别对待．
29．A
【解析】利用等中间值区分各个数值的大小．
【详解】，
，
，故，
所以．
故选A．
【点睛】本题考查大小比较问题，关键选择中间量和函数的单调性进行比较．
30．D
【详解】分析：由题意结合对数函数的性质整理计算即可求得最终结果.
详解：由题意结合对数函数的性质可知：
，，，
据此可得：.
本题选择D选项.
点睛：对于指数幂的大小的比较，我们通常都是运用指数函数的单调性，但很多时候，因幂的底数或指数不相同，不能直接利用函数的单调性进行比较．这就必须掌握一些特殊方法．在进行指数幂的大小比较时，若底数不同，则首先考虑将其转化成同底数，然后再根据指数函数的单调性进行判断．对于不同底而同指数的指数幂的大小的比较，利用图象法求解，既快捷，又准确．
31．B
【详解】分析：求出，得到的范围，进而可得结果．
详解：.
,即
又
即
故选B.
点睛：本题主要考查对数的运算和不等式，属于中档题．
32．B
【详解】分析：确定函数过定点（1，0）关于x=1对称点，代入选项验证即可．
详解：函数过定点（1，0），（1，0）关于x=1对称的点还是（1，0），只有过此点．
故选项B正确
点睛：本题主要考查函数的对称性和函数的图像，属于中档题．
33．D
【详解】分析：由题意结合对数的性质，对数函数的单调性和指数的性质整理计算即可确定a,b,c的大小关系.
详解：由题意可知：，即，，即，
，即，综上可得：.本题选择D选项.
点睛：对于指数幂的大小的比较，我们通常都是运用指数函数的单调性，但很多时候，因幂的底数或指数不相同，不能直接利用函数的单调性进行比较．这就必须掌握一些特殊方法．在进行指数幂的大小比较时，若底数不同，则首先考虑将其转化成同底数，然后再根据指数函数的单调性进行判断．对于不同底而同指数的指数幂的大小的比较，利用图象法求解，既快捷，又准确．
34．AC
【分析】对于A选项，求得，由此判断出A选项；对于B选项，利用特殊值法进行排除；对于C选项，计算出，利用对数函数的性质可判断出C选项；对于D选项，计算出 ，利用基本不等式和对数函数的性质判断出D选项.
【详解】对于A选项，若，则，所以，所以A选项正确.
对于B选项，若，则，，
所以，
当时，，
当时，，
两者相等，所以B选项错误.
对于C选项，若，则
，
则随着的增大而增大，所以C选项正确.
对于D选项，若，随机变量的所有可能的取值为，且 （ ）.
.
由于，所以 ，所以 ，
所以，
所以，所以D选项错误.
故选：AC
【点睛】本小题主要考查对新定义“信息熵”的理解和运用，考查分析、思考和解决问题的能力，涉及对数运算和对数函数及不等式的基本性质的运用，属于难题.
35．
【分析】根据对数运算化简为，求解的值.
【详解】，
即，解得：.
故答案为：
36．
【分析】根据分母不为零、真数大于零列不等式组，解得结果.
【详解】由题意得，
故答案为：
【点睛】本题考查函数定义域，考查基本分析求解能力，属基础题.
37．
【分析】先求，再根据奇函数求
【详解】，因为为奇函数，所以
故答案为：
【点睛】本题考查根据奇函数性质求函数值，考查基本分析求解能力，属基础题.
38．-7
【详解】分析：首先利用题的条件，将其代入解析式，得到，从而得到，从而求得，得到答案.
详解：根据题意有，可得，所以，故答案是.
点睛：该题考查的是有关已知某个自变量对应函数值的大小，来确定有关参数值的问题，在求解的过程中，需要将自变量代入函数解析式，求解即可得结果，属于基础题目.
39． ； ．
【分析】根据奇函数的定义即可求出．
【详解】[方法一]：奇函数定义域的对称性
若，则的定义域为，不关于原点对称
若奇函数的有意义，则且
且，
函数为奇函数，定义域关于原点对称，
，解得，
由得，，
，
故答案为：；．
[方法二]：函数的奇偶性求参
函数为奇函数
[方法三]：
因为函数为奇函数，所以其定义域关于原点对称．
由可得，，所以，解得：，即函数的定义域为，再由可得，．即，在定义域内满足，符合题意．
故答案为：；．