高中数学高考专题04 立体几何（原卷版）

这是一份高中数学高考专题04 立体几何（原卷版），共13页。
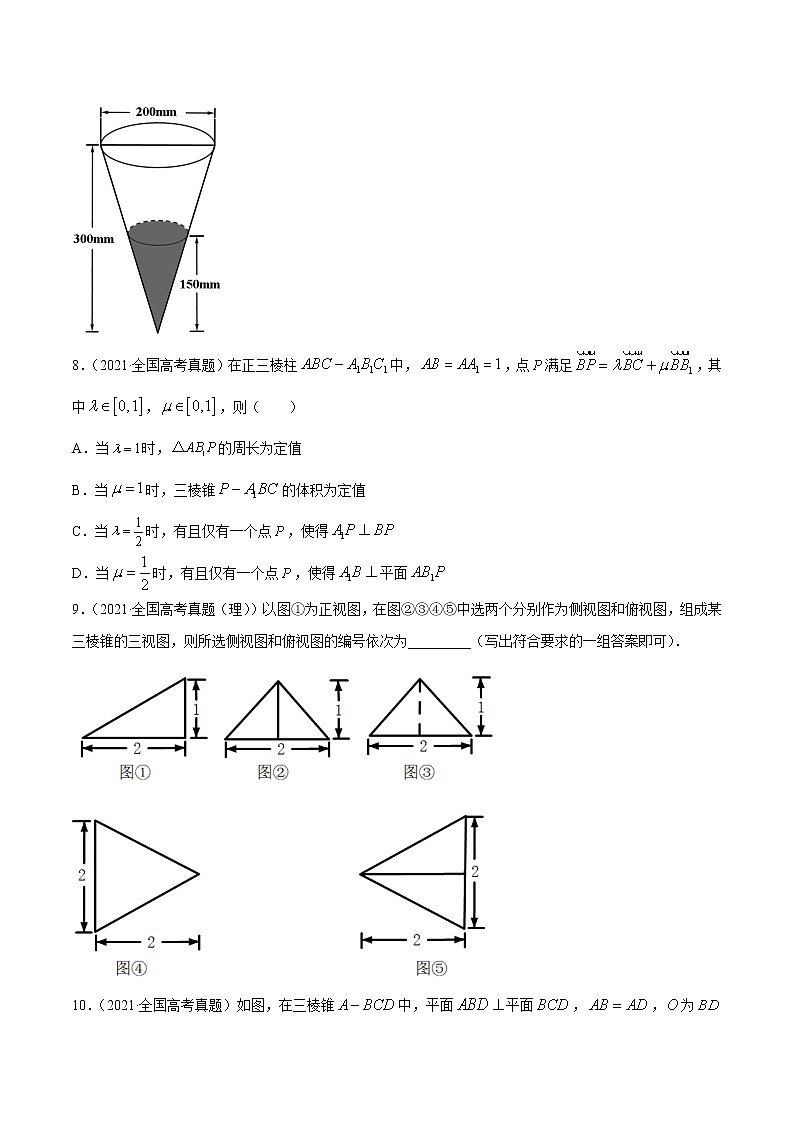
专题04 立体几何1．（2021·浙江高考真题）某几何体的三视图如图所示，则该几何体的体积是（    ）A． B．3 C． D．2．（2021·北京高考真题）某四面体的三视图如图所示，该四面体的表面积为（    ）A． B．4 C． D．23．（2021·浙江高考真题）如图已知正方体，M，N分别是，的中点，则（    ）A．直线与直线垂直，直线平面B．直线与直线平行，直线平面C．直线与直线相交，直线平面D．直线与直线异面，直线平面4．（2021·全国高考真题（理））已如A，B，C是半径为1的球O的球面上的三个点，且，则三棱锥的体积为（    ）A． B． C． D．5．（2021·全国高考真题（理））在正方体中，P为的中点，则直线与所成的角为（    ）A． B． C． D．6．（2021·全国高考真题）已知圆锥的底面半径为，其侧面展开图为一个半圆，则该圆锥的母线长为（    ）A． B． C． D．7．（2021·北京高考真题）定义：24小时内降水在平地上积水厚度（）来判断降雨程度．其中小雨（），中雨（），大雨（），暴雨（），小明用一个圆锥形容器接了24小时的雨水，如图，则这天降雨属于哪个等级（    ）8．（2021·全国高考真题）在正三棱柱中，，点满足，其中，，则（    ）A．当时，的周长为定值B．当时，三棱锥的体积为定值C．当时，有且仅有一个点，使得D．当时，有且仅有一个点，使得平面9．（2021·全国高考真题（理））以图①为正视图，在图②③④⑤中选两个分别作为侧视图和俯视图，组成某三棱锥的三视图，则所选侧视图和俯视图的编号依次为_________（写出符合要求的一组答案即可）．10．（2021·全国高考真题）如图，在三棱锥中，平面平面，，为的中点.（1）证明：；（2）若是边长为1的等边三角形，点在棱上，，且二面角的大小为，求三棱锥的体积.11．（2021·浙江高考真题）如图，在四棱锥中，底面是平行四边形，，M，N分别为的中点，.（1）证明：；（2）求直线与平面所成角的正弦值.12．（2021·全国高考真题（理））已知直三棱柱中，侧面为正方形，，E，F分别为和的中点，D为棱上的点．（1）证明：；（2）当为何值时，面与面所成的二面角的正弦值最小?13．（2021·全国高考真题（理））如图，四棱锥的底面是矩形，底面，，为的中点，且．（1）求；（2）求二面角的正弦值．14．（2021·北京高考真题）已知正方体，点为中点，直线交平面于点．（1）证明：点为的中点；（2）若点为棱上一点，且二面角的余弦值为，求的值．1．（2021·河北饶阳中学高三其他模拟）如图，正方体的棱长为6，点F是棱的中点，AC与BD的交点为O，点M在棱BC上，且，动点T（不同于点M）在四边形ABCD内部及其边界上运动，且，则直线与TM所成角的余弦值为（    ）A． B． C． D．2．（2021·全国高三其他模拟（理））如图几何体为一个圆柱和圆锥的组合体，圆锥的底面和圆柱的一个底面重合，圆锥的顶点为，圆柱的上、下底面的圆心分别为，，若该几何体有半径为1的外接球，且球心为，则不正确的是（    ）A．如果圆锥的体积为圆柱体积的，则圆锥的体积为B．C．如果，则与重合．D．如果，则圆柱的体积为．3．（2021·全国高三其他模拟（理））若空间某几何体的三视图如图所示，则该几何体外接球的表面积是（    ）A． B． C． D．4．（2021·浙江杭州市·杭州高级中学高三其他模拟）某空间几何体的三视图如图所示，则该几何体的体积为（    ）A． B． C．8 D．165．（2021·浙江高三其他模拟）已知直线和平面，则下列结论一定成立的是（    ）A．若，则 B．若，，则C．若，，则 D．若，，则6．（2021·山西高三三模（理））已知四棱锥的五个顶点都在球的球面上，平面，底面是高为的等腰梯形，，，，则球的表面积为（    ）A． B． C． D．7．（2021·安徽华星学校高三其他模拟（文））已知四面体中，平面平面，是边长为的等边三角形，，，则四面体的体积为（    ）A． B． C． D．8．（2021·福建高三三模）如图，在直四棱柱中，，，，，点，，分别在棱，，上，若，，，四点共面，则下列结论错误的是（    ）A．任意点，都有B．任意点，四边形不可能为平行四边形C．存在点，使得为等腰直角三角形D．存在点，使得平面9．（2021·江苏高三其他模拟）如图，在中，，，，现将其放置在平面的上面，其中点，在平面的同一侧，点平面，与平面所成的角为，则点到平面的最大距离是（    ）A． B．20 C． D．3010．（2021·广东佛山市·高三其他模拟）已知梯形，，，，是线段上的动点；将沿着所在的直线翻折成四面体，翻折的过程中下列选项中正确的是（    ）A．不论何时，与都不可能垂直B．存在某个位置，使得平面C．直线与平面所成角存在最大值D．四面体的外接球的表面积的最小值为11．（2021·福建福州市·高三其他模拟）在正方体中，是棱的中点，是侧面内的动点，且与平面的垂线垂直，如图所示，下列说法正确的是（    ）A．点的轨迹是一条线段 B．与是异面直线C．与不可能平行 D．三棱锥的体积为定值12．（2021·山东济南市·高三其他模拟）正四棱柱ABCD﹣A1B1C1D1中，AB＝2，AA1＝4，E为AB的中点，点F满足，动点M在侧面AA1D1D内运动，且MB∥平面D1EF，则|MD|的取值范围是__________________．13．（2021·河南高三其他模拟（理））在三棱锥中，已知，，则直线与平面所成角的余弦值为___________.14．（2021·江苏南通市·高三其他模拟）如图，在正三棱锥中，是高上一点，，直线与底面所成角的正切值为.（1）求证：平面；（2）求三棱锥外接球的体积.15．（2021·河北饶阳中学高三其他模拟）在四棱锥中，底面是边长为2的菱形，，是等边三角形，O为的中点，E为的中点，.（1）求证：平面.（2）求平面与平面所成锐角的正切值.16．（2021·湖南高三其他模拟）在长方体中，已知，为的中点.（1）在线段上是否存在点，使得平面平面？若存在，请加以证明，若不存在，请说明理由；（2）设，，点在上且满足，求与平面所成角的余弦值.17．（2021·重庆高三其他模拟）已知正方体中，分别为棱的中点.（1）求证；四点共面；（2）求二面角的余弦值.18．（2021·山东高三其他模拟）在正六棱柱中，.（1）求到平面的距离；（2）求二面角的余弦值.19．（2021·上海市崇明中学高三其他模拟）如图，在四棱锥中，底面是直角梯形，，，点是的中点.（1）证明：直线平面；（2）者直线与平面所成角的正弦值为，求三棱锥的体积.20．（2021·河南高三其他模拟（理））如图，在四棱锥中，底面ABCD为边长为4的菱形，，，E为AB的中点，O为AD的中点，.（1）证明：.（2）求二面角的余弦值.