

高中数学高考第14讲 导数的概念及运算(教师版)
展开
这是一份高中数学高考第14讲 导数的概念及运算(教师版),共12页。试卷主要包含了导数的概念,基本初等函数的导数公式,复合函数的导数等内容,欢迎下载使用。
知识梳理
1.导数的概念
(1)函数y=f(x)在x=x0处的导数
一般地,称函数y=f(x)在x=x0处的瞬时变化率
eq^\(lim,\s\d4(Δx→0))eq \(lim,\s\d5(Δx→0))eq \f(f(x0+Δx)-f(x0),Δx)=eq \(lim,\s\d5(Δx→0))eq^\(lim,\s\d4(Δx→0))eq \f(Δy,Δx)为函数y=f(x)在x=x0处的导数,记作f′(x0)或y′|x=x0,即f′(x0)=eq \(lim,\s\d5(Δx→0))eq^\(lim,\s\d4(Δx→0))eq \f(Δy,Δx)=eq^\(lim,\s\d4(Δx→0))eq \(lim,\s\d5(Δx→0))eq \f(f(x0+Δx)-f(x0),Δx).
(2)导数的几何意义
函数f(x)在点x0处的导数f′(x0)的几何意义是在曲线y=f(x)上点P(x0,y0)处的切线的斜率(瞬时速度就是位移函数s(t)对时间t的导数).相应地,切线方程为y-y0=f′(x0)(x-x0).
(3)函数f(x)的导函数
称函数f′(x)=eq^\(lim,\s\d4(Δx→0))eq \(lim,\s\d5(Δx→0))eq \f(f(x+Δx)-f(x),Δx)为f(x)的导函数.
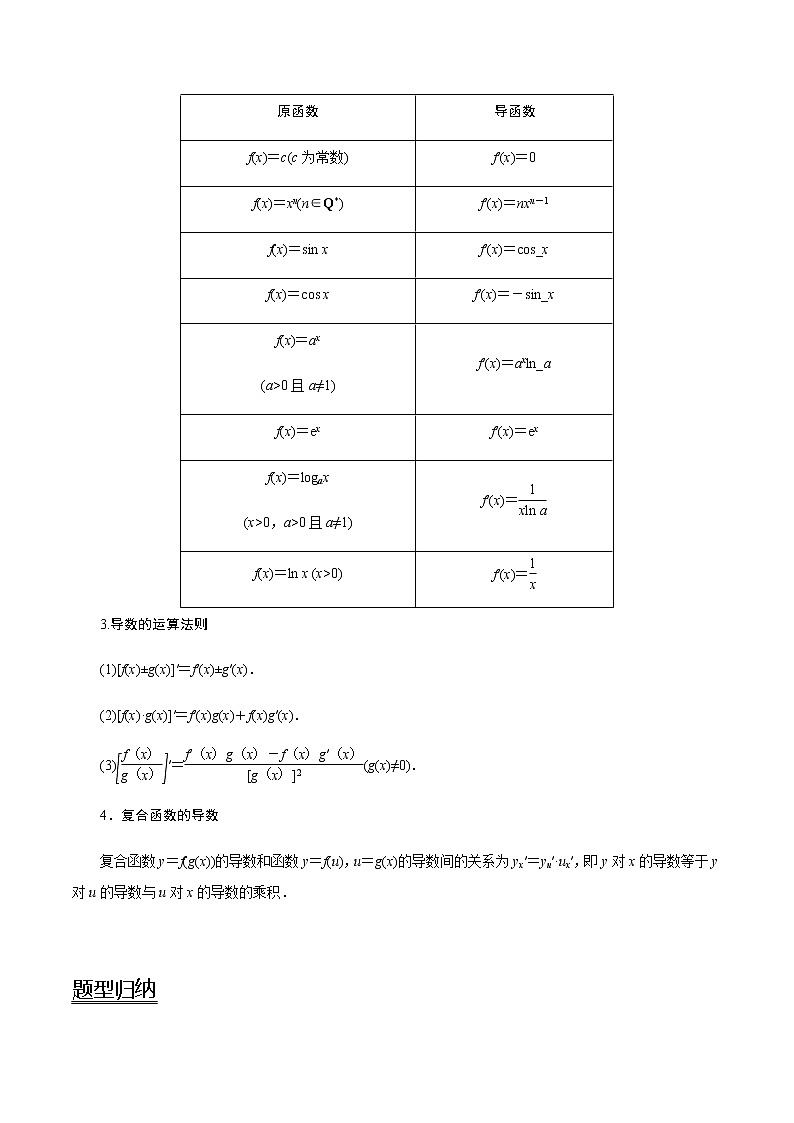
2.基本初等函数的导数公式
3.导数的运算法则
(1)[f(x)±g(x)]′=f′(x)±g′(x).
(2)[f(x)·g(x)]′=f′(x)g(x)+f(x)g′(x).
(3)eq \b\lc\[\rc\](\a\vs4\al\c1(\f(f(x),g(x))))′=eq \f(f′(x)g(x)-f(x)g′(x),[g(x)]2)(g(x)≠0).
4.复合函数的导数
复合函数y=f(g(x))的导数和函数y=f(u),u=g(x)的导数间的关系为yx′=yu′·ux′,即y对x的导数等于y对u的导数与u对x的导数的乘积.
题型归纳
题型1 导数的运算
【例1-1】(2020春•房山区期末)已知函数,则它的导函数等于
A.B. C.D.
【分析】根据题意,有导数的计算公式可得数(1),化简变形即可得答案.
【解答】解:根据题意,函数,其导数(1);
故选:.
【例1-2】(2020春•南阳期末)已知:函数,其导函数.若函数的导函数,且,则的值为
A.B.1C.D.
【分析】求出函数的解析式,计算的值即可.
【解答】解:由题意设,
则,符合题意,
故,解得:,
故,
,
故选:.
【跟踪训练1-1】(2020•新课标Ⅲ)设函数,若(1),则 .
【分析】先求出函数的导数,再根据(1),求得的值.
【解答】解:函数,,
若(1),,则,
故答案为:1.
【跟踪训练1-2】(2020春•金凤区校级期末)已知(1),则(1)的值为 .
【分析】根据题意,求出函数的导数,令,可得(1)(1),变形解可得(1)的值.
【解答】解:根据题意,(1),
其导数(1),
令,得(1)(1),
所以(1),
故答案为:
【名师指导】
1.求函数导数的总原则:先化简解析式,再求导.
2.常见形式及具体求导6种方法
题型2 求切线方程
【例2-1】(2020春•蓝田县期末)曲线在点处的切线方程为
A.B.C.D.
【分析】求出原函数的导函数,得到函数在处的导数,再由直线方程的斜截式得答案.
【解答】解:由,得,
.
曲线在点处的切线方程为.
即.
故选:.
【例2-2】已知函数f(x)=xln x,若直线l过点(0,-1),并且与曲线y=f(x)相切,则直线l的方程为________.
【解析】因为点(0,-1)不在曲线f(x)=xln x上,所以设切点为(x0,y0).又因为f′(x)=1+ln x,所以直线l的方程为y+1=(1+ln x0)x.
所以由eq \b\lc\{(\a\vs4\al\c1(y0=x0ln x0,,y0+1=(1+ln x0)x0,))解得x0=1,y0=0.
所以直线l的方程为y=x-1,
即x-y-1=0.
【跟踪训练2-1】(2020•海东市模拟)已知函数,则曲线在点处的切线的方程为 .
【分析】求出原函数的导函数,得到函数在处的导数,再由直线方程的斜截式得答案.
【解答】解:由,得,
,
则曲线在点处的切线的方程为.
故答案为:.
【跟踪训练2-2】(2020·江西吉安一模)过点P(1,1)且与曲线y=x3相切的直线的条数为( )
A.0 B.1
C.2 D.3
【解析】 当点P为切点时,∵y′=3x2,∴y′|x=1=3,则曲线y=x3在点P处的切线方程为y-1=3(x-1),即3x-y-2=0.当点P不是切点时,设直线与曲线切于点(x0,y0)(x0≠1),则k=eq \f(y0-1,x0-1)=eq \f(x\\al(3,0)-1,x0-1)=xeq \\al(2,0)+x0+1.∵y′=3x2,∴y′|x=x0=3xeq \\al(2,0),∴2xeq \\al(2,0)-x0-1=0,∴x0=1(舍)或x0=-eq \f(1,2),∴过点P(1,1)与曲线y=x3相切的直线方程为3x-4y+1=0.综上,过点P的切线有2条,故选C.
【名师指导】
求曲线过点P的切线方程的方法
(1)当点P(x0,y0)是切点时,切线方程为y-y0=f′(x0)·(x-x0).
(2)当点P(x0,y0)不是切点时,可分以下几步完成:
第一步:设出切点坐标P′(x1,f(x1));
第二步:写出过点P′(x1,f(x1))的切线方程y-f(x1)=f′(x1)(x-x1);
第三步:将点P的坐标(x0,y0)代入切线方程求出x1;
第四步:将x1的值代入方程y-f(x1)=f′(x1)(x-x1)可得过点P(x0,y0)的切线方程.
题型3 求切点坐标
【例3-1】(2020春•大兴区期末)过点作曲线的切线,则切点坐标为
A.B.C.D.
【分析】设切点的坐标为,求得函数的导数,由导数的几何意义可得切线的斜率,再由两点的斜率公式,解方程可得切点.
【解答】解:设切点的坐标为,
的导数为,
可得切线的斜率为,
又切线过,可得,
解得,
则切点为.
故选:.
【跟踪训练3-1】(2020•沈阳三模)过点作曲线的切线,则切点坐标为 .
【分析】由已知结合直线的斜率公式及导数的几何意义即可求解.
【解答】解:因为,
所以,设切点为,,
,根据题意可得,
,即切点坐标.
故答案为:.
【名师指导】
求切点坐标的思路
已知切线方程(或斜率)求切点的一般思路是先求函数的导数,再让导数等于切线的斜率,从而求出切点的横坐标,将横坐标代入函数解析式求出切点的纵坐标.
题型4 由曲线的切线(斜率)求参数取值范围
【例4-1】(2020春•海淀区校级期末)曲线在点处的切线斜率为8,则实数的值为
A.B.6C.12D.
【分析】求得的导数,由导数的几何意义,可得切线的斜率,解方程可得的值.
【解答】解:的导数为,
可得在点处的切线斜率为,
解得.
故选:.
【例4-2】(2020春•渭滨区期末)函数的图象存在与直线平行的切线,则实数的取值范围是
A.,B.,
C.,,D.,,
【分析】易知切线斜率为1,由题意可知,只需的值域中含有1即可.由此构造的不等式,解出的范围.
【解答】解:,.
由题意,只需,有解,则只需的值域中包含1即可.
当时,,显然不符合题意;
当时,的开口向下,在对称轴处取得最大值,
故,即,结合得,即为所求.
故选:.
【跟踪训练4-1】(2020春•未央区校级期末)直线与曲线相切,则的值为 .
【分析】求出原函数的导函数,设直线与曲线相切于,得到函数在处的导数,再由题意列关于与的方程组求解.
【解答】解:由,得,
设直线与曲线相切于,
则.
,解得.
的值为2.
故答案为:2.
【名师指导】
1.利用导数的几何意义求参数的基本方法
利用切点的坐标、切线的斜率、切线的方程等得到关于参数的方程(组)或者参数满足的不等式(组),进而求出参数的值或取值范围.
2.求解与导数的几何意义有关问题时应注意的两点
(1)注意曲线上横坐标的取值范围;
(2)谨记切点既在切线上又在曲线上.
题型5 两曲线的公切线问题
【例5-1】(2020•上饶三模)已知与有相同的公切线,设直线与轴交于点,,则的值为
A.1B.0C.D.
【分析】分别设出切点,然后利用导数表示出切线方程,再利用是公切线,列出方程,求出切点,问题即可获解.
【解答】解:对于,设切点为,因为,故.
故切线方程为:.
即;
对于,设切点为,.
,.
故切线为:,
即.
根据为公切线得:,
解得.
故切线为.
令得.
故选:.
【跟踪训练5-1】(2020•遂宁模拟)若存在,使得函数与在这两函数图象的公共点处的切线相同,则的最大值为
A.B.C.D.
【分析】设公共点为,然后根据公共点处函数值相等、导数值相等,列出关于公共点满足的方程组,将消去,得到关于,的等量关系式,整理成(a)的形式,求函数的最值即可.
【解答】解:设公共点为,,且.
所以,由②得,
解得或(舍.
将代入①式整理得:,
令(a),,
,
令(a)得,,且时,(a).
故(a)在上递增,在上递减.
故(a).故的最大值为.
故选:.
【名师指导】
解决此类问题通常有两种方法:一是利用其中一曲线在某点处的切线与另一曲线相切,列出关系式求解;二是设公切线l在y=f(x)上的切点P1(x1,f(x1)),在y=g(x)上的切点P2(x2,g(x2)),则f′(x1)=g′(x2)=.
原函数
导函数
f(x)=c(c为常数)
f′(x)=0
f(x)=xn(n∈Q*)
f′(x)=nxn-1
f(x)=sin x
f′(x)=cs_x
f(x)=cs x
f′(x)=-sin_x
f(x)=ax
(a>0且a≠1)
f′(x)=axln_a
f(x)=ex
f′(x)=ex
f(x)=lgax
(x>0,a>0且a≠1)
f′(x)=eq \f(1,xln a)
f(x)=ln x (x>0)
f′(x)=eq \f(1,x)
连乘形式
先展开化为多项式形式,再求导
三角形式
先利用三角函数公式转化为和或差的形式,再求导
分式形式
先化为整式函数或较为简单的分式函数,再求导
根式形式
先化为分数指数幂的形式,再求导
对数形式
先化为和、差形式,再求导
复合函数
先确定复合关系,由外向内逐层求导,必要时可换元
相关试卷
这是一份高中数学高考课后限时集训14 导数的概念及运算 作业,共6页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份高中数学高考第14讲 导数的概念及运算(学生版),共6页。试卷主要包含了导数的概念,基本初等函数的导数公式,复合函数的导数等内容,欢迎下载使用。
这是一份高中数学高考第14讲 导数的概念及运算(达标检测)(学生版),共6页。










