初中数学沪科版九年级下册24.6.1 正多边形与圆教学演示课件ppt

这是一份初中数学沪科版九年级下册24.6.1 正多边形与圆教学演示课件ppt，共23页。PPT课件主要包含了图片引入，观察与思考，知识要点，正多边形，各边相等，各角相等，缺一不可，练一练，典例精析，正多边形与圆的关系等内容，欢迎下载使用。

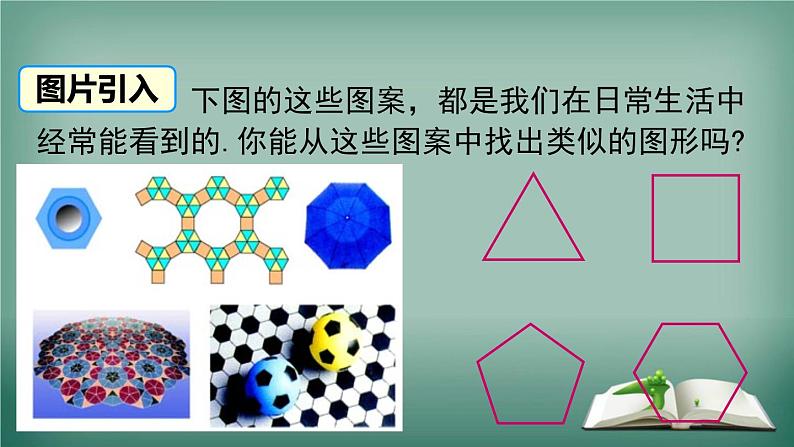
下图的这些图案，都是我们在日常生活中经常能看到的.你能从这些图案中找出类似的图形吗?
正多边形的概念及相关计算
问题1 观察下面多边形，它们的边、角有什么特点？
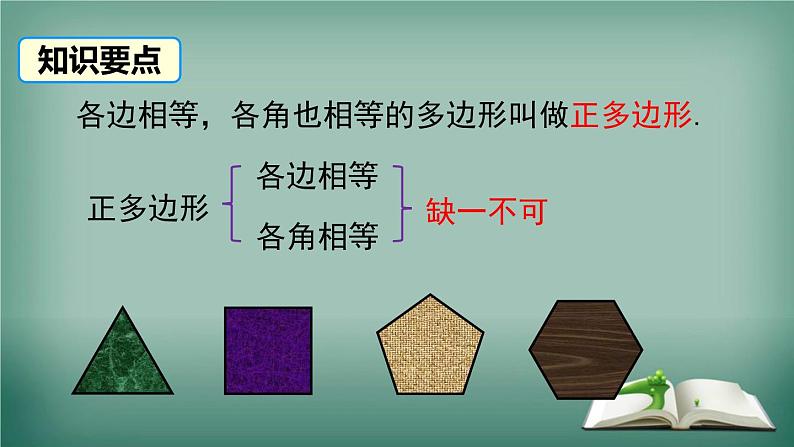
各边相等，各角也相等.
各边相等，各角也相等的多边形叫做正多边形.
问题2 n 边形的内角和为多少？正 n 边形的每个内角的度数如何计算？
问题3 n 边形的外角和为多少？已知正 n 边形的内角为 α 度，如何求 n 的值？
n 边形的外角和为 360°.
正 n 边形的内角为 α 度，则它的外角为 (180 - α) 度.
1. 若一个正 n 边形的每个内角为 144°，则 n = ____.
2. 一个正多边形的内角和为 540°，则这个正多边形的每一个外角都等于 （　　）A．108° B．90° C．72° D．60°
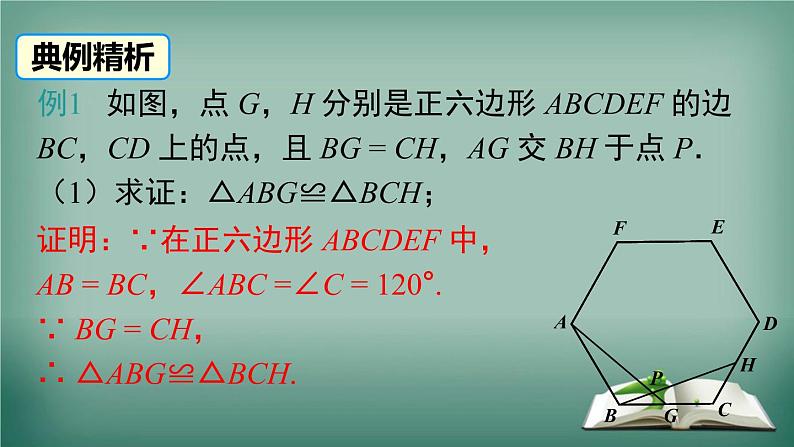
例1 如图，点 G，H 分别是正六边形 ABCDEF 的边 BC，CD 上的点，且 BG = CH，AG 交 BH 于点 P．（1）求证：△ABG≌△BCH；
证明：∵在正六边形 ABCDEF 中，AB = BC，∠ABC =∠C = 120°.∵ BG = CH，∴ △ABG≌△BCH.
解：由（1）知 △ABG≌△BCH，∴∠BAG =∠CBH．∴∠BPG =∠ABG = 120°．∴∠APH =∠BPG = 120°．
（2）求∠APH 的度数．
问题 如图，把 ☉O 进行 5 等分，依次连接各等分点得到五边形 ABCDE. 分别过点 A，B，C，D，E 作☉O 的切线，切线交于点 P，Q，R，S，T，依次连接各交点，得到五边形 PQRST. 则五边形 ABCDE 及五边形 PQRST 是正多边形吗？
探究1 五边形 ABCDE 是正五边形吗？简要说明理由.
② AB____BC____CD____DE____AE.
④ ∠A___∠B___∠C___∠D___∠E.
∵ 顶点 A，B，C，D，E 都在 ☉O 上，
∴ 五边形 ABCDE 是 ☉O 的内接正五边形.
把圆分成 n（n＞2）等份，依次连接各分点所得的多边形就是这个圆的一个内接正 n 边形.
探究2 五边形 PQRST 是正五边形吗？简要说明理由.
五边形 ABCDE 是 ☉O 的内接正五边形.连接 OA，OB，OC.
则∠OAB =∠OBA =∠OBC =∠OCB．
∵ TP，PQ，QR 分别是以点 A，B，C 为切点的 ☉O 的切线，
∴∠OAP =∠OBP =∠OBQ =∠OCQ．
∴∠PAB =∠PBA =∠QBC =∠QCB．
∴ △PAB≌△QBC．
∴ ∠P =∠Q，PQ = 2PA.
∠Q =∠R =∠S =∠T，
QR = RS = ST = TP = 2PA.
∵五边形 PQRST 的各边与 ☉O 相切，
∴五边形 PQRST 是 ☉O 的外切正五边形.
把圆分成 n（n＞2）等份，依次连接过等分点作圆的切线，各切线相交所得的多边形就是这个圆的一个外切正 n 边形.
例2 利用尺规作图，作出已知圆的内接正方形和内接正六边形.
解：（1）内接正方形的作法：
① 用直尺作圆的一条直径 AC；
② 作与 AC 垂直的直径 BD；
③ 顺次连接所得的圆上四点.
则四边形 ABCD 即为所求作的正方形.
再逐次平分各边所对的弧，就可以作出正八边形、正十六边形等.
（2）内接正六边形的作法：
① 用直尺作圆的一条直径 AD；
② 以点 A 为圆心，OA 为半径作圆， 与 ⊙O 交于点 B、F；
④ 顺次连接所得的圆上六点.
则六边形 ABCDEF 即为所求作的正六边形.
③ 以点 D 为圆心，OD 为半径作圆， 与 ⊙O 交与点 C、E.
如果再逐次等分各边所对的弧，就可以作出正十二边形、正二十四边形等.
方法归纳：用等分圆周的方法作正多边形：①用量角器等分圆周；②用尺规等分圆周(特殊正 n 边形).
例3 如图，⊙O 的内接正方形 ABCD，E 为边 CD 上一点，且 DE = CE，延长 BE 交 ⊙O 于 F，连接 FC，若正方形边长为 1，求弦 FC 的长．
解：连接 BD，如图．
在 Rt△CBD 中，
∵∠DBE =∠FCE，∠CFE =∠BDE，∴△DEB∽△FEC.
2. 如图是一枚“八一”建军节纪念章，其外轮廓是一个正五边形，则图中∠1 的大小为______.
1. 如果一个正多边形的一个外角为 30°，那么这个正多边形的边数是 （　　）A．6 B．11 C．12 D．18
3. 如图，正六边形 ABCDEF 内接于半径为 4 的圆，则 B、E 两点间的距离为____.
解析：连接 BE、AE，如图所示. ∵ 六边形 ABCDEF 是正六边形，∴∠BAF =∠AFE = 120°，FA = FE. ∴∠FAE =∠FEA = 30°. ∴∠BAE = 90°. ∴ BE 是正六边形 ABCDEF 的外接圆的直径. ∵正六边形 ABCDEF 内接于半径为 4 的圆，∴ BE = 8.
4.如图，以正六边形 ABCDEF 的边 AB 为边，在形内作正方形 ABMN，连接 MC．求∠BCM 的大小．
解：∵ 六边形 ABCDEF 为正六边形，∴∠ABC = 120°，AB = BC．∵ 四边形 ABMN 为正方形，∴∠ABM = 90°，AB = BM．∴∠MBC = 120° - 90°=30°，BM = BC．∴∠BCM =∠BMC．∴∠BCM = 75°．
5. 如图，已知正五边形 ABCDE，AF∥CD 交 DB 的延长线于点 F，交 DE 的延长线于点 G，求∠G 的度数．
解：∵ ABCDE 是正五边形，∴∠C =∠CDE = 108°，CD = CB.∴∠1 = 36°.∴∠2 = 108° - 36° = 72°.∵ AF∥CD，∴∠F =∠1 = 36°.∴∠G = 180° -∠2 -∠F = 72°.