2023届江淮十校高三第二次联考数学试题含答案

这是一份2023届江淮十校高三第二次联考数学试题含答案，共19页。试卷主要包含了选择题，多选题，填空题，解答题等内容，欢迎下载使用。
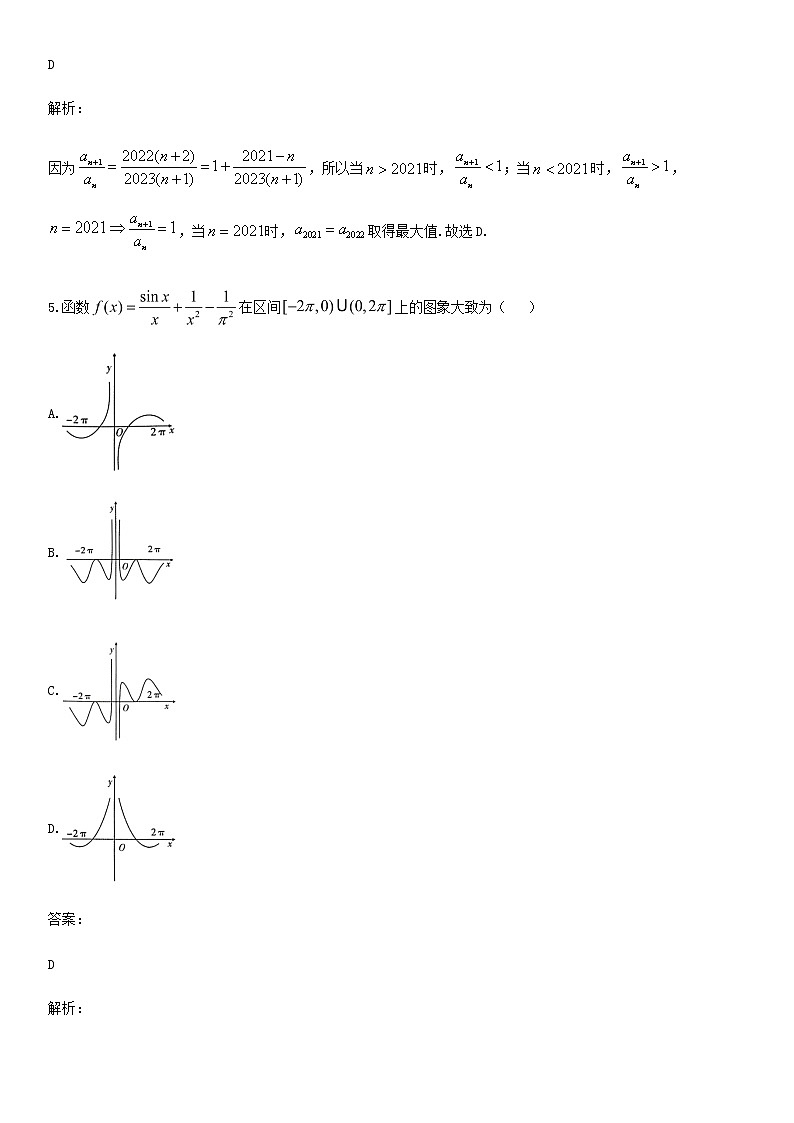
江淮十校2023届高三第二次联考数学试题一、选择题1.若集合，，则（   ）A.B.C.D.答案：C解析：由，得或，又，所以，选C.2.设，则“”是“”的（   ）A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件答案：A解析：即，.而即，，所以选A.3.我们平时听到的乐音不只是一个音在响，而是许多个音的结合，称为复合音.复合音的产生是因为发声体在全段振动，产生频率为的基音的同时，其各部分如二分之一、三分之一、四分之一部分也在振动，产生的频率恰好是全段振动频率的倍数，如，，等.这些音叫谐音，因为其振幅较小，一般不易单独听出来，所以我们听到的声音的函数为.则函数的周期为（   ）A.B.C.D.答案：B解析：由题意，的周期为，的周期为，的周期为.所以的周期为.选B.4.已知数列满足，则当取得最大值时的值为（   ）A.B.或C.D.或答案：D解析：因为，所以当时，；当时，，，当时，取得最大值.故选D.5.函数在区间上的图象大致为（   ）A.B.C.D.答案：D解析：由题意可得是偶函数，排除A,C两个选项，又，当时，，，，当时，，，，所以当时，仅有两个零点.故选D.6.已知向量，，.若在方向上投影向量模长为，则实数为（   ）A.B.C.D.答案：C解析：由，在方向上的投影向量模长为，所以，选C.7.已知实数，，，则（   ）A.B.C.D.答案：B解析：易证对恒成立，当且仅当时等号成立，取，所以，即.又易证对恒成立，当且仅当时等号成立，取，所以，即，综上，选B.8.我国古代数学著作《九章算术》中有如下问题：“今有人持金出五关，前关二税一，次关三而税一，次关四而税一，次关五而税一，次关六而税一，并五关所税，适重一斤.问本持金几何？”其意思为“今有人持金出五关，第关收税金为持金的，第关收税金为剩余金的，第关收税金为剩余金的，第关收税金为剩余金的，第关收税金为剩余金的，关所收税金之和恰好重斤.问原来持金多少？”.记这个人原来持金为斤，设，则（   ）A.B.C.D.答案：C解析：由题意知：这个人原来持金为斤，第关收税金为斤；第关收税金为斤；第关收税金为斤，以此类推可得，第关收税金为斤.第关收税金为斤，所以，即，解得，又由，所以.故选C.二、多选题9.已知函数，则下列结论正确的是（   ）A.导函数为B.函数的图象关于点对称C.函数在区间上是增函数D.函数的图象可由函数的图象向左平移个单位长度，再向上平移个单位长度得到答案：B、C解析：对于A：因为，所以，即选项A错误；对于B：由，，所以，，所以的对称中心坐标为，B正确.对于C：当时，，故在上是增函数，即选项C正确；对于D：因为，所以的图象可由的图象向左平移个单位长度，再向上平移个单位长度得到，即选项D错误.故选BC.10.已知函数是定义在上的奇函数，且.若时，，则下列结论正确的有（   ）A.函数的值域为B.函数图象关于直线对称C.当实数时，关于的方程恰有三个不同实数根D.当实数时，关于的方程恰有四个不同实根答案：A、B、D解析：由，函数周期为.又为奇函数，而时，，即，变形整理得.可得函数图象：由图像可知，函数的值域为且关于对称，选项A、B正确.记，由，所以为偶函数，当时，，当时，.的图象为：又方程有四个不同的根，当时，即直线与函数，，有四个交点，即直线与函数，，有四个交点，数形结合可得，又因为为偶函数，所以，同时时恰有三个交点，选项C错误，D正确.11.已知，均为正实数，下列结论正确的有（   ）A.若，则B.若，则C.若，则D.当且仅当时，取得最大值答案：A、B、C、D解析：其中A：由，所以，A正确.对于B：因为，为正实数，且，所以，当且仅当，时，等号成立，所以B正确.其中C：由，即，由柯西不等式，即，C正确.其中D：因为，均为正实数，所以，令，则，等号成立条件为.D正确.12.已知函数，若在区间上有零点，则的值可以为（   ）A.B.C.D.答案：B、C、D解析：设在区间上零点为，则，所以点在直线上，由，其中为坐标原点.又，记函数，，利用导数可得最小值为，所以，所以选项BCD均满足.三、填空题13.命题：，的否定为________.答案：：，解析：：，14.函数的极大值与极小值的和为________.答案：解析：由，所以或，当或时，，单调递减；当时，，单调递增，所以为极小值，为极大值点，所以.15.已知函数，为直线上一点，过点作函数图象的两条切线，切点分别为，，则的最小值为________.答案：解析：设，.由求导得，则直线，直线，联立方程可得，由在直线上，得，且，即.因而.16.在锐角中，角，，所对的边分别为，，，且满足.若的外接圆的面积为，则三角形面积的取值范围是________.答案：解析：由，所以得，，所以，因为，所以，所以，而，所以.又由的外接圆的面积为，所以外接圆半径，所以，因为为锐角三角形，所以，的面积取值范围为.四、解答题17.已知函数的定义域为集合，关于的不等式的解集为.（1）当时，求；（2）若是的充分条件，求实数的取值范围.答案：见解析解析：由，所以集合；由.（1）由时，不等式为：，即集合；又或，所以或；（2）因为是的充分条件，所以是的子集，或；当时，，满足题意；当时，，所以或得；当时，，所以或得；综上，实数的取值范围为：.18.已知函数（，，）的部分图象如图所示.（1）求函数的解析式；（2）若，其中，求函数的值域.答案：见解析解析：（1）由得：，当时，，，又，所以，又（舍去）；当时，，，又，所以，又，所以，.（2），，又，所以，，，即函数的值域为.19.年是合肥一六八中学建校周年，学校届时将举行周年校庆活动，其中会建立校史展览馆并向各界校友及友好人士展出一六八中学自建校以来的大事记.已知展览馆的某一部分平面图如图所示，的长为米，点到轴和轴的距离分别是米和米，其中边界是函数图象的一部分，前一段是函数图象的一部分，后一段是一条线段，现要在此处建一个陈列馆，平面图为直角梯形（其中、为两个底边）.（1）求函数的解析式；（2）求梯形面积的最大值.答案：见解析解析：（1）.（2）设点，所以，，所以梯形的面积为，设，令，，所以在单调递增，单调递减，所以，即时，梯形面积的最大值为.20.在中，角，，的对边分别是，，，且向量与向量共线.（1）求角；（2）请从条件①、条件②、条件③这三个条件选择一个作为已知，使得存在且唯一确定，并求边上中线的长.条件①：，；条件②：，；条件③：，.答案：见解析解析：（1）由向量与向量共线得：，所以，又因为，所以，所以，又，所以；（2）由①可知：，所以，或，不唯一确定（舍去）；由②可知：，又，所以，即或，不唯一确定（舍去）；由③可知：，，，，，所以.21.设各项均为正数的数列满足.（1）若，求数列的通项公式；（2）在（1）的条件下，设，数列的前项和为，求证：.答案：见解析解析：由得：因为数列为正项数列，所以，所以.（1）若，则，又当时，，所以.（2）由（1）知，所以，所以，不等式成立，所以，所以，所以，所以，因为，仅在时取等号，所以，即结轮成立.22.已知函数.（1）若时，函数恰好有一个零点，求的最大值；（2）讨论函数的零点个数.答案：见解析解析：（1）因为，，所以，因为，所以在，，所以，又当时，；当时，；所以，所以，所以.设，所以，所以在，，所以，所以的最大值为.（2），所以，当时，在恒成立，在，又当时，；当时，；所以，函数在只有一个零点；当时，由得方程有两个根，分别为，且，所以在，，，即为函数的极大值，为函数的极小值，因此主要讨论极值与零的大小，又，，设，，所以，在，所以，所以在区间内没有零点，又，而，所以在上有一个零点；综上所述：在上有一个零点.