




- 2023怀化高二上学期期末考试英语试题含解析 试卷 0 次下载
- 2023怀化高二上学期期末数学试题含解析 试卷 0 次下载
- 2023怀化高二上学期期末考试政治试题含答案 试卷 0 次下载
- 2023怀化高二上学期期末考试地理试题含解析 试卷 0 次下载
- 2023怀化高二上学期期末考试历史试题含解析 试卷 0 次下载
2023怀化高二上学期期末数学试题含解析
展开怀化市2022年下期期末考试试卷
高二数学
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 直线的倾斜角为()
A. B. C. D.
2. 已知椭圆一个焦点坐标为,则的值为()
A. 1 B. 3 C. 7 D. 9
3. 已知数列满足,,则数列的前2023项的乘积为()
A. B. 1 C. 2 D. 3
4. 在平行六面体中,若,且与所成的角均为,则()
A. 5 B. C. D.
5. 双曲线的一个焦点与抛物线的焦点重合,则双曲线离心率为()
A. B. C. 2 D. 3
6. 如图,在直三棱柱中,,则直线与直线夹角的余弦值为()
A. B. C. D.
7. 已知椭圆的左、右焦点分別为,上顶点为,且,点在上,线段与交于.则直线的斜率为()
A. B. C. D.
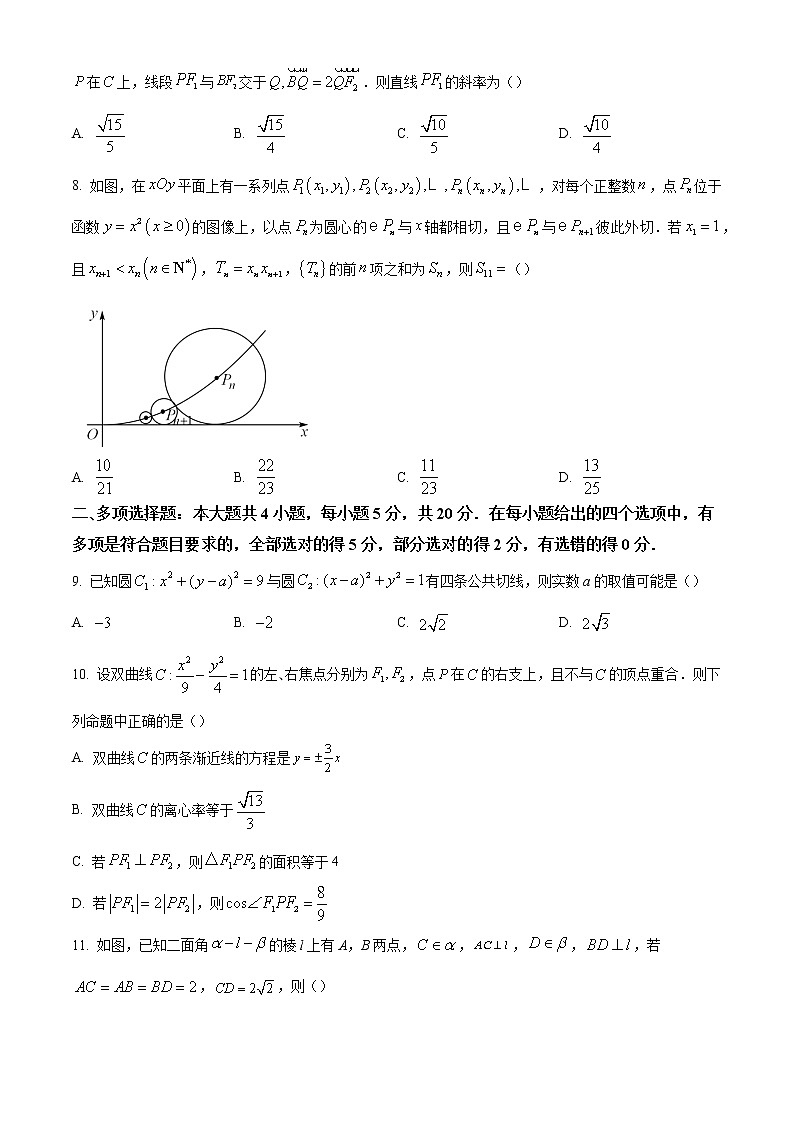
8. 如图,在平面上有一系列点,对每个正整数,点位于函数的图像上,以点为圆心的与轴都相切,且与彼此外切.若,且,,的前项之和为,则()
A. B. C. D.
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项是符合题目要求的,全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 已知圆与圆有四条公共切线,则实数a的取值可能是()
A. B. C. D.
10. 设双曲线的左、右焦点分别为,点在的右支上,且不与的顶点重合.则下列命题中正确的是()
A. 双曲线的两条渐近线的方程是
B. 双曲线的离心率等于
C. 若,则的面积等于4
D. 若,则
11. 如图,已知二面角的棱l上有A,B两点,,,,,若,,则()
A. 直线AB与CD所成角余弦值为45°
B. 二面角的大小为60°
C. 三棱锥的体积为
D. 直线CD与平面所成角的正弦值为
12. “提丢斯数列”是18世纪由德国数学家提丢斯给出的,具体如下:取0,3,6,12,24,48,96,192,…这样一组数,容易发现,这组数从第3项开始,每一项是前一项的2倍,将这组数的每一项加上4,再除以10,就得到“提丢斯数列”:0.4,0.7,1.0,1.6,2.8,5.2,10.0,…,则下列说法中正确的是()
A. “提丢斯数列”是等比数列
B. “提丢斯数列”的第99项为
C. “提丢斯数列”的前31项和为
D. “提丢斯数列”中,不超过20的有9项
三、填空题:本题共4小题,每小题5分,共20分
13. 等比数列的前项和为,则的值为_____.
14. 如图,已知正方体中,分别为中点,,则到平面的距离是__________.
15. 已知抛物线的准线方程为,在抛物线C上存在A、B两点关于直线对称,设弦AB的中点为M,O为坐标原点,则的值为___________.
16. 已知双曲线方程,其左、右焦点分别是,已知点坐标为,双曲线上点满足,设的内切圆半径为.则__________;__________.
四、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.
17已知等差数列满足,.
(1)求数列的通项公式;
(2)设等比数列各项均为正数,其前项和,若,,求.
18. 已知抛物线的准线方程是是抛物线焦点.
(1)求抛物线焦点坐标及其抛物线方程:
(2)已知直线过点,斜率2,且与抛物线相交于两点,求.
19. 如图1,在直角梯形中,,且.现以为一边向梯形外作正方形,然后沿边将正方形折叠,使,如图2.
(1)求证:平面;
(2)求直线和平面所成的角的正弦值.
20. 已知数列的首项,且满足.
(1)求证:数列为等比数列;
(2)若,数列前项的和为,求.
21. 如图,在直角梯形中,,,平面,,.
(1)求证:;
(2)在直线上是否存在点,使二面角的大小为?若存在,求出的长;若不存在,请说明理由.
22. 已知点,点分別为椭圆的左、右顶点,直线交曲线于点是等腰直角三角形,且.
(1)求的方程:
(2)设过点的动直线与相交于,两点.当以为直径的圆过坐标原点时,求直线的斜率.
2023怀化高一下学期期末数学试题含解析: 这是一份2023怀化高一下学期期末数学试题含解析,文件包含湖南省怀化市2022-2023学年高一下学期期末数学试题含解析docx、湖南省怀化市2022-2023学年高一下学期期末数学试题原卷版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。
2022-2023学年湖南省怀化市高一上学期期末数学试题含解析: 这是一份2022-2023学年湖南省怀化市高一上学期期末数学试题含解析,共12页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年湖南省怀化市高二上学期期末数学试题 (解析版): 这是一份2022-2023学年湖南省怀化市高二上学期期末数学试题 (解析版),共19页。试卷主要包含了 直线的倾斜角为等内容,欢迎下载使用。











